Авиастроение является одним из наиболее высокотехнологичных секторов мировой экономики, который бурно развивается последнее десятилетие, при этом претерпевая серьезные изменения, т.к. быстро меняются не только технологии, но и ситуация на мировом рынке и природа конкуренции внутри отрасли. Изменяется характер отношений на глобальном рынке: ведущие производители усиливают свои позиции, становясь системными интеграторами, которые координируют бизнес-процессы поставщиков путем аутсорсинга, а поставщики берут на себя ответственность за управление всем жизненным циклом своих частей изделия, от проектирования до производства по заданной программе. Кроме того, в связи с увеличением роли информации, знаний и информационных технологий требуется учитывать влияние всё большего количества агентов рынка (заказчики, новые участники рынка и т.д) [2]. Поэтому системный анализ конкуренции в авиационной промышленности (АП) является исключительно актуальной проблемой.
В исследовании отраслевой конкуренции сегодня нуждается каждый участник АП независимо от масштабов бизнеса, т.к. важно правильно оценивать ситуацию во внешней и внутренней среде компании для формирования собственной конкурентной стратегии, поэтому конкурентный анализ (КА) как специальный вид системных исследований выполняется, как правило, в интересах одного из участников рынка с использованием всей имеющейся на данный момент информации.
Постановка задачи
Для исследования конкуренции в секторе объектов авиационной техники (ОАТ) были проанализированы существующие модели и методы олигополии (т.к. в секторе ОАТ, как правило, несколько участников, влияющих на ситуацию на рынке) и выявлено, что известные теории и модели в новых условиях, в частности – при конкурентном анализе ОАТ, не гарантируют достоверных результатов, т.к. описывая поведение сложной системы в целом, основываются на принципах полной рациональности действий всех участников, не учитывают динамику развития рынков высокотехнологичной продукции АП, а также параллельность процессов во времени и их взаимосвязь. Поэтому потребовалось разрабатывать другие модели и методы с использованием фрактальной алгебры и графодинамики.
Конкуренция в сегменте ОАТ представлена как сложная система (СС), подсистемами данной СС (рис. 1) в соответствии с модифицированной моделью конкуренции [2] на основе модели М. Портера [6] являются основные конкуренты на рынке АП F1, новые участники рынка F2 , производители товаров-заменителей F3 , поставщики комплектующих и компонент F4, заказчики авиационной техники F5 и комплементоры F6 [9] (неявные участники рынка, предлагающие свои продукты и/или услуги и увеличивающие или уменьшающие привлекательность определенных продуктов на рынке ЛА, таким образом, влияющие на положение основных игроков). Элементами СС являются компании-агенты различного типа для каждой из рассматриваемых подсистем, информированность которых о конкурентах и внешней среде моделируется регулятором. Структура данной СС представляет собой фрактальный нагруженный граф 
.
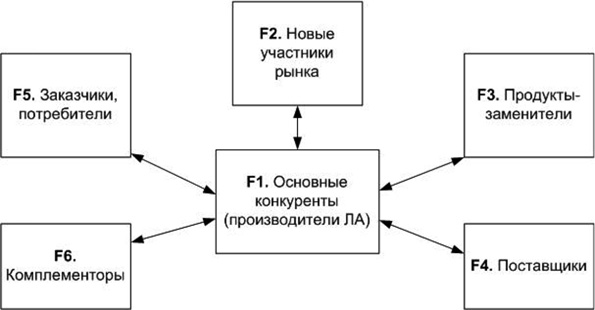
Рис. 1. Основные подсистемы СС глобальной конкуренции
Описание модели регулятора
С целью построения агентной модели СС конкуренции в секторе ОАТ разработаны модели поведения игроков на олигополистическом рынке (модели Курно, Бертрана, Штакельберга и Суизи) на основе модели регулятора (рис. 2), где V1, V2 – агенты, R – регулятор. Регулятором называют агента, отвечающего за правила игры и динамическое равновесие системы (демонополизацию рынка), а так же «общее знание» или «симметричное общее знание»1. Использование регулятора позволяет объединить иерархию представлений агентов друг о друге в едином «общем знании» и представить модель принятия решений агентами в виде рефлексивной игры, в которой каждый агент моделирует в рамках своих представлений поведение конкурентов, ожидая от них определенных действий.
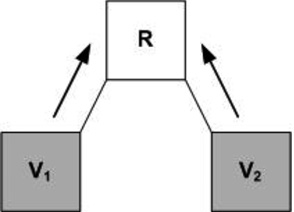
Рис. 2. Модель регулятор-агенты
В основе этой модели лежит точка динамического равновесия, когда при заданных правилах игры система приходит к состоянию динамического равновесия. Эта точка известна как равновесие по Нэшу [1]. В работе эта точка для каждой из рассмотренных моделей находится посредством алгоритмов, основанных на взаимодействии регулятора и агентов.
В модели Курно [10] агенты принимают решение относительно объемов производства одновременно, исходя из своих предположений о решениях, принятых другими игроками. В упрощенной модели на рынке действуют только два агента, и каждый агент принимает цену и объем производства конкурента неизменными, а затем принимает свое решение. Каждый из двух продавцов допускает, что его конкурент всегда будет удерживать свой выпуск стабильным. В модели предполагается, что продавцы не узнают о своих ошибках. Фактически же эти предположения продавцов о реакции конкурента, очевидно, изменятся, когда они узнают о своих предыдущих ошибках.
В модели Бертрана [3] на рынке действуют два агента, продукт производится однородный, целью каждой фирмы является максимизация прибыли. Кроме того, отсутствуют соглашения фирм друг с другом; агенты назначают цены одновременно так, что каждая не может прогнозировать реакцию конкурента на сделанный ею самой выбор.
В модели Штакельберга рассматривается ситуация ассиметричной конкуренции агентов, осуществляющих стратегическое взаимодействие по принципу «лидер – последователь». Модель Штакельберга базируется на следующих предпосылках: фирмы производят однородную продукцию; на рынке присутствует фирма-лидер, на объемы производства которой ориентируются все остальные фирмы (фирмы-последователи), определяя свои объемы производства, исходя из критерия максимизации прибыли. Фирма-лидер обладает полной информацией относительно рынка и действующих на нем фирм, ей известно, что фирмы-последователи определяют свой объем производства, исходя из ее объема производства, и знает функции наилучшей реакции фирм-последователей на свои действия. Фирмы-последователи обладают полной информацией о рыночном спросе и при определении оптимальных объемов производства предполагают, что объемы производства всех остальных фирм останутся неизменными.
Модель Суизи модель исходит из предположения, что конкуренты поддержат любое снижение цены одного из агентов, но будут игнорировать ее повышение.
Применение операций фрактальной алгебры
Структура конкуренции как сложной системы описывается фрактальными графами, которые определяются аксиоматически, посредством применения операций фрактальной алгебры [6] к исходному графу G. Исходный граф G (рис. 1) представляет собой упорядоченную пару (V, E), где V – множество элементов системы (агентов рынка), E – ребра (взаимодействия между ними).
Фрактальный граф получен из исходного графа 
с помощью применения операций фрактальной алгебры (подразбиения, копирования и соединения) (рис. 3).
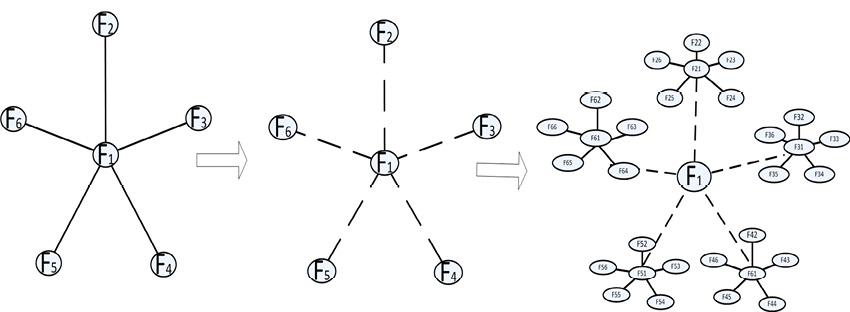
Рис. 3. Последовательность преобразований структуры СС из исходного графа конкуренции
Важнейшим свойством полученной структуры СС как фрактального графа является инвариантность внутренней структуры (рис. 4): подграф подобен графу, т.к. фрактальные графы самоподобны. Таким образом, устанавливается масштабирование: задавая тип отношений между агентами на первом уровне иерархии, можно распространить их на все другие уровни (в данном случае количество уровней иерархии модели определяется степенью её детализации, выбираемой ЛПР, т.е. заказчиком, в чьих интересах проводится исследование конкуренции в отрасли). Кроме того, использование модели регулятора позволяет осуществлять информационное управление, воздействовать на структуру информированности агентов с целью установления информационного равновесия.
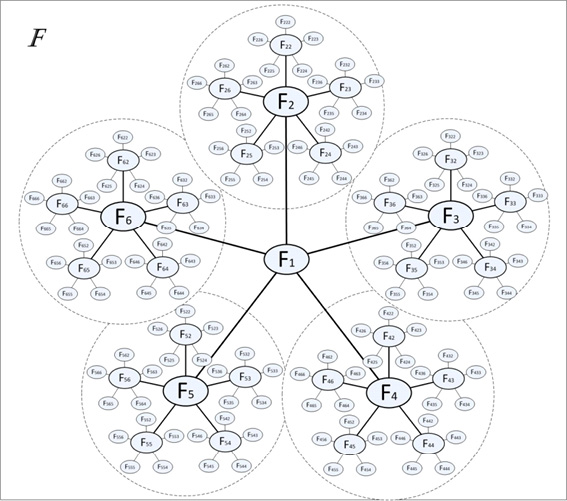
Рис. 4. Структура СС конкуренции в секторе ОАТ в виде фрактального нагруженного графа
Этапы построения целевой функции агента и регулятора
Разработан метод синтеза целевых функций агентов и регулятора. В общем случае информированность агента моделируется структурой информированности агента в виде графа. При увеличении информированности агента увеличивается его пространство принятия решений. Информированность агента будем моделировать посредством графа, где каждой вершине ставится в соответствие подагент, владеющий частью информации. Таким образом, реализуется отношение агент-подагент (целое-часть), а целевая функция агента состоит из базовых целевых подфункций, которые имеет смысл представлять в виде базовых графов. Здесь вершинами являются функции, которые соединяются с вершинами аргументов, где P – модель ценообразования, V – модель объема производства (корректировка объема), S – модель взаимодействия (с конкурентами и другими агентами рынка), задание поведения агента, П – продукционная модель знаний о других агентах (ординарная, дифференцированная).
Модель самоорганизации системы
Конкуренция как самоорганизующаяся система со сложной структурой подразделяется на стадии стабильного развития и стадии переходов, за которыми следует стадия стабильного развития (рис. 5). В рамках жизненного цикла процессы развития системы подразделяются на итерации, каждая из которых состоит из стадии стабильного развития и стадии перехода [4]. За итерацией следует следующая итерация.
На стадии стабильного развития на систему воздействуют внешние факторы (например, изменяются или совершенствуются бизнес процессы в компаниях-агентах рынка), поэтому вносятся изменения. По истечению некоторого времени могут изменяться её параметры, рынок развивается, т.е. добавляются новые агенты [8].
Каждая стадия 
характеризуется: 1) внешними воздействиями; 2) процессами (адаптация, изменение параметров, бифуркация, самоорганизация); 3) внутренними механизмами, управляющими процессами. Коэффициент сложности зависит от количества вершин в графе, с увеличением количества вершин – увеличивается сложность графа. Коэффициент сложности можно менять в зависимости от количества агентов на рынке.
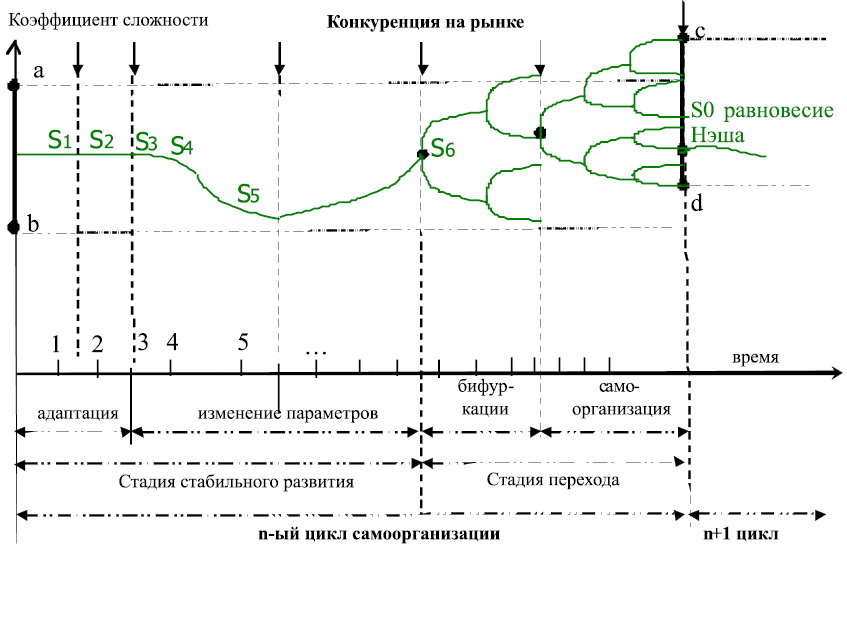
Рис. 5. Стадии самоорганизации CC конкуренции, Si – стратегия
Стадии стабильного развития соответствует определенный временной период, в течение которого нет качественных изменений. Плотность рынка меняется во времени, и изменяется точка равновесия (от N – количество агентов). Изменение параметров показывает договоренности между агентами различных типов (поставщики, заказчики и др.).
Коэффициент сложности выражен через информативность. Целевая функция моделируется фрактальным графом – f(Cni+1).
Общий подход к построению модели самоорганизующейся системы
Коэффициент сложности (упорядоченности) графа g = (V,E) определяется формулой:
где ρ (vi) – степень вершины, определяемая количеством ребер из множества E, инцидентных вершине vi∈V; k – число вершин в графе g, k = |V|.
При равных k коэффициент Ω больше для графов с большим количеством ребер. Коэффициент Ω может учитывать другие свойства графа.
Конфигурацией С фрактоида [7] называется двойка:
С = (g,γ)∈ G×Σ*, 345 g∈G, γ∈Σ*,
где g ∈G – класс фрактального графа, Σ*– множество всех цепочек алфавита.
Фрактальная графодинамическая система формируется семейством фрактоидов:
где ƒn, ƒi+1, ƒi – семейство фрактоидов; n – размер семейства фрактоидов. Семейство фрактоидов формирует хаотический аттрактор размерностью n; f(Ci+1) – функция пригодности конфигурации Ci+1 вычисляется на каждом такте фрактоида.
Семейство фрактоидов формируется таким образом, что для каждого последующего класса фрактоида, значение конфигурации предыдущего является исходным, то есть фрактоиды вложены друг в друга.
Если класс исходного графа фрактоида и тип преобразования совпадают, то такт срабатывания фрактоида не изменяет класс исходного графа, используя множество правил p∈P.
Целостная фрактоидная модель самоорганизации записывается фрактоидом размерности n =2.
,
[(v∈g) ↔ (v’∈g’), (v∈g) ÷ (v’∈g’)]], T),
где S: M→ P – функция выбора правил; M – множество моделей олигополии: Курно, Бертрана, Штакельберга, Суизи; P – множество правил построения моделей равновесия; f(Cni+1) – синтезированная целевая функция агентов и регулятора, и коэффициент b< Ω < a будет характеризовать степень информированности рынка; g0 – начальный граф высоты n=2; Т – тип дерева информированности; M(S) – функция выбора правил из всех правил, которые есть в моделях, каждое правило соответствует шагу;
Правила построения деревьев применяются к синтезу целевых функций.
Заключение
Таким образом, было проведено исследование конкуренции в секторе ОАТ и выявлено, что существующие модели и методы олигополии в новых условиях, в частности – при конкурентном анализе ОАТ, не гарантируют достоверных результатов, поэтому требуется разрабатывать новые модели и методы конкурентного анализа с использованием фрактальной алгебры и графодинамики.
Конкуренция в секторе ОАТ предоставлена сложной самоорганизующейся системой, подсистемами которой являются основные конкуренты, поставщики, заказчики продукции, новые участники рынка, производители товаров-заменителей и комплементоры.
Элементами СС являются компании-агенты различного типа для каждой из рассматриваемых подсистем, информированность которых о конкурентах и внешней среде моделируется с помощью регулятора. Структура данной СС представляет собой фрактальный нагруженный граф. Стадии самоорганизации данной СС характеризуются коэффициентом сложности, отражающим изменения во взаимодействии агентов и в их информированности.
Построена агентная модель СС конкуренции в секторе ОАТ, включающая в свой состав модели поведения игроков на олигополистическом рынке на основе модели регулятора, которая позволяет объединить иерархию представлений агентов друг о друге в едином «общем знании» и представить модель принятия решений агентами в виде рефлексивной игры.
Разработан метод синтеза целевых функций агентов и регулятора, в котором информированность агента моделируется структурой информированности в виде графа, есть возможность учесть различные виды информации, а целевая функция агента состоит из базовых целевых подфункций (модели ценообразования, корректировки объема производства, взаимодействия с другими агентами и знаний о них).
С использованием разработанных моделей была построена целостная фрактоидная модель самоорганизации СС конкуренции, позволяющая исследовать все виды взаимодействий в секторе ОАТ, моделировать различные сценарии развития данного сектора экономики и формировать рекомендации по выбору конкурентной стратегии компании на данном рынке.
Библиографическая ссылка
Бабенко Е.А., Семенов А.С. АНАЛИЗ РЫНОЧНОЙ КОНКУРЕНЦИИ В АВИАЦИОННОЙ ОТРАСЛИ С ИСПОЛЬЗОВАНИЕМ ФРАКТАЛЬНЫХ МОДЕЛЕЙ // Современные наукоемкие технологии. – 2013. – № 9. – С. 140-145;URL: https://top-technologies.ru/ru/article/view?id=33248 (дата обращения: 21.11.2024).