Под гибридной фрактальной структурой будем понимать фрактальную структуру из двух или более простых фракталов с разными генераторами [1,2]. Гибридную фрактальную структуру, составленную из упорядоченных в пространстве локальных фракталов, будем считать детерминистической гибридной фрактальной структурой. Формирование детерминистических гибридных фрактальных структур проводится путем вложения по определенному алгоритму простых фракталов с разными генераторами в пространственные ячейки структурированного пространства методами комбинаторного или итерационного модулярного дизайна [3-24].
Сформулируем общие принципы формирования детерминистических гибридных фрактальных структур в 2D-пространстве [14, 15]:
1) принцип использования предварительно структурированного (сеточного) пространства,
2) принцип отбора мономодулярных одногенераторных фрактальных структур с близкими локальными размерностями по критериям совместимости на границе и внутри пространственных ячеек,
3) принцип выбора гибридных фракталов с минимальными периодами идентичности и максимальной симметрией.
Введем следующее символьное обозначение для детерминистической гибридной фрактальной структуры в 2D-пространстве:
MGF22 {(ai GenFi; bj GenFj) (G20)i (CP)}[(G22), (a, b), (Dim)].
Здесь: MGF22 – наименование двумерной дважды периодической мультифрактальной гибридной структуры, GenFi и (G20)i – генератор i-го простого фрактала и его локальная симметрия, CP – код упаковки простых фракталов или последовательность их чередования в двух кристаллографически независимых направлениях, G22 – группа симметрии двумерной дважды периодической гибридной структуры (), Σai = a и Σbi = b – количества ячеек 2D-пространства, определяющих периоды идентичности структуры, Dim – фрактальная размерность.
Для 2D-пространства структурированность достигается разбиением его на одинаковые ячейки [0,1; 0,1] – интервалы существования мономодулярной точечной фрактальной структуры [16-18]. Тогда будем учитывать, что каждая простая фрактальная структура формируется в результате бесконечной итерации генератора, заданного внутри этих ячеек, инъективным способом и не выходит за ее границы, но имеет общие элементы.
Гибридность фрактальных структур в 2D-пространстве определяется наличием в них двух и более простых фракталов с разными генераторами, занимающими граничащие друг с другом ячейки. В качестве примера классических точечных фрактальных структур могут быть, в частности, итерационная последовательность точек ICр(1/2) (Dim ICр = 0,50, симметрия группы G10 = 1), канторово множество точек CMр(1/3) (Dim CMр = 0,631, симметрия группы G10 =
), итерационная последовательность линий ICl(1/2) (Dim ICl = 1,50, симметрия группы G20 = 1), канторово множество точек CMl (1/3) (Dim CMl = 1,631, симметрия группы G20 =
) и треугольная кривая Коха СК(4/3) (Dim CК = 1,26, симметрия группы G10 = 1). В качестве дополнений к ним могут использоваться отрезок линии L (Dim L = 1, симметрия группы G10 =
) и квадрат Sq (Dim Sq = 2, симметрия группы G20 = 4 mm). Перечислим некоторые формально возможные варианты гибридных фракталов из перечисленных выше структур с одним генератором в виде последовательности их чередования (кодами упаковки) внутри периодов идентичности a и bmin= 1:
1) (ICр(+), CMр) – (CMр, CMр) – (ICр(-), CMр), (a,b) = (3,1),
2) (ICр(+), CMр) – (CMр, CMр) – (L, CMр) – (CMр, CMр) – (ICр(-), CMр), (a,b) = (5,1),
3) (ICр(+), CMр) – (L, CMр) – (CMр, CMр) – (L, CMр) – (ICр(-), CMр), (a,b) = (5,1),
4) ICl(+) – CMl – ICl(-), (a,b) = (3,1),
5) ICl(+) – CMl – Sq – CMl – ICl(-), (a,b) = (5,1),
6) ICl(+) – Sq – CMl – Sq – ICl(-), (a,b) = (5,1),
7) (ICр(+), CMр) – (CK, CMр) – (ICр(-), CMр), (a,b) = (3,1),
8) (ICр(+), CMр) – (CK, CMр) – (L, CMр) – (CK, CMр) – (ICр(-), CMр), (a,b) = (5,1),
9) (ICр(+), CMр) – (L, CMр) – (CK, CMр) – (L, CMр) – (ICр(-), CMр), (a,b) = (5,1),
10) (ICр(+), CMр) – (CK, CMр) – (CMр, CMр) – (CK, CMр) – (ICр(-), CMр), (a,b) = (5,1),
11) (ICр(+), CMр) – (CMр, CMр) – (CK, CMр) – (CMр, CMр) – (ICр(-), CMр), (a,b) = (5,1),
12) (ICр(+),CMр)– (CMр,CMр)– (L,CMр)– (CK,CMр)– (L,CMр)– (CMр,CMр)– (ICр(-),CMр), (a,b)=(7,1),
13) ICl(+) – CKsq – ICl(-), (a,b) = (3,1),
14) ICl(+) – Sq – CKsq – Sq – ICl(-), (a,b) = (5,1),
15) ICl(+) – CKsq – Sq – CKsq – ICl(-), (a,b) = (5,1),
16) ICl(+) – CKsq – CMl – CKsq – ICl(-), (a,b) = (5,1),
17) ICl(+) – CMl – CKsq – CMl – ICl(-), (a,b) = (5,1),
18) ICl(+) – CMl – Sq – CKsq – Sq – CMl – ICl(-), (a,b)=(7,1).
Выше с помощью символов + и – учтена асимметрия фракталов ICр(1/2) и ICl (1/2) относительно геометрического центра интервала их существования.
Соответствующие этим последовательностям гибридные мультифрактальные структуры MGF22 будут иметь следующие симметрийные характеристики G20 и G22: mm2 и pmm2 (структуры 1–6), m и pm (структуры 7–18).
Размерности гибридных фрактальных структур определяются через известные размерности генераторов простых мономодулярных фракталов следующим образом:
Dim(MGF22 {ai GenFi; bj GenFj} == a–1 Σai DimGenFi + b–1 Σbj DimGenFj.
Изображения элементарной ячейки предфракталов 3-го поколения с кодами упаковки (1) и (10) представлены на рисунке.
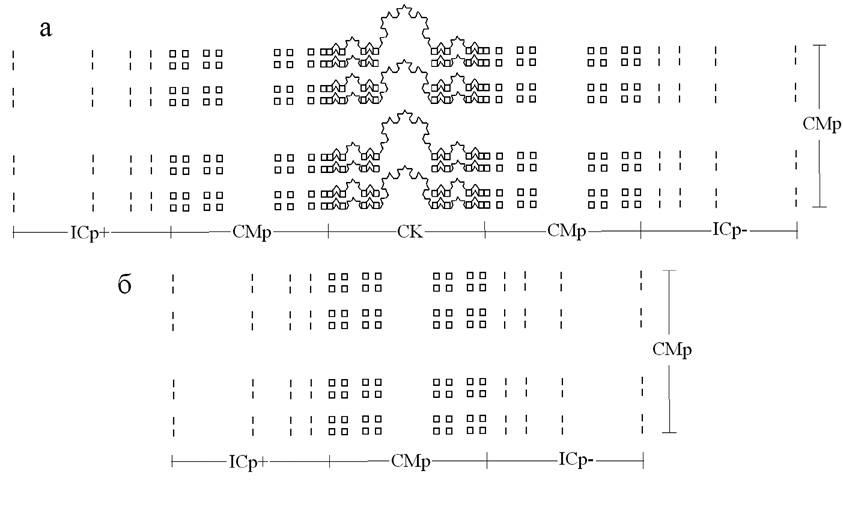
Изображения элементарной ячейки предфрактала 3-го поколения MGF22{(2GenICp, 2GenCM, GenCK; GenCM) (m, mm2, m; mm2) (CP)}[(pm), (5, 1)(Dim=1,334)] (а) и MGF22{(2GenICp, GenCM; GenCM) (m, mm2; mm2) (CP)}[(pmm2), (3, 1)(Dim=1,173)] (б)
Можно также допустить возможность существования некоторых кентавроподобных гибридных структур MGKF22, включающих переходные структуры Tr(F1*F2) – слои квазинепрерывного перехода от одного простого фрактала F1 к другому F2. В частности, такими структурами для гибридов 2D-пространства могут быть переходные структуры Tr(L*CK) (Dim=1) и Tr(ICp*CMp) (Dim=0). В этом случае максимально симметричные кентавроподобные гибридные структуры с минимальными периодами идентичности могут быть получены на основе тех же перечисленных выше 18-ти последовательностей простых фракталов. Учитывая, что переходные структуры не обладает фрактальными свойствами, размерности всех кентавроподобных фрактальных структур на основе перечисленных выше 18-ти будут ниже.
Отметим, что все полученные гибридные фрактальные структуры MGF22, симметрия которых описывается плоскими группами класса G22, могут быть прообразами новых гибридных структур. В частности, при использовании одной трансляции (τ3) непрерывной группы Tt1,t2,τ3 в ортогональном направлениии к дискретным трансляциям t1 и t2 из представленных выше структур могут быть получены новые планарные фракталы вида MGF32. Симметрия образов структур этих фракталов будет описываться одной из 3D-групп симметрии слоев G32 (например, pmmm, pmm2 или p4mm). Обозначения всех 2D- и 3D-групп симметрии приведены в соответствии с обозначениями, принятыми в [25].
В данной работе были проанализированы вероятные гибридные фрактальные структуры 2D-пространства как возможные аппроксиманты поверхности композиционных покрытий (КП) и сайз-распределения наноразмерных объектов на ней. В соответствии с концепцией синергизма свойств фаз твердой и смазочной компонент КП [26-29] в процессе трибоконтакта с сопряженной поверхностью износ более пластичной смазочной компоненты существенно снижается за счет ее специфического взаимодействия с макродефектами и межкристаллитным пространством фаз твердой компоненты [29]. Синергическая модель, описывающая трибологические свойства поверхности КП, основана на одновременном учете параметра наноструктурности и параметра, характеризующего квазифрактальный характер конфигурации межфазных границ [30]. Экспериментально установлено [29, 31-36], что для КП разного фазового состава сумма этих параметров может принимать существенно большие значения (от 0,03 до 0,08) и характеризует объемную долю наночастиц (или микрочастиц) фаз твердых компонент КП и контр-тела, которые могут находиться в зоне трибоконтакта. Сайз-распределения, полученные на основе анализа гибридных фрактальных структур, включающих локальную структуру F(ICp), для предфракталов 3-го поколения характеризуются интервалом значений (0,2…0,8)r0 нм (при размере структурного элемента r0 = 0,5 нм параметр пространственной ячейки 5 нм). Если сайз-распределения получены на основе анализа гибридных фракталов, включающих структуру F(CMp), то для предфракталов 3-го поколения имеем интервал значений (0,3…2,7)r0 нм (при r0 = 0,5 нм параметр пространственной ячейки 15 нм). Следовательно, если структурные элементы предфракталов представляют собой нанообъекты с размером порядка 0,5 нм, то периоды идентичности их гибридных структур (параметры элементарной ячейки) могут принимать значения от 15 до 135 нм.
Таким образом, сформулированы общие принципы формирования, предложено символьное описание и получены некоторые из формально возможных детерминистических гибридных фрактальных структур в 2D-пространстве.
Работа выполнена при частичной финансовой поддержке Министерства образования и науки РФ, соглашение № 14.U01.21.1078.
Библиографическая ссылка
Иванов В.В. ФОРМИРОВАНИЕ И СИМВОЛЬНОЕ ОПИСАНИЕ ДЕТЕРМИНИСТИЧЕСКИХ ГИБРИДНЫХ ФРАКТАЛЬНЫХ СТРУКТУР В 2D-ПРОСТРАНСТВЕ // Современные наукоемкие технологии. – 2013. – № 9. – С. 89-92;URL: https://top-technologies.ru/ru/article/view?id=33238 (дата обращения: 21.11.2024).