Для расчета и проектирования винтовых устройств необходимо располагать данными о характере функциональной связи между их параметрами и кинематическими элементами движения транспортируемого материала и отдельных их частиц. В транспортерах с рабочим органом в виде винтовой поверхности, у которых перемещение частиц материала происходит не только в аксиальном, но и в перпендикулярном к нему направлении, т.е. частица совершает движение на поверхности рабочего органа транспортера по кривой линии.
Рассмотрим случай когда имеется транспортер с рабочим органом в виде винтовой поверхности и с образующими, перпендикулярными к оси рабочего органа. При этом будем считать, что образующая рабочего органа неподвижна, а спирально-винтовая поверхность вращается вокруг своей оси с постоянной угловой скоростью ω. Если в начальный момент времени частица материала находится на поверхности кольца, то через некоторый отрезок времени она окажется затянутой силой трения, возникающей между частицей и спиральной поверхностью, перемещаясь по ней, как в аксиальном, так и перпендикулярном к нему направлениях, совершая криволинейный характер движения.
Отнесем движущуюся частицу материала к осям координат x, z, приняв левую систему отсчета. Тогда дифференциальные уравнения движения частицы в проекциях на оси координат можно написать так (при условии, что N2 > 0):
Приняв теперь во внимание, что r = r0 = const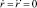 
, и подставив в уравнение значения и получим:
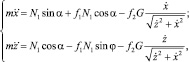(1)
где m – масса частицы, кг; 
– вторая производная от перемещения по оси x, м/с2; f1 – коэффициент трения частицы о элемент спиральной поверхности; α = cost – угол наклона винтовой линии рабочего органа к плоскости поперечного сечения спиральной поверхности, град; f2 – коэффициент трения частицы о поверхность кольца; 
– первая производная от перемещения по оси x, м/с; 
– первая производная от перемещения по оси z, м/с; 
– вторая производная от перемещения по оси z, м/с2.
После нескольких математических преобразований получим уравнение с одним неизвестным относительно координаты x:
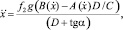(2)
где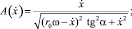 
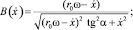
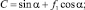
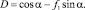
Полученные дифференциальные уравнения, описывают движения частицы материала по образующей спирально-винтовой поверхности рабочего органа.
Библиографическая ссылка
Артемьев В.Г., Исаев Ю.М., Семашкин Н.М., Гришин О.П. ПЕРЕМЕЩЕНИЕ ЧАСТИЦЫ ВИНТОВЫМ УСТРОЙСТВОМ ПО ПЛОСКОСТИ // Современные наукоемкие технологии. – 2013. – № 3. – С. 65-65;URL: https://top-technologies.ru/ru/article/view?id=31511 (дата обращения: 21.11.2024).