Проблема финишной обработки деталей с плоскими поверхностями из труднообрабатываемых материалов всегда является актуальной. Важным резервом повышения качества и производительности обработки таких деталей может служить широкое использование усовершенствованного технологического процесса торцового шлифования алмазными кругами с прерывистой рабочей поверхностью с подачей смазочно-охлаждающей жидкости непосредственно в зону резания [1].
Внедрение такого инструмента в промышленность предопределяет решение некоторых вопросов оптимизации процесса обработки.
Установить оптимальные условия ведения процесса, обеспечивающие, например, получение заданной шероховатости обработанной поверхности (Rа, мкм), расхода алмазов (q, мг/г), тангенциальную составляющую силы резания (Pz, H) при одновременном изменении различных факторов, например, поперечной подачи (Х1)-Sпоп=0,3...0,5 мм/ход, скорости перемещения детали X2-Vд=1,0...2,0 м/мин, глубины шлифования (Х3)-t=0,1...0,3 мм, скорости вращения алмазного круга (Х4)-Vкр=15...23 м/с позволяет применение метода центрального композиционного ротатабельного униформ планирования второго порядка [2].
В работе исследовалось шлифование пластин из стали 18ХН3А кругом А4К 150х32х40 АС6 100/80 - МО4-100, СОЖ - 1,5% содовый раствор.
В ходе реализации полнофакторного эксперимента 24 с дополнительными 8-ю «звездными» точками с плечом b=±2,0 и 7-ю «нулевыми» точками в центре плана получены уравнения регрессии [зависимости YRa = f(X1, X2, X3, X4), Yq = f(X1, X2, X3, X4), YPz = f(X1, X2, X3, X4)].
Интерпретация результатов исследования упрощается при анализе поверхности отклика (YRa, Yq, YPz ) в области оптимума графическим методом с помощью двухмерных сечений. Исходные уравнения регрессии в этом случае преобразуются в каноническую форму.
На рис.1 представлены двухмерные сечения поверхностей отклика: Ra=f(Vд, Vкр); q= f(Vд, Vкр); PZ= f(Vд, Vкр) в факторной плоскости Vд - Vкр при заданных глубине шлифования t=0.2 мм и поперечной подаче Sпоп = 0,3 мм/ход.
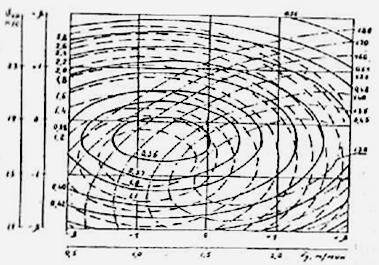
Рис.1. Двухмерные сечения поверхностей отклика
![]() контурная линия
равной шероховатости Ra, мкм
контурная линия
равной шероховатости Ra, мкм
![]() контурная линия
равной тангенциальной составляющей силы резания PZ, Н
контурная линия
равной тангенциальной составляющей силы резания PZ, Н
![]() контурная линия
равного удельного расхода алмазов q, мг/г
контурная линия
равного удельного расхода алмазов q, мг/г
в факторной плоскости скорости детали Vд - скорость круга Vкр при глубине шлифования t=0,2 мм.
Специальный алмазный прерывистый инструмент: АЧК 150х32х40 АС6 100/80-М04-100%, обрабатываемый материал 18ХН3А, СОЖ-1.5% содовый раствор.
В определенной производственной ситуации выбирается соответствующий критерий оптимизации при наложении некоторых ограничений на остальные выходные параметры.
Например, требуется получить шероховатость поверхности Ra=0,37 мкм при t=0,2мм. Это достигается сочетанием режимов шлифования Vд и Vкр, соответствующих координатам всех точек, принадлежащих контурной линии равного отклика Ra=0,37 мкм. Но, чтобы выбрать оптимальный вариант, необходимо учесть другие условия.
Так, при Vд=0,75 м/мин и Vкр=16 м/с обеспечивается PZ=160 Н, q=1,0 мг/г, а при Vд=1,5 м/мин, Vкр=20 м/с - PZ=145 Н, q=1,35 мг/г. Последнее сочетание режимов резания предпочтительнее, при этом сохраняется заданное значение Ra=0,37 мкм.
Таким образом, использование одного из методов математического планирования при исследовании процесса торцового шлифования специальным алмазным кругом с прерывистой рабочей поверхностью позволяет получить математические модели зависимости параметров шлифования от режимов резания. Последующая геометрическая интерпретация этих моделей и применение «наложенных сечений» дает возможность выбирать такое сочетание режимов резания, которое обеспечивает получение заданных (необходимых) показателей процесса.
СПИСОК ЛИТЕРАТУРЫ:
1. Патент РФ №209522, 6В24В 55/02, В24 Д 7/10. Абразивный инструмент для плоского шлифования / Свитковский Ф.Ю. и др. (Россия). Заявл. 4.03.96, опубл. 10.11.97, бюл. №31. - 3с.
2. Спиридонов А.А., Васильев Н.Г.. Планирование эксперимента.- Свердловск: 1975.
Библиографическая ссылка
Каракулова М.Л., Шитова Т.В. НЕКОТОРЫЕ ВОПРОСЫ ОПТИМИЗАЦИИ ПРОЦЕССА АЛМАЗНОГО ПРЕРЫВИСТОГО ШЛИФОВАНИЯ // Современные наукоемкие технологии. 2009. № 8. С. 115-116;URL: https://top-technologies.ru/ru/article/view?id=25668 (дата обращения: 13.03.2026).



