Анализ динамики распространения нововведений позволяет учитывать влияние научно-технического прогресса в классических экономических моделях. Рассмотрим этот подход на примере следующей модификации производственной функции Кобба-Дугласа (см. [1]):
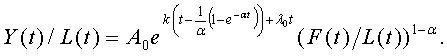
Здесь:
- Y(t) - объем произведенной промышленной продукции;
- L (t) - число занятых в производственной сфере;
- F(t) - основные производственные фонды;
- α - коэффициент, характеризующий нововведения с высокой скоростью распространения;
- λ0 - коэффициент, характеризующий нововведения со средней и низкой скоростями распространения;
- A0, k - постоянные положительные коэффициенты.
На основе данных о валовом внутреннем продукте, основных производственных фондах и числе зянятых в производственной сфере по Российской Федерации за период с января 1998г. по декабрь 2000г. методом наименьших квадратов нами произведена оценка неизвестных коэффициентов выбранной модели. Основная трудность с математической точки зрения в данном случае заключалась в том, что полученная для оценки неизвестных параметров система не только не является линейной, но и имеет бесконечное множество решений. Для определения набора значений параметров, минимизирующего сумму квадратов отклонений модельных данных от реальных, был произведен перебор с определенным шагом по параметру λ0. Качество полученной модели оценивалось с помощью коэффициента детерминации.
Получены следующие результаты при количестве наблюдений n = 14:
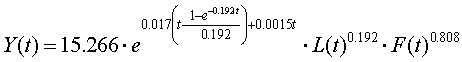 .
.
Коэффициент детерминации построенной модели равен 0.65227.
Небольшое значение коэффициента детерминации является, по-видимому, следствием того, что использованные при оценке неизвестных параметров модели данные соответствуют кризисному состоянию экономики. Непредсказуемое поведение экономических показателей в такой ситуации отрицательно сказывается на качестве модели. Попытка улучшить качество модели за счет увеличения количества наблюдений не привела к желаемому результату. Это вызвано, скорее всего, тем, что увеличение числа наблюдений ведет к увеличению временного интервала, а значит, мы уже не можем считать постоянным эффект от внедрения относительно медленно распространяющихся наблюдений.
СПИСОК ЛИТЕРАТУРЫ:
- Варшавский А. Е. Научно-технический прогресс в моделях экономического развития. - М.: Финансы и статистика, 1984.
Библиографическая ссылка
Копотева А.В. УЧЕТ ДИНАМИКИ РАСПРОСТРАНЕНИЯ НОВОВВЕДЕНИЙ В МАКРОМОДЕЛИ С НЕИДЕНТИФИЦИРОВАННЫМИ ФАКТОРАМИ ЭКОНОМИЧЕСКОГО РОСТА // Современные наукоемкие технологии. 2008. № 4. С. 167-168;URL: https://top-technologies.ru/ru/article/view?id=23808 (дата обращения: 25.12.2025).



