Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Рукавишников В.В. Белик А.В.

Статья в формате PDF

225 KB

В настоящей работе предлагается новый, более простой и доступный химикам подход, базирующийся на модели DENSON [2]. Новизна его состоит в том что, в конечном итоге, атомы в молекуле не имеют сферической симметрии, в сравнении с более ранним подходом [3].

Для получения пространственной формы молекулы требуется знание декартовых координат атомов ее составляющих. Такую информацию можно получить, например, в рамках вычислительного комплекса "Hyper Chemistry" [4] посредством оптимизации геометрии молекулы одним из доступных методов, вычисляя полную энергию системы методом РМ3. Далее каждому типу атомов Периодической системы Д.И.Менделееева приписывается собственный атомный радиус (r⁰), являющийся параметром модели. В частности, нами предлагается в качестве r⁰ для атома водорода принять величину в 0,3325 ангстрем. Соответственно для атома углерода - r⁰ (С) =0,6500 . Предполагается, что в результате атом-атомного взаимодействия в молекуле сферические оболочки атомов должны деформироваться. Величина деформации (∆r⁰) для атомов, находящихся на валентных расстояниях, вычисляется по формуле (1), где R_{i µ} евклидово расстояние между атомами i и μ ; n - главное квантовое число атома μ. Для невалентных взаимодействий такая поправка имеет вид (2). Очевидно, что если рассматриваемый атом имеет несколько соседних атомов, с которыми есть взаимодействие, то исходная сферическая оболочка будет деформироваться в разных направлениях и на разную величину. Предлагается простой механизм трансформации исходной атомной оболочки.

Δr_i = r_µ⁰ exp (R_{i µ})/ R_{i µ} ^n-1                                                (1)

Δr_i = - r⁰_μ exp (R_{μ j})/ R_{μ j} ⁶ - r⁰_μ exp (R_{μ j})/ R_{μ j} ¹²                      (2)

В начале поверхность каждого из атомов молекулы разбивается на N- точек, координаты которых запоминаются. Далее для каждой из точек поверхности атома рассматриваются все возможные взаимодействия и строятся вектора различного направления и значения согласно вычисленным ∆r. В итоге имеем для каждой точки несколько векторов для которых потом находится результирующий. Координаты конца результирующего вектора запоминаются и определяют местоположение новой точки поверхности атома с учетом всех взаимодействий.

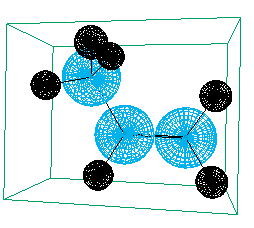
На рисунке видны результаты трансформации исходной атомной оболочки каждого из атомов молекулы на примере пропилена. На сколько новый молекулярный объем получил удовлетворительную оценку можно определить путем сравнения экспериментальных и вычисленных величин относительных плотностей веществ при 20^оС (d₄²⁰), как это и делалось ранее [2,3]. Отдельные результаты расчетов приведены в таблице.

    без учета атомных взаимодействий                                    с учетом атомных взаимодействий

Рисунок 1. Вид молекулы пропилена без учета атомных взаимодействийи с их учетом

Таблица 1. Экспериментальные d₄²⁰(эксп.) [5] и вычисленные d₄²⁰(расч.) относительные плотности некоторых углеводородов

Анализ полученных результатов показывает, что согласие теории и эксперимента удовлетворительное.

Разработанное программное обеспечение на базе предложенного алгоритма требует незначительных компьютерных ресурсов. В программе реализована полная визуализация процесса деформации атомных оболочек.

СПИСОК ЛИТЕРАТУРЫ

1. Бейдер Р. Атомы в молекулях: Квантовая теория.-М.:Мир, 2001.-532с.
2. Белик А.В. Компьютерное моделирование атомных радиусов для прогноза плотности органических веществ //Изв. вузов. Сер. Химия и хим. технология.1992. Т. 35, №4. С.51-55.
3. Белик А.В., Потемкин В.А. Новый подход к компьютерному моделированию атомных радиусов //ЖОХ. 1993. Т.63. Вып.6. С.1201-1203.
4. http: //www.hyper.com.
5. Свойства органических соединений. Справочник / Под ред. А. А. Потехина. Л.: Химия, 1984. 520 С.

Библиографическая ссылка