Закон движения объекта управления можно представить системой обыкновенных дифференциальных уравнений в векторной форме:
(1)
где 
- вектор-функция с элементами 
,х - вектор с компонентами 
принадлежащий пространству управления Rn, u- вектор с компонентами 
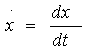производная вектора х по переменной t.
Общая форма математического описания закона движения объекта (1) задана в виде системы линейных дифференциальных уравнений с постоянными коэффициентами:
(2)
которая характеризует линеаризованное движение объекта управления в малой окрестности некоторой стационарной точки. Часто объект управления представляется системой линейных дифференциальных уравнений с переменными коэффициентами:
(3)
При оптимальном управлении движение объекта часто распространяется на большие области пространства состояний и не ограничено малой окрестностью некоторой стационарной точки. Поэтому математическое описание его нельзя линеаризовать, т. е. представить в форме (2). Приходится представлять объект управления в виде системы нелинейных дифференциальных уравнений.
Достаточно полно реальные объекты в энергетике, химии, металлургии, горном деле, обогащении и т. д. обычно можно описать в виде общей системы нелинейных дифференциальных уравнений
(4)
где А (х) - матрица-столбец с элементами
,..., 
; В(х)-матрица размером 
элементами 
, 
, 
; и - вектор с компонентами , и1 , и2,..., ит, причем 
(здесь Rm - замкнутое ограниченное множество). Уравнение (4) линейно относительно вектора и, и это обстоятельство значительно упростит в дальнейшем решение задач оптимального управления [2].
Математическое описание динамических режимов производственных циклов базируется на уравнениях материального и энергетического баланса или на уравнениях равновесия сил, моментов, напряжений, токов и т.д. Несоответствие поступления объекту энергии или вещества с их расходом и вызывает переходные режимы. Варьируя объемом емкостей и расходами вещества или энергии, можно влиять на динамические процессы в объектах. Нелинейность функции, входящих в математическое описание объекта, определяется несколькими факторами: геометрией машины или аппарата; нелинейностью того физического или химического закона, который положен в основу технологического процесса; зависимостью коэффициентов функций от параметров процесса; свойствами материалов, из которых изготовлена машина или аппарат.
Ооперативное управление сложными технологическими процессами предоставляет пользователю технологию, позволяющую провести полный цикл обработки всей геолого-геофизической и промысловой информации с целью построения геологической модели месторождения углеводородов. Технология построения геологической модели залежи углеводородов, включающая все этапы обработки и анализа, начиная с ввода данных и заканчивая выдачей итоговых документов, опирающаяся на единую базу данных и позволяющая реализовать алгоритмы обработки и комплексирования разнородной информации в рамках одной системы.
Нами рассматриваются каждый из этапов: определяются решаемые задачи, входные и выходные данные, описываются технология и методы решения поставленных задач.
Процесс построения модели месторождения начинается с геологического анализа, целью которого является выявление и взаимная увязка стратиграфических, фациальных, структурно-тектонических особенностей строения месторождения и поиск закономерностей в их распределении во времени и в пространстве. Стратиграфические исследования начинают с изучения (стратификации) единичных разрезов скважин, затем переходят к изучению и установлению закономерностей строения отложений на площади их развития и их генетической интерпретации, т.е. к фациальному районированию [3].
СПИСОК ЛИТЕРАТУРЫ
- Анисимов С.А., Дынькин В.И. и др. Основы управления технологическими процессами. - М.: Наука, 1966.-167 с.
- Максимов М.И., Рыбицкая Л.П. Математическая модель процессов разработки нефтяных месторождений. - М.: Недра, 1976.-264 с.
- Мамиконов А.Р., Пискунов А.Н. Модели и методы проектирования информационного обеспечения АСУ. - М.: Статистика, 1978.-221 с.
Библиографическая ссылка
Утепбергенов И.Т., Калиева К.А., Кенжебаева Ж.Е. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПЕРАТИВНОГО УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМ ПРОЦЕССОМ В НЕФТЯНОЙ ПРОМЫШЛЕННОСТИ // Современные наукоемкие технологии. – 2005. – № 7. – С. 93-94;URL: https://top-technologies.ru/ru/article/view?id=23428 (дата обращения: 21.11.2024).