I случай. Разгон производим с помощью мгновенной силы [1, 2, 3], когда интервал действия силы стремится к нулю, тогда получим мгновенную силу в виде ![]() , где δ(t) - δ-функция Дирака [1]. Величину I0 будем называть единичным импульсом силы. При воздействии на свободное тело импульса силы I0 тело приобретает равное ему количество движения (импульс тела) P = mV0. Запишем II закон Ньютона
, где δ(t) - δ-функция Дирака [1]. Величину I0 будем называть единичным импульсом силы. При воздействии на свободное тело импульса силы I0 тело приобретает равное ему количество движения (импульс тела) P = mV0. Запишем II закон Ньютона
![]() (1)
(1)
Применим к уравнению преобразование Лапласа [1]
![]() (2)
(2)
Для тела, которое в начальный момент покоилось, ![]() . Кроме того, будем полагать, что
. Кроме того, будем полагать, что ![]() , тогда (2) запишется в виде
, тогда (2) запишется в виде
![]() (3)
(3)
Выполняя обратное преобразование Лапласа, будем иметь
![]() ;
; ![]() (4)
(4)
где H(t) - единичная функция Хевисайда [4], причем ![]() .
.
Вычислим работу, совершенную мгновенной силой
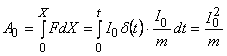 (5)
(5)
т.к. [1] 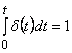
Так как ![]() , то работа разгона (затрата энергии)
, то работа разгона (затрата энергии) ![]() , где
, где ![]() - кинетическая энергия тела. То, что затраты энергии в два раза больше кинетической энергии можно объяснить эффектом «внезапной нагрузки» [2].
- кинетическая энергия тела. То, что затраты энергии в два раза больше кинетической энергии можно объяснить эффектом «внезапной нагрузки» [2].
Во всех курсах физики утверждается: для того, чтобы неподвижное свободное тело массы разогнать до скорости V0, необходимо затратить работу A, равную кинетической энергии тела [6]: ![]() , т.е. КПД процесса разгона тела
, т.е. КПД процесса разгона тела ![]() Однако известно, что если на тело подействовать внешней силой, то прежде чем оно придет в движение, произойдет деформация тела (упругая, пластичная, неупругая, вязкая и т.д. в зависимости от свойств тела), т.е. часть работы внешней силы будет затрачена на смещение частиц тела относительно друг друга. В дальнейшем ограничимся рассмотрением только упругих тел.
Однако известно, что если на тело подействовать внешней силой, то прежде чем оно придет в движение, произойдет деформация тела (упругая, пластичная, неупругая, вязкая и т.д. в зависимости от свойств тела), т.е. часть работы внешней силы будет затрачена на смещение частиц тела относительно друг друга. В дальнейшем ограничимся рассмотрением только упругих тел.
II случай. Разгон тела за счет удара бойка.
В теории абсолютно упругого удара [6] рассматривается случай, когда тело массы движется со скоростью V1 и сталкивается с точно таким же телом массы , но неподвижным. Результат получают из общего решения в таком виде: первое тело останавливается, а второе начинает движение со скоростью первого.
Рассмотрим задачу о прямом центральном ударе двух одинаковых упругих тел (двух стержней одинаковой длины ![]() ) первый из которых налетает со скоростью V0 на неподвижный второй стержень (рис.1). Запишем волновые уравнения для продольных смещений U(x,t) [7,8] для каждого из стержней и соответствующие краевые и начальные условия:
) первый из которых налетает со скоростью V0 на неподвижный второй стержень (рис.1). Запишем волновые уравнения для продольных смещений U(x,t) [7,8] для каждого из стержней и соответствующие краевые и начальные условия:
![]() , 0 < x < 1 (6)
, 0 < x < 1 (6)
![]() ,
, ![]()
Краевые условия:
![]()
![]()
![]()
![]() (7)
(7)
Начальные условия:
![]()
![]() (8)
(8)
![]()
![]()
Для одинаковых тел c1 = c2 = c - скорость распространения упругих волн (скорость звука), E1 =E2 = E = pc2 - модуль Юнга, ρ -плотность материала тел. Для решения задачи воспользуемся методом преобразования Лапласа [4,5] по переменной t. Решение задачи в изображениях имеет вид
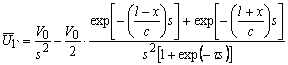 (9)
(9)
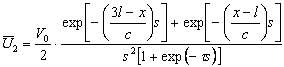 (10)
(10)
где ![]() - обозначено время прохождения упругой волны через оба стержня. Решения для скоростей тел в изображениях:
- обозначено время прохождения упругой волны через оба стержня. Решения для скоростей тел в изображениях:
![]() (11)
(11)
![]()
Решения для скоростей V представлены на графиках (рис. 2, 3). Из графиков видно, что торцы стержней (![]() ) движутся как одно целое с постоянной скоростью V = 0,5V0, а сами стрежни испытывают периодические деформации растяжения-сжатия. Наиболее сильные колебания испытывают торцы стержней x = 0 и
) движутся как одно целое с постоянной скоростью V = 0,5V0, а сами стрежни испытывают периодические деформации растяжения-сжатия. Наиболее сильные колебания испытывают торцы стержней x = 0 и ![]() , их скорости периодически меняются от 0 до V0.
, их скорости периодически меняются от 0 до V0.
Используя предельное соотношение для преобразования Лапласа [4, 5] для больших времен (t → ∞ ): ![]() при s → 0, из решений (11) следует, что в установившемся режиме все точки обеих стержней будут двигаться с одинаковой скоростью V1 = V2 = 0,5V0. Это означает, что половина начальной кинетической энергии K = mV0 / 2 теряется (энергия колебаний переходит во внутреннюю энергию). Чтобы разогнать неподвижный стержень до скорости V0, необходимо, чтобы первый стержень имел скорость 2V0, т.е. начальная кинетическая энергия должна быть в 4 раза больше: 4K0.Так как стержни одинаковые, то после удара кинетическая энергия распределится между стержнями поровну, второй стержень получит энергию 2K0, которая и обеспечит ему скорость V0.
при s → 0, из решений (11) следует, что в установившемся режиме все точки обеих стержней будут двигаться с одинаковой скоростью V1 = V2 = 0,5V0. Это означает, что половина начальной кинетической энергии K = mV0 / 2 теряется (энергия колебаний переходит во внутреннюю энергию). Чтобы разогнать неподвижный стержень до скорости V0, необходимо, чтобы первый стержень имел скорость 2V0, т.е. начальная кинетическая энергия должна быть в 4 раза больше: 4K0.Так как стержни одинаковые, то после удара кинетическая энергия распределится между стержнями поровну, второй стержень получит энергию 2K0, которая и обеспечит ему скорость V0.
В курсах физики [6] рассматривается абсолютно упругий удар двух тел. На самом же деле рассматривается удар двух «упругих материальных точек», а «упругая материальная точка» - это такой же нонсенс, как «жареный лед». Для указанной выше задачи для двух тел записываются законы сохранения импульса и энергии в следующем виде
![]() (12)
(12)
![]() (13)
(13)
где ![]() - начальный импульс первого тела,
- начальный импульс первого тела, ![]() - его импульс после удара,
- его импульс после удара, ![]() - импульс второго тела после удара. Решение получают в таком виде: V0=0, V1=V2. Этот результат противоречит результатам в рассмотренной нами задачи об упругом ударе двух стержней. В чем причина ошибки? Ошибка содержится в законе сохранения энергии (13). Если переписать закон сохранения импульса (который обычно записывают в виде
- импульс второго тела после удара. Решение получают в таком виде: V0=0, V1=V2. Этот результат противоречит результатам в рассмотренной нами задачи об упругом ударе двух стержней. В чем причина ошибки? Ошибка содержится в законе сохранения энергии (13). Если переписать закон сохранения импульса (который обычно записывают в виде ![]() ) с помощью теоремы косинусов, то будем иметь
) с помощью теоремы косинусов, то будем иметь
![]() (14)
(14)
и из него закон сохранения энергии в виде
![]() (15)
(15)
Последний член соответствует энергии упругих колебаний. Решением системы (14) (15) являются ![]() , т.е. оба тела движутся с одинаковой скоростью
, т.е. оба тела движутся с одинаковой скоростью ![]() и при этом совершают упругие колебания относительно центра масс системы. Через некоторое время за счет дисперсии и внутреннего трения энергия упругих колебаний переходит во внутреннюю энергию (тела нагреваются).
и при этом совершают упругие колебания относительно центра масс системы. Через некоторое время за счет дисперсии и внутреннего трения энергия упругих колебаний переходит во внутреннюю энергию (тела нагреваются).
Таким образом, проведенные исследования показали, что для разгона первоначального неподвижного тела путем ударного нагружения требуется сообщить ему энергию, равную двум кинетическим энергиям. Одна кинетическая энергия расходуется на энергию упругих колебаний, которая переходит во внутреннюю энергию тела. Таким образом КПД процесса разгона ![]() .
.
СПИСОК ЛИТЕРАТУРЫ
- Арфкен Г. Математические методы в физике. - М.: Атомиздат, 1970.
- Иванов Е.М. Дополнительные главы классической механики. - Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических сил //Успехи современного естествознания. - 2004. - № 9. - С.10.
- Дёч Г. Руководство к практическому преобразования Лапласа и Z-преобразования. - М.: Наука, 1971.
- Бейтмен Г., Эрдей иА. Таблицы интегральных преобразований. - Том I. - М.: Наука, 1969.
- Сивухин Д.В. Общий курс физики. Том I. Механика.-М.: Наука, 1989.
- Тихонов А.Н., Самарский А.А. Уравнения математической физики. - М.: Наука, 1966.
- Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математике.
Библиографическая ссылка
Иванов Е.М. РАБОТА РАЗГОНА НЕПОДВИЖНОГО ТЕЛА // Современные наукоемкие технологии. – 2005. – № 6. – С. 9-11;URL: https://top-technologies.ru/ru/article/view?id=23063 (дата обращения: 26.04.2024).



