an+bn=cn (1)
справедливо только при n=1;2 (n ≥1 , кроме трансцендентных значений).
Доказательство.
Для функции 
, следующей из (1), установлено 
, или (2) 
, где 
. (3)
Разделим обе части (3) на ab, что не повлияет на каждый член в отношении его рациональности,
, (4)
где 
. При целых (рациональных) a,b число u рационально.
Приведем члены в (4) к единой форме
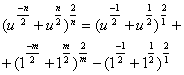(5)
Обозначив 
, получим (6)
; 
;
;
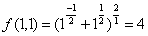; . (7)
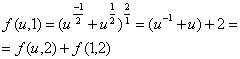
Из (5) с учетом (6), (7) имеем 
, или (8)
. (9)
При рациональном u значения 
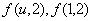рациональны, поэтому числа n,m в отношении рациональности имеют общий характер, в частных случаях они равны между собой.
Так, из (8) следует, что при m=1 
, то есть n=m=1,c = a+b , а на основании (9) при m=2 
,n=m=2 ,
. В первом случае числа a,b,c могут быть любыми, в том числе рациональными (целыми), а во втором - целыми (рациональными), если они обладают признаками чисел Пифагора:
, где U,V - целые (взаимно простые, одно из них четное, второе нечетное) или рациональные числа. При u=1 
,n=m ,
.
В остальном положим, что 
рационально (соответствует рациональному c), тогда рациональным обязано быть 
(
, так как 
).
Число D иррационально при рациональном m (кроме m=1;2), при иррациональном m оно трансцендентно (число Гильберта) и только при трансцендентном m может быть рациональным (значение 
при рациональном D трансцендентно, кроме D=2;4, когда m=1;2).
Следовательно, наряду с n=1;2, целыми (рациональными) a,b,c в (1) могут быть только при трансцендентных n. Также справедливо утверждение, что хотя бы одно из них выпадает из этого ряда, если n целое (рациональное) (n≠1;2 ) или иррациональное.
Таким образом, теорема доказана.
Работа представлена на научную конференцию с международным участием «Фундаментальные исследования», Доминиканская республика, 5-16 апреля 2006г. Поступила в редакцию 14.03.2006г
Библиографическая ссылка
Соколов Г.М. ОБЩАЯ ПОСЛЕДНЯЯ ТЕОРЕМА П. ФЕРМА // Современные наукоемкие технологии. – 2006. – № 4. – С. 82-83;URL: https://top-technologies.ru/ru/article/view?id=22653 (дата обращения: 21.11.2024).