Повышение эффективности производства и качества изделий легкой промышленности необходимо обеспечивать на этапе проектирования продукции за счет применения научных методов исследования и математического моделирования технологических процессов. Вопросам повышения качества изделий из трикотажных полотен на основе результатов экспериментальных исследований уделяется большое внимание. Так, в работах [1–3] рассмотрены способы решения исследовательских задач для обеспечения качества трикотажных изделий. При конструировании изделий из трикотажных материалов крайне важно учесть величину условно-остаточной деформации и усадки. В статье [4] приведены результаты экспериментальных исследований и разработана на их основе методика расчета конструктивных параметров женских изделий с учетом остаточных деформаций трикотажа. Учет усадки возможен различными способами. Один из них – предусмотреть необходимую прибавку при расчете базовой конструкции изделия. Для того, чтобы величина прибавки соответствовала величине усадки полотна, следует разработать математическую модель, позволяющую установить зависимость усадки полотен от их свойств структурных характеристик. Данные исследования также будут способствовать развитию ресурсосберегающих технологий, что является весьма актуальной задачей, отраженной в работах [5–6].
Цель работы – повышение точности процесса конструирования изделий из трикотажных полотен за счет учета и прогнозирования величины их усадки на основе данных математического моделирования
Материалы и методы исследования
Для исследования влияния структурных характеристик трикотажных полотен на величину усадки были взяты девять образцов трикотажных полиакрилонитрильных (ПАН) полотен.
Испытания проводились согласно ГОСТ 30157.0-95 и ГОСТ 30157.1-95, в соответствии с которыми был выбран режим испытания С11П8О7В4Г7.
Режимы испытания представлены в таблице.
Режимы испытания
|
Параметры испытания |
Модуль ванны |
Температура воды, °С |
Масса моющего средства, г/дм3 |
Продолжительность, мин: – без механических воздействий |
|
1 |
2 |
3 |
4 |
5 |
|
С11 – режим ручной стирки |
1:30 |
40 ± 3 |
3 ± 0,5 |
10 ± 5 |
|
П8 – ванна для полоскания |
1:30 |
21 ± 3 |
Количество циклов 3 |
3 ± 0,1 |
|
О7 – режим обезвоживания |
– |
– |
– |
60 ± 6 |
|
В4 – режим высушивания |
– |
Комнатная температура |
– |
Не менее 720 мин |
|
Г7 – режим глажения и прессования |
– |
115 ± 15 |
– |
20 ± 1 |
Программа проведения исследования включает следующие этапы:
– подготовка образцов;
– проведение исследования;
– обработка данных и определение усадки;
– определение структурных характеристик трикотажных полотен;
– получение математической модели зависимости усадки от характеристик трикотажных материалов.
Проведение эксперимента осуществлялось в соответствии с выбранными режимами испытаний, представленных в таблице. В результате для различных образцов была определена: усадка линейная по длине Уд и ширине Уш, поверхностная Уs и объемная Уv усадка.
Определение структурных характеристик трикотажных полотен проводилось в соответствии с методикой, изложенной в [7]. Для обеспечения автоматического расчета структурных характеристик трикотажных полотен была разработана информационная технология их определения с использованием электронных таблиц Microsoft Office Excel [8]. На рис. 1 представлены фрагменты определения структурных характеристик трикотажных полотен в программе Microsoft Office Excel
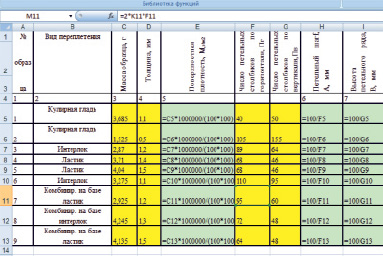
а
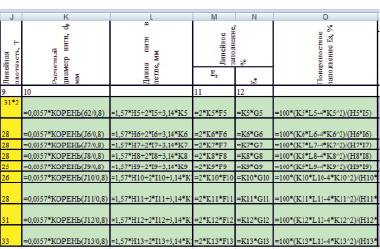
б
Рис. 1. Фрагменты электронной таблицы определения структурных характеристик трикотажных полотен
После определения структурных характеристик экспериментальным путем и в автоматизированном режиме в разработанной программе, а также значений усадки, полученных в ходе проведения эксперимента, было проведено математическое моделирование.
Для построения математической модели зависимости усадки от структурных характеристик трикотажных полотен в работе был использован многомерный регрессионный анализ [9]. В матричной форме многомерная регрессионная модель имеет вид
Y = Х×В + ε, (1)
где Х – матрица входных параметров; Y – вектор-столбец выходных параметров; B – вектор-столбец неизвестных коэффициентов; ε – вектор-столбец случайных «ошибок».
Неизвестные коэффициенты находятся методом наименьших квадратов при условии минимизации скалярной суммы квадратов по компонентам вектора В: Q = (Y – X×B)T(Y – X×B) → min. Решая это уравнение, получаем выражение для нахождения неизвестных коэффициентов в матричном виде:
В = (XT X)-1 XT Y. (2)
В качестве факторов были выбраны: Х1 – поверхностная плотность материала; Х2 – линейное заполнение пряжи; Х3 – линейное заполнение по горизонтали; Х4 – линейное заполнение по вертикали; Х5 – поверхностное заполнение. В качестве параметров оптимизации: У1 – усадка по длине; У2 – усадка по ширине; У3 – поверхностная усадка.
Построение многомерной регрессионной математической модели проводилось в программе Mathcad в соответствии со следующими этапами:
1. Ввод исходных данных.
2. Определение математических ожиданий и средних квадратических отклонений.
3. Нормирование параметров.
4. Построение математических моделей зависимости усадки по длине, усадки по ширине и поверхностной усадки от структурных характеристик трикотажных полотен.
5. Проверка адекватности математических моделей.
Фрагмент программы построения многомерных математических моделей в системе Mathcad на этапе ввода данных и начальной математической обработки представлен на рис. 2.
Фрагмент программы построения многомерных математических моделей в системе Mathcad на этапе нормирования показателей и получения коэффициентов регрессии представлен на рис. 3.
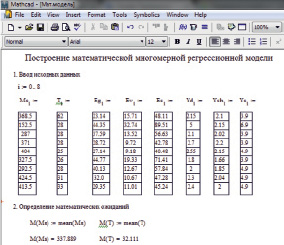
Рис. 2. Фрагмент программы на этапе ввода данных и определения статистических характеристик

Рис. 3. Фрагмент программы построения математической модели
Результаты исследования и их обсуждение
Таким образом, в работе для определения структурных характеристик трикотажных полотен с использованием программы Microsoft Office Excel была сформирована электронная таблица, представленная
на рис. 4.
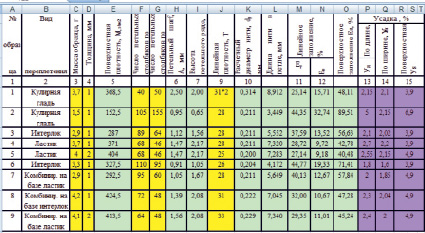
Рис. 4. Электронная таблица расчета структурных характеристик трикотажных полотен
В колонки, выделенные желтым цветом, заносятся показатели полотен, определенные экспериментальным путем.
В колонках, выделенных зеленым цветом, происходит автоматический расчет характеристик трикотажных полотен по заранее внесенным формулам в соответствующие ячейки электронной таблицы.
В результате проведения компьютерного моделирования в программе Mathcad были получены следующие математические модели:
У1 = 1,653 – 1,091Х1 – 0,356Х2 – 0,752Х3; (3)
У2 = 2,111 – 0,031Х1+0,037Х2 – 0,035Х4; (4)
У3 = 4,886 – 0,218Х1 – 0,138Х2+0,3Х5. (5)
В работе предложен автоматизированный способ расчета прогнозируемой величины усадки с использованием разработанной электронной таблицы, представленной на рис. 4. Так, в соответствующие ячейки, выделенные сиреневым цветом, занесены математические модели согласно формулам (3–5). При изменении характеристик трикотажных полотен происходит определение усадки автоматически.
Выводы
Анализ математических моделей показал:
– в математической модели (3), характеризующей зависимость усадки по длине от характеристик трикотажа, наиболее значимым является коэффициент при факторе Х3 – линейное заполнение по горизонтали. При этом при увеличении линейного заполнения по горизонтали усадка уменьшается, что соответствует изложенным в литературе сведениям о том, что увеличение числа петель на 100 мм снижает усадку, поскольку линейное заполнение напрямую зависит от числа петельных столбиков по горизонтали;
– в математической модели (4), характеризующей зависимость усадки по ширине от характеристик трикотажа наиболее значимым является коэффициент при факторе Х4 – линейная плотность пряжи, при этом при увеличении линейной плотности усадка по ширине увеличивается, что также соответствует известному факту: при увеличении толщины нитей размеры полотна увеличиваются в направлении, перпендикулярном его поверхности;
– в математической модели (5), характеризующей зависимость поверхностной усадки от характеристик трикотажа, наиболее значимым является коэффициент при факторе Х5 – поверхностное заполнение, при этом при увеличении поверхностного заполнения, поверхностная усадка увеличивается, что также согласуется с известными сведениями: с увеличением длины петли изменение размеров по длине возрастает, поскольку величина поверхностного заполнения находится в прямой зависимости от длины петли.
Полученные математические модели позволяют установить зависимость величины усадки от комплекса характеристик: поверхностной плотности, линейной плотности пряжи, величин линейного и поверхностного заполнения, которые в свою очередь учитывают такие характеристики, как число петельных столбиков и петельных рядов, диаметр нити, длина нити в петле. Данные математические модели позволят прогнозировать величину возможной усадки в зависимости от структурных характеристик трикотажных полотен, с учетом которой при конструировании уточняются необходимые прибавки.



