Область применения программного обеспечения в современном информационно развитом мире чрезвычайно широка и включает приложения, требующие высокого уровня надежности и обеспечения устойчивости к ошибкам. Программное обеспечение является неотъемлемой частью промышленных систем управления и информационно-управляющих систем критичных областей, где отказ этих систем может повлечь за собой критические последствия и имеет негативное влияние на жизнь и здоровье людей или финансовое состояние как предприятия, так и целого региона. К таким критическим областям относятся атомная энергетика, космическое и авиастроение, химическое производство, металлургия, банковский сектор.
Проблема надежности программ стала актуальной практически с появлением программного обеспечения и остается таковой по сей день. Естественно, что с развитием информационных технологий, созданием новых средств разработки и анализа программного обеспечения развивались и совершенствовались методы и механизмы, направленные на повышение надежности программ. К числу положительно зарекомендовавших себя методов обеспечения отказоустойчивости программного обеспечения можно отнести такие, как обработка исключений, контрольные точки и рестарт, парные процессы [5].
На сегодняшний день создан ряд различных подходов, гарантирующих отказоустойчивость программного обеспечения к аппаратным и программным ошибкам, основанных на программной избыточности. Среди них можно выделить мультиверсионное программирование и программное обеспечение с блоком восстановления [8, 9].
Оба этих подхода предполагают генерацию набора функционально эквивалентных программных компонент, реализующих различные методы и алгоритмы решения задачи. В мультиверсионном программном обеспечении эти компоненты выполняются параллельно и одновременно, полученные результаты оцениваются, и один из них принимается как верный [6, 10]. В программном обеспечении с блоком восстановления сначала выполняется первичный программный компонент, результат оценивается приемочным тестом, и в том случае, если он оказался ошибочным, вызывается альтернативный компонент [1, 10]. Альтернативных программных компонентов (или альтернатив) может быть несколько. На рис. 1 представлен блок восстановления в общем виде.
Приемочный тест пройден при проверке результатов первичного компонента;
иначе альтернативы 1;
иначе альтернативы 2;
…
иначе альтернативы n;
в противном случае – ошибка.
Рис. 1. Блок восстановления
Программное обеспечение с блоком восстановления отличается приемочными тестами, создаваемыми под конкретную задачу, которую и решают альтернативы. Последовательное выполнение альтернатив в случае отказа предыдущих требует меньше вычислительных ресурсов, поскольку в текущий момент времени выполняется только одна альтернатива, а не множество мультиверсий. В данной статье предлагается подход к моделированию и анализу свойств на основе сетей Петри программного обеспечения с блоком восстановления.
Цель представления системы в виде сети Петри и последующего анализа этой сети состоит в получении важной информации о структуре и динамическом поведении моделируемой системы [3]. Сети Петри предназначены для моделирования систем, которые состоят из множества взаимодействующих друг с другом компонент [3]. Это обосновывает и позволяет с успехом применить сети Петри для моделирования и анализа программного обеспечения с блоком восстановления.
Моделирование программ с блоком восстановления с помощью сетей Петри
Рассмотрим общий подход к анализу программ с блоком восстановления с помощью сетей Петри на примере блока восстановления с двумя программными компонентами – первичным и альтернативным. Данная модель может быть легко развита для любого произвольного количества альтернатив. Предложенная сеть Петри описывает переходы между состояниями, в которых может находиться программа, которые в конечном итоге приводят к отказу. Каждая позиция сети Петри соответствует какому-либо событию, а его наступление отражается посредством маркера в этой позиции. В частности, маркер в позиции P указывает на то, что выполняется первичный программный компонент.
Определим обозначения, которые будут использоваться при моделировании программы с блоком восстановления с помощью сети Петри. Первичному компоненту будет соответствовать обозначение P, альтернативному – S, а приемочному тесту – T. Появление ошибки в программных компонентах или тесте будем обозначать в виде подчеркивания соответствующего компонента.
При выполнении программы некоторые события будут рассматриваться с учетом событий, произошедших ранее. Такие события будут обозначаться несколькими символами, при этом предшествующие события будут представлены в виде нижнего индекса. Например, TP указывает на то, что выполняется тест результатов первичного программного компонента, при этом в последнем произошла ошибка.
Существует несколько траекторий движения маркера по сети Петри, в результате которых он окажется в позиции «Отказ» (рис. 2). Первая последовательность, P PT TP Отказ, может выполниться ввиду взаимосвязанных ошибок между первичным программным компонентом и приемочным тестом.
Вторая последовательность, P PS TPS SP TSP Отказ, может выполниться ввиду взаимосвязанных ошибок в первичном и альтернативном программном компонентах. В этом случае приемочный тест отвергнет результаты обоих программных компонентов, что приведет к отказу.
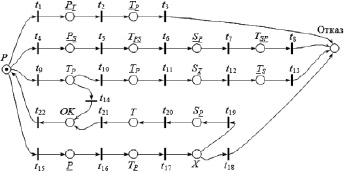
Рис. 2. Модель программы с блоком восстановления с двумя альтернативами
Третья последовательность, P TP TP ST TS Отказ, обусловлена ошибкой в приемочном тесте и описывает случай, когда приемочный тест отвергает любые результаты первичного и альтернативного программных компонентов.
Четвертая последовательность, P P TP X, выполняется в том случае, если в первичном программном компоненте произошла ошибка. Успешное выполнение блока восстановления зависит от того, сможет ли приемочный тест распознать ошибку. Эта ситуация моделируется посредством позиции X и переходов t18 и t19. Если приемочный тест распознает ошибку, то маркер перейдет в позицию SP, будет вызван альтернативный программный компонент, и работа блока восстановления завершится успешно (позиция OK). Можно отметить, что при таком развитии событий отказа альтернативного компонента не происходит, поскольку эта ситуация моделируется выполнением второй последовательности. Если же приемочный тест не распознает ошибку, возникшую в первичном программном компоненте, то маркер произойдет отказ (позиция Отказ).
Предложенная модель программы с блоком восстановления в виде сети Петри подробно описывает выполнение программы. Однако в некоторых случаях нет необходимости в детальном описании, а напротив, требуется упрощенная модель. Это особенно актуально, если сама модель выступает в дальнейшем как один из элементов более сложной модели.
Представленная на рис. 2 модель может быть упрощена посредством объединения переходов различных последовательностей. Полученная упрощенная модель представлена на рис. 3.
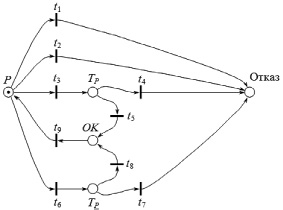
Рис. 3. Упрощенная модель программы с блоком восстановления с двумя альтернативами
Анализ безотказности программы с блоком восстановления
Предложенная модель программного обеспечения с блоком восстановления на основе сети Петри позволяет выполнить анализ его различных свойств. В частности, был проведен анализ безотказности работы программного обеспечения с блоком восстановления в зависимости от интенсивности отказов его отдельных компонентов. Проведенный анализ обусловлен тем, что применение блока восстановления направлено именно на обеспечение высокой надежности программ.
При анализе рассматривалась программа с двумя программными компонентами: первичным и альтернативным. Модель программы соответствует модели, приведенной на рис. 3. Полагалось, что интенсивность отказов компонентов имеет экспоненциальный закон распределения [2, 7]. В табл. 1–6 приведены значения безотказности анализируемой программы R при различных значениях интенсивности отказов компонент: λP – интенсивность отказов первичного компонента; λT – интенсивность отказов приемочного теста; λS – интенсивность отказов альтернативного компонента притом, что первичный компонент отказал; t – моменты времени, измеряемые в квантах.
Отметим, что табл. 5 и 6 соответствуют случаю, когда произошла ошибка как в первичном, так и альтернативном программных компонентах.
На основании результатов анализа можно судить о чувствительности безотказности программного обеспечения к ошибкам отдельных компонент. Так интенсивность отказов первичного компонента вносит наибольший вклад в значение безотказности программы с блоком восстановления (табл. 2). Высокая интенсивность отказов первичного программного компонента уменьшает безотказность всей программы в наибольшей степени, напротив, его низкая частота отказов приводит к наибольшей безотказности программы с блоком восстановления.
Таблица 1
Значения безотказности программы при λP = 0,01
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R |
1 |
0,9998 |
0,9996 |
0,9994 |
0,9992 |
0,999 |
0,9988 |
0,9986 |
0,9984 |
0,9982 |
0,998 |
Таблица 2
Значения безотказности программы при λP = 0,0001
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R |
1 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9997 |
0,9997 |
Таблица 3
Значения безотказности программы при λT = 0,001
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R |
1 |
0,9999 |
0,9998 |
0,9998 |
0,9997 |
0,9996 |
0,9995 |
0,9995 |
0,9994 |
0,9993 |
0,9992 |
Таблица 4
Значения безотказности программы при λT = 0,00001
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R |
1 |
0,9999 |
0,9999 |
0,9998 |
0,9998 |
0,9998 |
0,9997 |
0,9997 |
0,9997 |
0,9996 |
0,9996 |
Таблица 5
Значения безотказности программы при λS = 0,001
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R |
1 |
0,9999 |
0,9998 |
0,9997 |
0,9996 |
0,9994 |
0,9993 |
0,9992 |
0,999 |
0,9989 |
0,9988 |
Таблица 6
Значения безотказности программы при λS = 0,00001
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R |
1 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9998 |
0,9998 |
0,9998 |
0,9997 |
0,9997 |
0,9997 |
Заключение
В работе рассмотрена одна из программных архитектур – программное обеспечение с блоком восстановления – отличающаяся устойчивостью к ошибкам отдельных программных компонент. Для моделирования и анализа данного программного обеспечения предлагается применять сети Петри. В работе показано, каким образом программа с блоком восстановления, включающая два альтернативных программных компонента, может быть смоделирована посредством сетей Петри. Подробно описанный подход позволяет создать модель программы с блоком восстановления с любым числом альтернативных программных компонент. Кроме этого, показано, как детальная модель может быть преобразована в упрощенную модель, представленную также в виде сети Петри.
В статье приведены результаты анализа безотказности программы с блоком восстановления. На основе проведенного анализа выявлено, что наиболее критичной для общей надежности программы является интенсивность отказов первичного программного компонента. Показан вклад интенсивности отказов различных компонентов в изменение значений безотказности программы с блоком восстановления.
Предложенный подход может быть использован при моделировании не только программ с блоком восстановления, но и для моделирования и анализа других программных архитектур с избыточностью, например, мультиверсионного программного обеспечения или программного обеспечения схемы блока восстановления с согласованием [4], что может стать предметом дальнейших исследований.



