Износ пар трения в подшипниковых узлах нарушает их взаимодействие, может вызывать значительные дополнительные нагрузки, удары в сопряжениях и вибрации, а также стать причиной задиров и заклинивания с последующим разрушением как самого подшипникового узла, так и оборудования, в котором он установлен, что может привести к аварийной ситуации. Наибольший износ подшипников скольжения вызывает работа в режиме граничного трения [6].
Известно, что режим трения в гидродинамических опорах скольжения определяется коэффициентом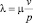 
, зависящим от вязкости смазывающей жидкости μ, скорости скольжения v и удельной нагрузки p [1]. Представление о переходе опоры из одного режима трения в другой даёт диаграмма Герси – Штрибека (рис. 1), представляющая собой зависимость коэффициента трения f от λ.
При разгоне вала до номинальной скорости вращения, устойчивый слой смазочного материала между поверхностями трения формируется не сразу, и подшипник последовательно проходит стадию смятия поверхностных микронеровностей втулки и вала, тангенциального смещения пар трения, граничного трения, смешанного трения и, наконец, переходит в режим жидкостного трения. Жидкостное трение – наиболее приемлемый режим, в котором поверхности пар трения разделены непрерывной плёнкой смазочного материала, толщина которой значительно превышает суммы средних высот шероховатостей пар трения. Изнашивание практически отсутствует. При уменьшении параметра λ толщина плёнки уменьшается и появляются контактные взаимодействия микронеровностей, наступает режим смешанного трения, при этом часть нагрузки воспринимается микронеровностями и возрастает изнашивание. При дальнейшем уменьшении λ значительно возрастает число контактов микронеровностей, а толщина плёнки ещё более уменьшается, до мономолекулярного слоя, который устраняет адгезионное взаимодействие пар трения, а нагрузка почти полностью воспринимается выступами микронеровностей. Возрастает также коэффициент трения. Перейти в режим смешанного и граничного трения подшипник может и при резком возрастании нагрузки. В таком случае локальная температура в зоне контакта двух поверхностей трения может превысить температуру плавления покрытия (например, баббита), что приводит к «свариванию» поверхностей друг с другом и, как следствие, аварии.
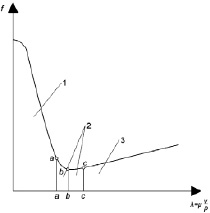
Рис. 1. Диаграмма Герси – Штрибека: 1 – граничное трение; 2 – смешанное трение; 3 – жидкостное трение
Чтобы предотвратить возможность выхода из строя из-за локального плавления покрытия и заклинивания подшипника, необходимо поддерживать режим жидкостного трения в опоре. Например, использование комбинированного режима работы: при таком изменении режима трения, что на диаграмме Герси – Штрибека точка смещается влево от линии b-b, происходит переход от гидродинамического способа поддержания разделительного слоя смазочного материала к гидростатическому. Определение перехода из режима смешанного трения в режим граничного трения измерением нагрузки и скорости скольжения пар трения невозможно для различных подшипников, без предварительных расчётов. Как видно из диаграммы, при уменьшении λ в режиме смешанного трения, а также переходе в режим граничного трения происходит резкое возрастание коэффициента трения. Следовательно, изменение режима трения со смешанного на граничное можно определить по изменению коэффициента трения.
Цель данной работы – разработка методики экспериментального определения режима трения в опоре скольжения.
Рассмотрим опору скольжения (рис. 2). Пусть вал под действием крутящего момента вращается с угловой скоростью ω относительно втулки, вес G которого вместе с силой нагружения P задаёт нагрузку на подшипник, перпендикулярную оси вращения. Момент силы трения вала [3]:
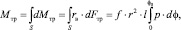(1)
где dFтр = f•dN – сила трения на элементарной площадке dS поверхности контакта; dN = p•dS – нормальное давление на элементе dS = r•dΦ•l; p – удельное давление; r – радиус вала.
Если предположить, что удельное давление распределяется по поверхности контакта равномерно p = const, а центральный угол Φ0 = π, а также, что нагрузка на вал P = 2•p•r•l, после интегрирования получим [7]:
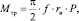(2)
тогда коэффициент трения будет равен
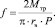(3)
В случае, если вращение вала производит двигатель постоянного тока с независимым возбуждением (ДПТ), то его механическая характеристика представляет собой прямую, которая описывается уравнением
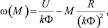(4)
где U – напряжение на якоре; R – полное сопротивление цепи якоря; k – конструктивный коэффициент двигателя; Ф – магнитный поток; M – момент двигателя M = kФI [4].
Так как упругость элементов в системе незначительна, считаем систему абсолютно жёсткой. В таком случае уравнение движения примет вид
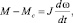(5)
где M – момент двигателя M; Mс – приведённый момент нагрузки; J – общий момент инерции двигателя и исполнительного механизма; ω – угловая скорость вращения вала двигателя [4].
Момент сопротивления на валу складывается из моментов трения двигателя Mтр.д, моментов трения редуктора Mтр.р, а также момента трения испытуемой опоры скольжения Mтр. В таком случае момент трения опоры скольжения можно найти из следующего выражения:
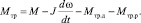(6)
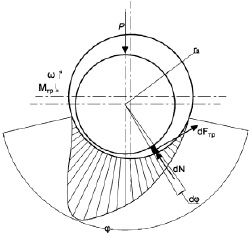
Рис. 2. Расчётная схема опоры скольжения
Исходя из выражений (3) и (6), а так же учитывая связь электромагнитного момента двигателя с током якоря, получим зависимость для нахождения коэффициента трения:
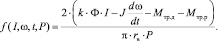(7)
Так как второй член в выражении (4)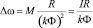 
показывает изменение скорости в зависимости от тока, а 
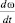показывает угловое ускорение вала двигателя, то уравнение (7) примет следующий вид:
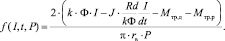(8)
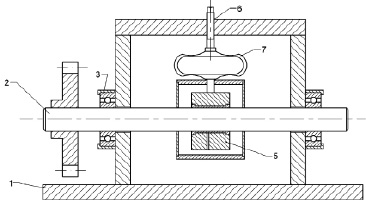
Рис. 3. Схема установки
Выражение позволяет оценить коэффициент трения в зависимости от потребляемого ДПТ тока и нагрузки, создаваемой на валу.
Как было отмечено, метод измерения коэффициента трения основан на измерении тока якоря I во времени при заданном значении нагрузки Р.
Для измерения разработан аппарат, способный производить измерение силы трения при любых условиях скольжения. Схема установки приведена на рис. 3.
Основные узлы смонтированы на раме 1. Испытываемый 2 вал вращается в двух шарикоподшипниках 3, установленных на раме 1. Двигатель постоянного тока (ДПТ), посредством ремённой передачи, приводит во вращение вал 2. В установке применяются гидродинамические подшипники скольжения с баббитовой заливкой 5. Подшипник окружён корпусом, предотвращающим выброс смазочной жидкости. Нагрузка к подшипнику прикладывается посредством домкрата 6. Измерение нагрузки производится с помощью динамометра 7.
Частота вращения вала задаётся компьютером, далее управляющие сигналы поступают на микроконтроллер, который управляет работой ДПТ. Измерение угловой скорости, момента сопротивления вращению вала, а также динамического момента производится измерением тока якоря датчиком холла с определённой частотой опроса. Сигнал с датчиков поступает на микроконтроллер и затем – на компьютер.
В заключение следует отметить, что кроме возможности определения режима трения предложенная методика позволяет определять коэффициент трения в опорах скольжения.