Рассматривается задача упаковки прямоугольников в квадрант (2DArea Packing Problem, 2DAP)) [9]: дано n прямоугольных предметов с размерами wi×hi, i = 1, 2, ..., n, требуется найти упаковку в положительном квадранте с минимальной площадью окаймляющего прямоугольника. При этом повороты запрещены, стороны прямоугольников параллельны осям координат. Формальная запись задачи: n – количество прямоугольников; wi, hi – длина и ширина i-го прямоугольника, i = 1, 2, ...; W, H – длина и ширина окаймляющего прямоугольника; W×H > min. Цель работы – синтез и анализ детерминированного параллельного алгоритма двумерной упаковки. Алгоритм строится на основе устойчивой параллельной сортировки с единичной временной сложностью [5] и видоизменения формул Виета восстановления коэффициентов полинома по его комплексным корням [2, 3], используемого для генерации всех сочетаний прямоугольников из заданного конечного множества.
Видоизменение формул Виета для параллельной генерации всех сочетаний прямоугольников
Коэффициенты полинома
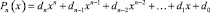
выражаются через его корни над полем комплексных чисел в виде [2, 3]:
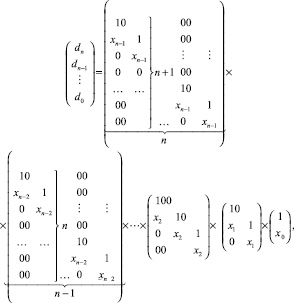 (1)
(1)
где xi – i-й корень полинома, i = 0, 1, ..., n – 1, предполагается, что dn = 1. С другой стороны, по формулам Виета [1], –
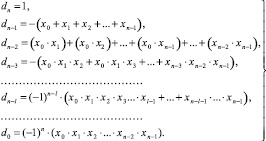 (2)
(2)
В (2), если не учитывать знак перед скобками, представлены все сочетания корней. Чтобы их выделить, требуется заменить знак умножения на знак «⊕», который понимается как перечисление элементов сочетания (без выполнения каких бы то ни было операций), знак суммы – на любой знак, обозначающий задание порядка сочетаний, в таком качестве ниже выбран знак «∨». Прямоугольники можно интерпретировать как взаимно однозначно сопоставленные комплексным корням полинома xj + Iyj в виде xj ⊕ yj, где xj – длина основания, yj – высота j-го прямоугольника, j = 0, 1, ..., n – 1. В данной трактовке (2) означает представление всех сочетаний из n прямоугольников, положение которых в декартовых координатах задано и не меняется. Поскольку (1) алгоритмически эквивалентно (2), то описанное преобразование (1) генерирует все сочетания прямоугольников из n по m в виде
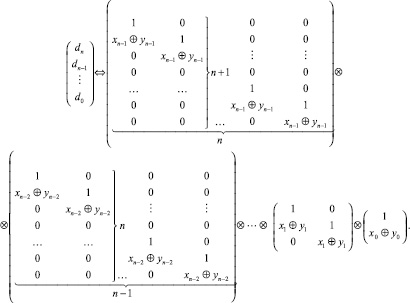 (3)
(3)
В силу совпадения левых частей (1), (2) результатом выполнения (3) окажется теоретико-множественный аналог соотношения (2), который можно представить в виде
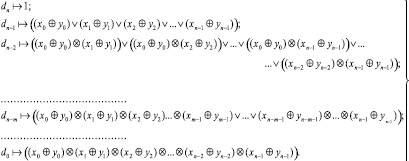 (4)
(4)
Соотношение (3) параллельно по строкам за n шагов генерирует все сочетания вида (4), которые не зависят от порядка прямоугольников, – из n по m при всех m. Все сочетания из n по m при конкретном m = const соответствуют второй снизу строке (3). Одномерный аналог алгоритма дан в [6], детальное описание двумерного алгоритма – в [7].
Применение параллельной сортировки для упорядочения сочетаний и выбора оптимальной упаковки
Используется устойчивая [4] сортировка подсчетом одномерного массива (ниже – сортировка) на основе матрицы сравнений (МС) [3, 5]. Пусть по отношению «≤» требуется упорядочить элементы массива 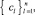 n < ∞. МС принимает вид [5]:
n < ∞. МС принимает вид [5]:
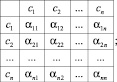
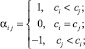 i = 1, 2, ..., n; j = 1, 2, ..., n. (5)
i = 1, 2, ..., n; j = 1, 2, ..., n. (5)
Значения αij из (5) удобно заменить символами «+», «0», «–», например, С = (6,1; 2,2; 7,6; 2,2; 7,3),
|
6,1 |
2,2 |
7,6 |
2,2 |
7,3 |
|
|
6,1 |
0 |
– |
+ |
– |
+ |
|
2,2 |
+ |
0 |
+ |
0 |
+ |
|
7,6 |
– |
– |
0 |
– |
– |
|
2,2 |
+ |
0 |
+ |
0 |
+ |
|
7,3 |
– |
– |
+ |
– |
0 |
Чтобы определить номер в отсортированном массиве j-го элемента входного массива, достаточно подсчитать число нулей и плюсов в j-м столбце над диагональю, включая диагональный элемент, и сложить это число с числом плюсов j-го столбца ниже диагонали. В обозначении отсортированного массива c1 получится: c1[3] = c[1]; c1[1] = c[2]; c1[5] = c[3]; c1[2] = c[4]; c1[4] = c[5]. Все сравнения в (5) взаимно независимы, инвертируют знак относительно диагонали, сортировка максимально параллельна с временной сложностью 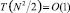 [3, 5]. Она сохраняет порядок равных элементов, является адресной с обратной адресацией на основе явного задания [3, 5] взаимно однозначного соответствия входных и выходных индексов. Сортировка будет применяться для максимально параллельного упорядочения элементов сочетаний и выбора оптимальной упаковки за минимальное время.
[3, 5]. Она сохраняет порядок равных элементов, является адресной с обратной адресацией на основе явного задания [3, 5] взаимно однозначного соответствия входных и выходных индексов. Сортировка будет применяться для максимально параллельного упорядочения элементов сочетаний и выбора оптимальной упаковки за минимальное время.
Описание алгоритма параллельной двумерной упаковки
Вначале алгоритм излагается на уровне содержательного описания.
Этап I. Задание веса элементов
I.1. Все прямоугольники фиксируются в последовательности, определяемой условием задачи, произвольно задается m = const, 1 < m < n.
I.2. Каждому прямоугольнику взаимно однозначно сопоставляется свой целочисленный вес. Конкретно, входные прямоугольники в порядке расположения нумеруются от единицы, i-му прямоугольнику присваивается вес i, i = 1, 2, ..., n. Выбираются первые
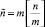 .
.
На данном этапе
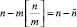
оставшихся номеров не будут подаваться на вход алгоритма генерации сочетаний, они группируются в отдельное сочетание (в дальнейшем – остаточное) и обрабатываются отдельно.
Этап II. Генерация и упаковка сочетаний
II.1. На основе (3) генерируются все сочетания из  по m. Остаточное сочетание рассматривается отдельно. Структура (3) сохраняется с заменой n на
по m. Остаточное сочетание рассматривается отдельно. Структура (3) сохраняется с заменой n на  , обуславливая обозначения:
, обуславливая обозначения: 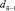 – все сочетания из
– все сочетания из  по 1,
по 1, 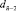 – все сочетания из
– все сочетания из  по
по 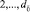 – сочетание из
– сочетание из  по
по  , xj ⊕ yj – размеры j-го прямоугольника,
, xj ⊕ yj – размеры j-го прямоугольника,  .
.
Матрицы из (3) имеют следующие особенности. Последний множитель справа – столбец, у которого верхний элемент равен единице, нижний – первый выбранный прямоугольник x0 ⊕ y0. Матрицы в (3) прямоугольные: число строк на единицу больше, чем число столбцов. Количество матриц соответствует количеству прямоугольников, на каждый прямоугольник приходится одна матрица.
Сочетания генерируются в соответствии последовательному умножению алгебраических матриц справа налево. Сначала преобразуются последняя и предшествующая ей матрица, в результате получится единственный столбец новой правосторонней матрицы с числом строк на единицу большим числа строк предшествующей правосторонней матрицы:
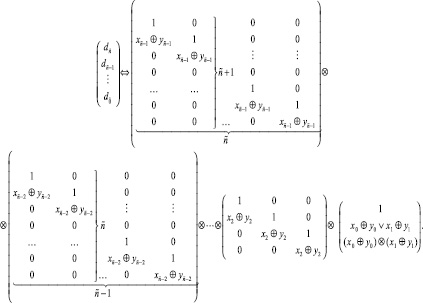
Полученная матрица из одного столбца и предшествующая ей слева матрица снова преобразуется соответственно алгебраическому умножению матриц. Получится матрица из одного столбца с числом строк на единицу большим матрицы-результата предыдущего шага. Преобразования выполняются до тех пор, пока не останется один результирующий столбец матрицы с числом строк, равным числу компонентов вектора в левой части (3).
II.2. В строке, сопоставленной 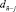 (кратко – в строке
(кратко – в строке 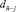 ), располагаются все сочетания элементов-прямоугольников из
), располагаются все сочетания элементов-прямоугольников из  по j, сочетания нумеруются в порядке расположения слева направо, начиная от единицы, число таких сочетаний есть
по j, сочетания нумеруются в порядке расположения слева направо, начиная от единицы, число таких сочетаний есть 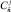 ,
, 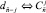 ,
, 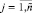 . В строке
. В строке 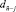 множество всех элементов всех сочетаний образует аналог двумерного массива – по своему индексу-весу в последовательности и по индексу номера сочетания в последовательности
множество всех элементов всех сочетаний образует аналог двумерного массива – по своему индексу-весу в последовательности и по индексу номера сочетания в последовательности 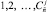 . Строка
. Строка 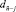 фиксируется при j = m, остальные строки на время изложения алгоритма не рассматриваются.
фиксируется при j = m, остальные строки на время изложения алгоритма не рассматриваются.
II.3. Выбор различных сочетаний из  по m, не содержащих общих элементов
по m, не содержащих общих элементов
II.3.1. У элементов строки 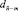 как аналога двумерного массива первый «индекс» – вес элемента (от единицы до
как аналога двумерного массива первый «индекс» – вес элемента (от единицы до  ) (фактически это не индекс, поскольку он может повторяться у элементов разных сочетаний, в сочетании это именно назначенный априори вес выбранного элемента). Второй индекс (он действительно индекс) – номер сочетания. Выполняется максимально параллельная сортировка всех
) (фактически это не индекс, поскольку он может повторяться у элементов разных сочетаний, в сочетании это именно назначенный априори вес выбранного элемента). Второй индекс (он действительно индекс) – номер сочетания. Выполняется максимально параллельная сортировка всех  элементов только по их весу: ключ, по которому выполняется сортировка, совпадает с весом элемента сочетания. Эта сортировка устойчива – сохраняет порядок равных элементов, поэтому все равные веса в отсортированном массиве расположатся друг за другом по неубыванию. Вторые индексы элементов переставятся вместе с элементами, так что элементы с равными весами, следуя подряд друг за другом, образуют вторыми индексами последовательность номеров (вообще говоря, неупорядоченную) различных сочетаний, в которые эти элементы входят.
элементов только по их весу: ключ, по которому выполняется сортировка, совпадает с весом элемента сочетания. Эта сортировка устойчива – сохраняет порядок равных элементов, поэтому все равные веса в отсортированном массиве расположатся друг за другом по неубыванию. Вторые индексы элементов переставятся вместе с элементами, так что элементы с равными весами, следуя подряд друг за другом, образуют вторыми индексами последовательность номеров (вообще говоря, неупорядоченную) различных сочетаний, в которые эти элементы входят.
II.3.2. Из последовательности, полученной в п. II.3.1, выбираются элементы, у которых первый «индекс» равен единице (вес i = 1). Каждому такому элементу сопоставляются элементы сочетания, в которое этот элемент входил, – в сочетание с ним объединяются элементы, имеющие одинаковый с ним второй индекс. Таким образом, данная операция восстанавливает сочетания, полученные априори.
Каждое выбранное сочетание оптимально упаковывается (синхронно и независимо друг от друга) каким-либо одним и тем же способом. После упаковки всех сочетаний с элементом единичного веса фиксируются окаймляющие прямоугольники каждого сочетания с минимальной вследствие упаковки площадью. После упаковки сохраняется второй (истинный) индекс сочетания. Все значения минимальных площадей сохраняются вместе со своими сочетаниями и параллельно сортируются по неубыванию с соответствующим смещением индекса сочетания. Получится неубывающая последовательность площадей окаймляющих сочетания прямоугольников, которые содержат элемент единичного веса.
Первый элемент отсортированной таким образом последовательности – наименьшая площадь, находящееся в нем упакованное сочетание идентифицируется по его второму индексу. Если у различных сочетаний, содержащих элемент единичного веса, площади окаймляющих прямоугольников равны, то согласно сортировке выбирается первое из этих сочетаний. Остальные сочетания с элементом единичного веса, соответствующие отсортированным площадям, удаляются из дальнейшего рассмотрения.
Для выбранного сочетания фиксируется его приоритетное местоположение. Учитывая единичный вес определившего сочетание элемента и второй его индекс, определивший все элементы сочетания, обозначим данное сочетание парой индексов (1, i1).
Способ исключения различных сочетаний с общими элементами заключается в следующем. Каждый из элементов сочетания (1, i1) попарно сравнивается по своему весу с элементами сочетаний соответственных отсортированной последовательности весов. Все сочетания с совпадающими по весу элементами, кроме (1, i1), удаляются из дальнейшего рассмотрения (в различных упакованных сочетаниях не должно быть одних и тех же прямоугольников). При этом адресация к каждому сочетанию и его идентификация при удалении выполняется по второму индексу элемента рассматриваемого веса.
Тем самым завершены все операции рассматриваемого способа с весом i = 1.
Далее, рассматривается линейка неудаленных весов. Все соответственные линейке отсортированных элементов сочетания обозначаются (k, ik), k ≥ 2. Рассмотрение выполняется для каждого веса k = const, ближайшего к рассмотренному и не удаленного на предыдущем шаге. Если неудаленных элементов с весом k несколько, то к линейке отсортированных элементов этого веса заново применяются все операции, описанные для (1, i1): предварительно выбираются все сочетания, содержащие вес k, и каждое такое сочетание отдельно упаковывается, выбирается сочетание с наименьшей окаймляющей площадью, оно фиксируется с приоритетом местоположения, а сравнение весов и удаление сочетаний будет теперь выполняться по отношению к сочетанию с элементом веса k. Аналогично, обрабатываются оставшиеся сочетания, элементы которых упорядочены по весу k, k ≥ 3. В результате выполнения последовательности данных шагов останется последовательность упакованных сочетаний прямоугольников с индексами (k, ik), 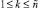 , среди которых некоторые значения k могут отсутствовать. Остаточное сочетание из
, среди которых некоторые значения k могут отсутствовать. Остаточное сочетание из 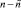 элементов подвергается упаковке синхронно с сочетаниями (1, i1).
элементов подвергается упаковке синхронно с сочетаниями (1, i1).
На выходе данного шага оказываются в наличии n прямоугольников, так как на входе были все возможные сочетания из  по m и остаточное сочетание из
по m и остаточное сочетание из 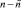 , а удалению подвергались лишь те из них, которые содержали общие элементы, так что остался набор сочетаний, включающий все попарно различные прямоугольники. Эти прямоугольники упакованы в сочетания, включая остаточное, общее количество которых составит
, а удалению подвергались лишь те из них, которые содержали общие элементы, так что остался набор сочетаний, включающий все попарно различные прямоугольники. Эти прямоугольники упакованы в сочетания, включая остаточное, общее количество которых составит 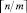 .
.
II.3.3. На выходе предыдущего шага получилась последовательность упакованных сочетаний (k, ik), 1 ≤ k ≤ n, включая остаточное, и окаймляющие эти сочетания прямоугольники минимизированной площади. Именно эти окаймляющие прямоугольники вместе с входящими в них упакованными элементами на входе следующего шага интерпретируются теперь как новые элементы для описанной обработки: они заново получают веса от единицы и второй индекс по сочетанию, сочетания генерируются по тому же алгоритму на основе формулы (3). Иными словами, по отношению к новым элементам (окаймляющим прямоугольникам) применяются этап I и шаги на нем I.1, I.2, затем этап II и шаги на нем II.1, II.2, II.3.1, II.3.2, II.3.3. Количество таких новых элементов равно [n/m].
Упаковка окаймляющих прямоугольников строится по числу не исключенных на предыдущем шаге входящих в них сочетаний. Таким образом, новые сочетания образуются из [n/m] по m элементов. После установления единственности сочетаний и попарно различных в них новых элементов на выходе последнего шага рассматриваемого этапа останется количество упакованных сочетаний равное 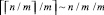 .
.
Формализация алгоритма
К первому шагу алгоритма относится вся совокупность описанных выше операций над входными элементами – прямоугольниками. Выходные данные первого шага (оптимизированные окаймляющие прямоугольники) полагаются входными элементами-прямоугольниками для второго шага, и ко второму шагу относится повторение всех операций первого шага над поступившими входными элементами. Выходные элементы второго шага («иерархически» оптимизированные окаймляющие прямоугольники) полагаются входными элементами для третьего шага, на котором воспроизводится аналогичная их обработка, и т.д. Процесс воспроизводится до тех пор, пока результат от деления в соотношении 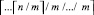 остается большим 1, – пока не получится единственный заключительный элемент («иерархически» оптимизированный по площади окаймляющий прямоугольник). Количество шагов алгоритма не превзойдет ~logmn.
остается большим 1, – пока не получится единственный заключительный элемент («иерархически» оптимизированный по площади окаймляющий прямоугольник). Количество шагов алгоритма не превзойдет ~logmn.
Оценки временной сложности
Временная сложность, обозначаемая T(R), где R – число процессоров, оценивается на модели неветвящихся параллельных программ без учёта обмена [8]. Поскольку 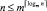 , число шагов формализованного алгоритма
, число шагов формализованного алгоритма 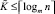 . Пусть
. Пусть  – временная сложность упаковки одного сочетания прямоугольников. С учетом максимального параллелизма используемой сортировки, числа шагов алгоритма и последовательности операций на шаге элементарным подсчетом получается оценка [7]:
– временная сложность упаковки одного сочетания прямоугольников. С учетом максимального параллелизма используемой сортировки, числа шагов алгоритма и последовательности операций на шаге элементарным подсчетом получается оценка [7]:
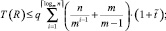
q = const; 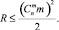
Отсюда
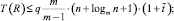
q = const; 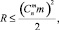 (6)
(6)
где не учитывается число процессоров для упаковки каждого сочетания из m прямоугольников. Таким образом, имеет место
Лемма 1. Двумерная упаковка на основе сортировки и видоизменения формул Виета может быть выполнена с помощью детерминированного параллельного алгоритма с временной сложностью (6).
Следствие 1. Глобально оптимальная упаковка получится при m = n.
При m ≠ n глобальный оптимум не является гарантированным, но наилучшая (локально оптимальная) упаковка достигается в каждом отдельном сочетании прямоугольников на каждом шаге.
Теорема 1. Если каждое сочетание из m прямоугольников упаковывается параллельным перебором всех 2m вариантов, то сохраняются утверждения леммы 1 и следствия 1, при этом временная сложность выполнения всего алгоритма составит
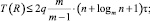
q = const; 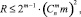 (7)
(7)
где τ – время бинарного сравнения, в оценке R учитывается число процессоров для максимально параллельной упаковки каждого рассматриваемого сочетания.
Следствие 2. Выполнение данного алгоритма параллельно по всем m < n даст выбор наилучшего по m из локально оптимальных вариантов упаковки с временной сложностью
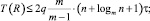
q = const; 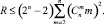
Следствие 3. Глобально оптимальная упаковка получится при m = n с временной сложностью,
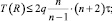
q = const; R ≤ (2n – 2)n2,
или T((2n – 2)n2) = O(n).
Следствие 4. При 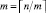 , или,
, или, 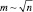 , упаковка заканчивается за 2 шага, и согласно (7)
, упаковка заканчивается за 2 шага, и согласно (7)
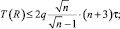
q = const; 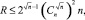
так что
T(R) = O(n); 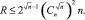
При этом все элементы каждого сочетания на первом шаге будут упакованы оптимально, равно как и на втором, однако глобальный оптимум на выходе алгоритма не является гарантированным.
Следствие 5. Если выполнять упаковку по алгоритму леммы 1, при этом по тому же алгоритму (а не перебором) выполнять упаковку каждого сочетания на текущем шаге, то временная сложность (6) перейдет в оценку
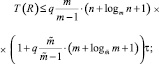
q = const; 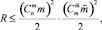
где 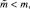
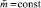 – число элементов сочетания из m по
– число элементов сочетания из m по  . В частности, при
. В частности, при 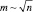 и
и 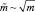 получится [7]:
получится [7]:
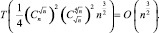
Последняя оценка означает, что время возрастает, сохраняя полиномиальный рост порядка 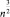 при снижении количества процессоров до
при снижении количества процессоров до
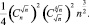
Такую рекурсивную вложенность алгоритма можно было бы продолжить, однако ввиду отсутствия гарантии глобального оптимума упаковки на выходе алгоритма целесообразность более глубоких рекурсивных вложений не очевидна.
Представленные оценки в явном виде не указывают временную сложность генерации сочетаний. Но число шагов (3) не больше n, на каждом шаге – не больше числа входных элементов на шаге, поэтому временная сложность параллельной генерации сочетаний на основе (3) с точностью до постоянного коэффициента не повлияет на значения порядков данных выше оценок.
Заключение
Представлен синтез и анализ параллельного детерминированного алгоритма двумерной упаковки. Алгоритм построен на основе устойчивой параллельной сортировки и видоизменения формул Виета восстановления коэффициентов полинома по его корням. Видоизменение использовано для параллельной генерации всех сочетаний прямоугольников из заданного конечного множества. Временная сложность алгоритма имеет полиномиальную оценку, близкую к линейной, выполняемая упаковка оптимальна в каждом сочетании на каждом последовательном шаге, но глобально оптимальной она оказывается лишь в случае экспоненциального роста числа процессоров.




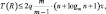 q = const, where
q = const, where 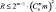 The work includes constructive description of parallel sorting algorithms, parallel generation of combinations of rectangles from n till m and parallel algorithm of the two-dimensional packaging based on them.
The work includes constructive description of parallel sorting algorithms, parallel generation of combinations of rectangles from n till m and parallel algorithm of the two-dimensional packaging based on them.