В современных инфокоммуникационных системах все большее применение находят параллельные вычислительные системы, расположенные на едином кристалле. Для обеспечения защиты информации от НСД в них, как правило, используют стандарт шифрования AES. Проведенный анализ работ [1–4] показал, что данный алгоритм шифрования подвергается различным криптоатакам, с целью его взлома и получения секретного ключа. Среди них особое место занимают криптоатаки, которые используют информацию, полученную по побочным каналам, в том числе на основе сбоев в работе шифратора. В результате проведения такой атаки злоумышленник, нарушая нормальную работу шифратора, вызывает ошибки в зашифрованном тексте, а затем на основе криптоанализа получает значение секретного ключа. Противостоять такому деструктивному воздействию можно за счет кодов, которые позволят обнаружить и исправить ошибки, вызванные сбоем в работе шифратора. Поэтому разработка алгоритма поиска и исправления ошибок с использованием полиномиальной системы классов вычетов (ПСКВ), которая полностью соответствует математической основе алгоритма шифрования AES, является актуальной задачей.
Современные системы на кристалле (СнК) объединяют на кристалле помимо нескольких процессорных ядер общего назначения еще и специализированные вычислительные модули. Так, в чипах Marvell Armada и TI OMAP [5] на одном чипе объединяются процессорные модули и криптографический ускорители. Так, для обеспечения конфиденциальности передаваемой информации в микропроцессорах Sitara Am38x, которые предназначены для использования в приборах и системах управления промышленной, введен криптопроцессор [6].
Одним из наиболее часто используемых алгоритмов криптозащиты является алгоритм шифрования AES. Это связано с тем, что данный алгоритм имеет лучшее сочетание криптографической стойкости, производительности, эффективности реализации и гибкости. В качестве достоинств алгоритма шифрования AES можно выделить высокий уровень защищенности, реализацию в smart-картах благодаря низким требованиям к объемам памяти, высокую эффективность на любых платформах [7].
Широкое применение стандарта шифрования AES стимулировало большое число атак на данный алгоритм, которые делятся на следующие группы. Основу первой группы составляют «классические атаки» на алгоритм шифрования. В работе [1] показано проведение атаки методом бумеранга на 6-раундовую версию алгоритма со 128-битным ключом.
Вторая группа криптоатак базируется на модификации различных методов криптоанализа на связанных ключах. Так комбинация метода бумеранга и связанных ключей способствовала проведению атаки на 10 из 12 раундов алгоритма AES-192 [2].
Третья группа криптоатак на алгоритм шифрования AES·связаны с попытки использования алгебраических свойств алгоритма для его вскрытия. Такие атаки относятся к «алгебраическим атакам» [3].
В четвертую группу можно отнести исследования, которые посвящены атакам, использующим информацию, полученную по побочным каналам (side-channel-атакам). Особое место среди криптоатак по побочным каналам занимает атака на основе сбоев [4]. Эта атака относится к активным атакам. Эти атаки возможны в условиях, когда на шифрующее устройство осуществляются различные воздействия с целью внести искажения в информацию на различных этапах шифрования. В качестве защиты от атаки используют добавление в шифрующий механизм датчиков воздействий, блокирующих шифратор при ненормальных параметрах системы, вычисление контрольной суммы, экранирование шифратора.
Однако данные способы не учитывают особенности алгоритма шифрования, что приводит к значительным затратным решениям, в том числе и для блочного шифра AES. Поэтому разработка алгоритма, позволяющего противодействовать такой атаке путем обнаружения и коррекции возникшей ошибки в процессе шифрования, является актуальной задачей. Для противодействия атакам на основе сбоев в алгоритме AES предлагается использовать полиномиальную систему классов вычетов.
Известно, что алгоритм шифрования AES использует математический аппарат поля Галуа GF(28) с порождающим полиномом m (x) = x8 + x4 + x3 + x + 1. При этом алгоритм оперирует байтами, которые рассматриваются как элементы конечного поля GF(28). Если в качестве информационных оснований ПСКВ использовать неприводимые полиномы 4 степени, то есть m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1, то операции в поле GF(28) можно заменить аналогичным операциями в полях меньшей размерности GF(24). Следовательно, при реализации алгоритма шифрования AES можно эффективно использовать полиномиальную систему классов вычетов с двумя основаниями m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1.
Как показано в работах [8–10], ПСКВ позволяет организовать вычисления параллельно, помодульно и независимо друг от друга, так как операции сложения, вычитания и умножения сводятся к соответствующим операциям над остатками по модулям pl(z) над полем:
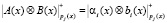 , (1)
, (1)
где 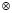 – операции сложения, вычитания и умножения в GF(p); А(х) = (α1(х), α2(х),...,αk(x)) и B(х) = (b1(х), b2(х),...,bn(x));
– операции сложения, вычитания и умножения в GF(p); А(х) = (α1(х), α2(х),...,αk(x)) и B(х) = (b1(х), b2(х),...,bn(x)); 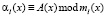 ;
; 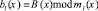 ; l = 1, …, k.
; l = 1, …, k.
Известно, что операции, которые реализуются в блоке замены байтов – преобразователе SubBytes алгоритма AES, представляют собой совокупность операций умножения и сложения по модулю. Значит, данные операции можно эффективно реализовать в полиномиальной системе классов вычетов.
Кроме того, коды ПСКВ позволяют обнаруживать и корректировать ошибки, которые возникают в процессе работы вычислительного устройства из-за отказа и сбоев оборудования [9, 10]. Для решения данной задачи в набор информационных оснований ПСКВ вводятся дополнительные контрольные основания. При реализации алгоритма шифрования на основе ПСКВ предлагается использовать в качестве рабочих оснований следующие полиномы m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1. Использование данных полиномов позволяет обеспечить рабочий диапазон, степень которого будет равна восьми. В качестве контрольного основания выбираем полином m3(x) = x4 + x3 + x2 + x + 1. Применение одного контрольного основания ПСКВ позволяет обнаруживать факт наличия ошибок, вызванных сбоями в работе устройства.
Повысить эффективность противодействия сбоям в работе алгоритма AES можно за счет алгоритма коррекции, который приведен в работе [9]. В работе [10] приведена схемная реализация этого алгоритма. Для реализации процесса обнаружения и исправления ошибок в модулярном коде полинома 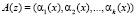 вводят избыточность. С этой целью выбирается одно контрольное основание mk + 1(x), удовлетворяющее условию
вводят избыточность. С этой целью выбирается одно контрольное основание mk + 1(x), удовлетворяющее условию
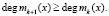 (2)
(2)
При этом использовании данного контрольного модуля можно однозначно исправить однократную ошибку. Под однократной ошибкой понимается искажение одного разряда в кодовой комбинации, представленной в ПСКВ. Для этого необходимо провести вычисления:
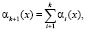 (3)
(3)
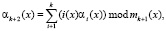 (4)
(4)
где i(x) – полиномиальная форма i-го порядкового номера, Σ – слоение по модулю два.
Для обнаружения ошибки в переданной кодовой комбинации вычисляются значения
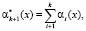 (5)
(5)
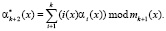 (6)
(6)
Значения 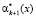 и
и 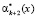 используются для вычисления синдрома ошибки:
используются для вычисления синдрома ошибки:
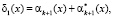 (7)
(7)
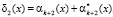 . (8)
. (8)
Если синдром ошибки δ1(х) = 0 и δ2(х) = 0, то комбинация не содержит ошибки. В противном случае, когда δ1(х) ≠ 0 и δ2(х) ≠ 0, комбинация является запрещенной, т.е. ошибочной. По величине δ1(х) и δ2(х) можно провести коррекцию однократной ошибки.
Рассмотрим применение избыточной ПСКВ при реализации базовой процедуры замены блоков в алгоритме шифрования AES. Байт открытого текста S поступает на вход преобразователя из позиционного кода в код ПСКВ, с выхода которого снимаются значения двух остатков s1(x) и s2(x), где 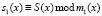 и
и 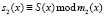 . Таким образом, текущий байт представляет S(x) собой два четырехразрядных блока данных. В таком виде данные поступают на входы преобразователя SubBytes. При этом первый остаток s1(x) определяет номер столбца, а номер строки задается остатком по второму модулю s2(x). В этом случае таблица замен SubBytes, которая требовала блок памяти 256×8 бит, теперь представляется в виде двух таблиц размером 256×4 бит. Каждая из таблиц представляет собой остаток числа результата подстановки
. Таким образом, текущий байт представляет S(x) собой два четырехразрядных блока данных. В таком виде данные поступают на входы преобразователя SubBytes. При этом первый остаток s1(x) определяет номер столбца, а номер строки задается остатком по второму модулю s2(x). В этом случае таблица замен SubBytes, которая требовала блок памяти 256×8 бит, теперь представляется в виде двух таблиц размером 256×4 бит. Каждая из таблиц представляет собой остаток числа результата подстановки 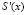 , приведенной по модулям m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1 соответственно. В табл. 1 приведены первые три строки таблицы замен S1-блока по рабочему модулю m1(x) = x4 + x + 1.
, приведенной по модулям m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1 соответственно. В табл. 1 приведены первые три строки таблицы замен S1-блока по рабочему модулю m1(x) = x4 + x + 1.
В табл. 2 приведены первые три строки таблицы замен S2-блока по модулю m2(x) = x4 + x3 + 1 соответственно.
Пусть байт открытого текста равен S(x) = {000110012}={1916}. Данное значение поступает на вход преобразователя из позиционного кода в ПСКВ, с выхода которого будут сниматься два остатка:
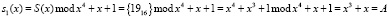
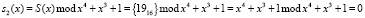 .
.
Таким образом, на входы каждой из таблиц замен S1-блока по модулю m1(x) = x4 + x + 1 и S2-блока по модулю m1(x) = x4 + x3 + 1 поступают остатки S(x) = (А, 0). Результат замены определяется из табл. 1 и 2. В табл. 1 на пересечении столбца А и строки 0 находится число 0. В табл. 2 на пересечении столбца А и строки 0 находится число 5. В результате воздействия на байт состояния S(x) = {000110012}={1916}=(А, 0) был получен байт подстановки, который в ПСКВ по этим двум основаниям представляется в виде двух остатков S’(x) = (0, 5). Полученный результат соответствует подстановке S’(x) = ={d416}={110101002}. Это подтверждается следующими сравнениями:
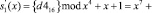
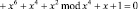 ;
;
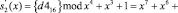
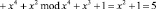 .
.
Для реализации противодействия атакам, построенных на сбоях работы шифратора, используются дополнительно табл. 3 и 4. Табл. 3 содержит данные о сумме остатков информационных оснований ПСКВ m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1. Результат был получен на основе равенства (3).
Таблица 1
Таблица замен S1-блока по модулю m1(x) = x4 + x + 1
|
s2(x) |
Остаток s1(x) по модулю m1(x) = x4 + x + 1 |
|||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
9 |
9 |
2 |
F |
D |
B |
B |
5 |
B |
F |
0 |
1 |
4 |
3 |
F |
9 |
|
1 |
D |
5 |
9 |
0 |
9 |
3 |
4 |
A |
4 |
F |
6 |
0 |
4 |
8 |
9 |
1 |
|
2 |
A |
2 |
E |
5 |
A |
4 |
6 |
C |
2 |
4 |
D |
6 |
6 |
D |
F |
8 |
Таблица 2
Таблица замен S2-блока по модулю m1(x) = x4 + x + 1
|
s2(x) |
Остаток s1(x) по модулю m1(x) = x4 + x + 1 |
|||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
7 |
F |
8 |
3 |
5 |
C |
B |
8 |
6 |
4 |
5 |
4 |
E |
B |
C |
B |
|
1 |
B |
1 |
4 |
6 |
D |
9 |
B |
F |
D |
F |
A |
1 |
6 |
B |
C |
2 |
|
2 |
2 |
0 |
A |
7 |
F |
4 |
3 |
2 |
3 |
5 |
E |
B |
1 |
9 |
9 |
9 |
Таблица 3
Остатки α3(х) по модулю m3(x) = x4 + x3 + x2 + x + 1
|
s2(x) |
Остаток s1(x) по модулю m1(x) = x4 + x + 1 |
|||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
E |
6 |
A |
C |
8 |
7 |
0 |
D |
D |
B |
5 |
5 |
A |
8 |
3 |
2 |
|
1 |
6 |
4 |
D |
6 |
4 |
A |
F |
5 |
9 |
0 |
C |
1 |
2 |
3 |
5 |
3 |
|
2 |
8 |
2 |
4 |
2 |
5 |
0 |
5 |
E |
1 |
1 |
3 |
D |
7 |
4 |
6 |
1 |
Таблица 4
Остатки α4(х) по модулю m3(x) = x4 + x3 + x2 + x + 1
|
s2(x) |
Остаток s1(x) по модулю m1(x) = x4 + x + 1 |
|||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
7 |
E |
B |
9 |
7 |
A |
4 |
C |
7 |
7 |
A |
9 |
1 |
C |
E |
6 |
|
1 |
2 |
7 |
1 |
C |
A |
8 |
B |
D |
7 |
8 |
B |
2 |
8 |
7 |
8 |
5 |
|
2 |
E |
2 |
3 |
B |
D |
C |
0 |
8 |
4 |
E |
8 |
9 |
4 |
6 |
4 |
3 |
В табл. 4 представлены данные о взвешенной сумме остатков рабочих оснований m1(x) = x4 + x + 1 и m2(x) = x4 + x3 + 1. Результат был получен на основе равенства (4).
Таким образом, при подаче на вход табл. 3 и 4 значений остатков S(x) = (А, 0) с выхода табл. 3 будет снято значение {516} = {01012} = {х2 + 1}. Данное число находится на пересечении столбца А и строки 0 в табл. 3. С выхода табл. 4 будет снято значение {А16} = {10102} = {х3 + х}.
Пусть в процессе работы шифратора AES атак не проводилось. Тогда после выполнения операции подстановки проводится проверка на наличие ошибок в комбинации ПСКВ:
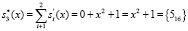 .
.
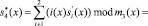
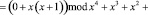
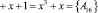 .
.
Затем, согласно (7) и (8), производится вычисление синдрома ошибки. Так как синдром равен нулю, то сбоя в процессе работы шифратора не произошло. Полученные значения остатков 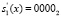 и
и 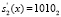 по рабочим основаниям ПСКВ дальше будут участвовать в последующих раундовых преобразованиях, побайтовом сдвиге строк Shift Rows, перемешивании столбцов MixColums сложении с раундовым ключом AddRoundKey.
по рабочим основаниям ПСКВ дальше будут участвовать в последующих раундовых преобразованиях, побайтовом сдвиге строк Shift Rows, перемешивании столбцов MixColums сложении с раундовым ключом AddRoundKey.
Пусть в процессе работы шифратора произошла атака на основе сбоев. Сбой вызвал изменение остатка по основанию m1(x) = x4 + x + 1, а его глубина равна Δs1(x) = 1. Тогда
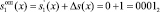 .
.
В результате на вход блока, реализующего алгоритм коррекции ошибок, подается
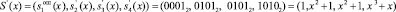 .
.
Тогда вычисленные новые значения проверочных остатков, согласно (5) и (6), равны
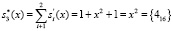 .
.
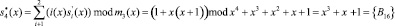 .
.
Затем производится вычисление синдрома ошибки
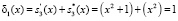 .
.
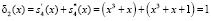 .
.
Так как синдром ошибки не равен нулю, то это свидетельствует о том, что в ходе выполнения раундового преобразования произошел сбой. Тогда, зная местоположение ошибки и ее глубину, можно провести коррекцию
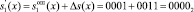 .
.
Таким образом, благодаря разработанному алгоритму коррекции ошибок с использованием ПСКВ можно устранять последствия сбоев в работе шифратора алгоритма AES.
Выводы
Для противодействия атакам на основе сбоев был разработан алгоритм коррекции ошибок с использованием кодов ПСКВ. При этом переход от работы в поле Галуа GF(28) к полям Галуа GF(24) позволяет корректировать ошибки при меньших схемных затратах. Использование алгоритма обеспечивает исправление всех однократных ошибок и до 80 процентов двукратных ошибок, возникающих из-за сбоев в работе шифратора. При этом требуется в 1,22 раза меньше схемных затрат по сравнению с классической системой маскирования отказов «2 из 3». Полученные результаты свидетельствуют об эффективности применения кодов ПСКВ для противодействия последствиям атак на основе сбоев.



