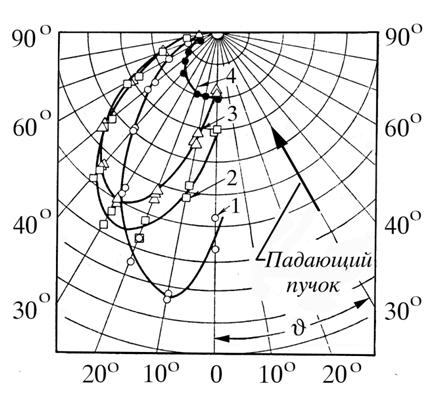
Рис. 1. Угловое рассеяние аргона никелем NiIII.: 1 - tNi=510 oC; tAr=20 oC, 2 - tNi=510 oC; tAr=1310 oC, 3 - tNi=510 oC; tAr=2450 oC, 4 - tNi=20 oC; tAr=20 oC.
На самом деле аналитически точно решить данную задачу не представляется возможным, если индикатриса рассеяния описывается законом Кнудсена. Проблему создает многократное рассеяние молекул, с одной стороны, дающее существенный вклад в давление, с которым газ действует на тело, а с другой стороны, делающее аналитическое рассмотрение практически недоступным. Имеет смысл рассмотреть сначала более скромную задачу, то есть предположить, что все молекулы рассеиваются в направлении, перпендикулярном поверхности. По тем же причинам целесообразно рассмотреть наиболее простой характер шероховатости поверхности, кстати говоря, допускающий рассмотрение только однократных столкновений молекул газа, если α<π/4 (рис. 2).
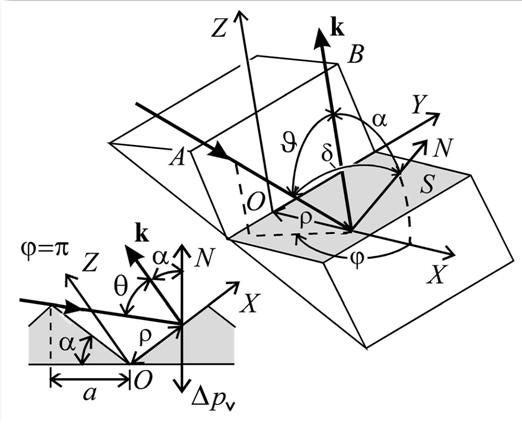
Рис. 2. Геометрия диффузного рассеяния газа шероховатой поверхностью
В данную точку P поверхности S попадают только те молекулы, направления движения которых заключены в интервале углов 0<υ<θ, где угол θ определяется исходя из следующих соображений. Уравнение траектории движения молекулы до рассеяния имеет вид
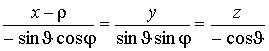 . (1)
. (1)
С другой стороны для ребра AB справедливы соотношения
![]() . (2)
. (2)
Поэтому, угол θ, соответствующий движению молекулы с вершины клина, определяется выражением
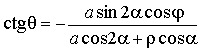 . (3)
. (3)
Распределение молекул по направлениям считается изотропным. Поэтому за интервал времени dt элемента площади dydr достигнет
![]() (4)
(4)
молекул, движущихся в интервале углов от u до u+du и отφ до φ+dφ. Здесь dnv - число молекул, чьи скорости заключены в интервале от v до v+dv, и dΩ=sinududφ. Каждая молекула в результате столкновения передает телу импульс p-kp, где вектор k направлен по нормали к рассеивающей поверхности (см. рис. 2). Следовательно вертикальная составляющая этого импульса равна
![]() , (5)
, (5)
а вертикальная компонента силы, действующей на элемент площади dydρ, составляет величину
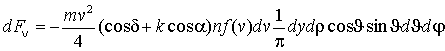 , (6)
, (6)
где f(v) - функция распределения молекул по скоростям, n - их плотность. При -π/2<φ<π/2 соседняя грань не является помехой движению, поэтому в этом случае угол u изменяется в пределах 0
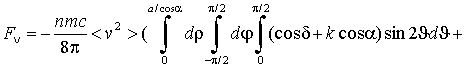
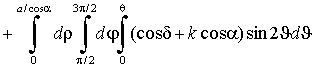 (7)
(7)
где угол δ между траекторией первичной частицы и вертикалью N зависит от переменных u и φ:
![]() . (8)
. (8)
Интегрирование (7) утомительно, но элементарно, однако приводит к следующему неожиданному результату:
![]()
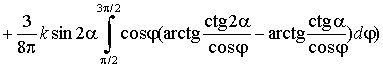 . (9)
. (9)
Совершенно очевидно, что частный случай α=0 с одновременной переменой знака соответствует силе, с которой атмосфера действует на часть основания призмы шириной a:
![]() . (10)
. (10)
При k=2/3 это совпадает с результатом вывода уравнения идеального газа, основанного на предположении зеркального рассеяния молекул [7]. Однако, выбор такого значения коэффициента k, вообще говоря, противоречит закону сохранения энергии, поскольку означает нагрев твердого тела, что изначально не предполагалось. Вполне разумным является выбор k=1, требующий, правда, пересмотра интерпретации абсолютной температуры; для данного наполовину качественного рассмотрения это не столь важно. В конечном итоге абсолютная температура - это обратная производная от энтропии тела по его энергии [8]. Для одной и той же температуры изменения энтропии, сопровождающие зеркальное и диффузное отражения, - разные.
Цель настоящей работы - продемонстрировать, что диффузное рассеяние в совокупности с экранированием, обусловленным шероховатостью одной поверхности, должно приводить к появлении отличной от нуля силы, действующей на все тело. Чтобы оценить величину этой силы, достаточно вычислить отношение (F^+Fv)/F^ и вспомнить, что на каждый квадратный метр поверхности атмосфера давить с силой порядка 105 Н. Зависимость это относительной подъемной силы от угла a показана на рис. 3 и, к сожалению, создает проблему в понимании. Остается вопрос, с которым следует обязательно разобраться: подъемная сила оказалась слишком большой. Понятно, что подавляющую часть этой силы следует списать на дефект модели расчета: индикатриса рассеяния заменена дельта-функцией. Но даже если реальная подъемная сила окажется в десять-сто раз меньше, это будет вполне достаточно, чтобы позаботиться об экспериментальной проверке результата. При этом необходимо подчеркнуть одно обстоятельство: характерный размер шероховатости должен быть значительно меньше длины свободного пробега молекул в воздухе, то есть 10-7 м. В противном случае какой либо разговор об экранировании, обусловленном шероховатостью, теряет смысл. Нет оснований и сомневаться в реальности диффузного рассеяния молекул газа поверхностью твердого тела. В ряде случаев оно действительно имеет место. Важно отметить, что не существует значения коэффициента k, при котором дефицит силы оказался бы равным нулю. Здесь нет противоречия, с одной стороны увеличение этого коэффициента приводит к возрастанию силы, направленной вниз, а с другой стороны, при этом увеличивается сила, с которой атмосфера давит на не шероховатую поверхность твердого тела. Другое дело, что нечто другое, возможно полностью компенсирующее дефицит силы, действующей сверху, не учитывалось в данном классическом расчете, а это, в свою очередь, является вполне обоснованным поводом для активизации исследований процессов взаимодействия газа с твердыми телами.
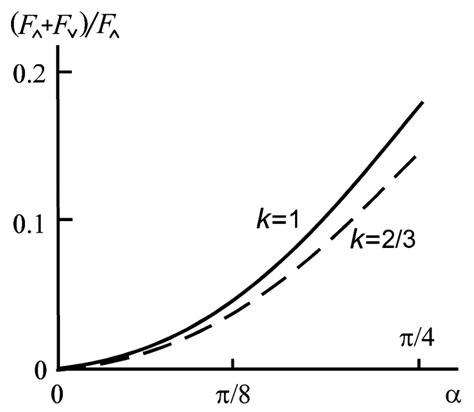
Рис. 3. Зависимость относительной подъемной силы от угла наклона граней шероховатой поверхности
СПИСОК ЛИТЕРАТУРЫ
- Smith J.N., Fite W.L. Recent Investigation of Gas-Surface Interactions Using Modulated-Atomic-Beam Techniques. // Proceedings of the Third International Symposium on Rarefield Gas Dynamics. 1963. V. 1. P. 430-453.
- Гудман Ф., Вахман Г. Динамика рассеяния газа поверхностью. М.: Мир, 1980. 424 с.
- Герасимов С.А. О левитации и экранировании в газовой динамике. // Вопросы прикладной физики. 2005. № 12. С. 131-133.
- Герасимов С.А. Задача об упругом многократном рассеянии и термолевитации. // Учебная физика. 2005. № 2. С. 71-80.
- Герасимов С.А. Первое начало термолевитации. // Успехи современного естествознания. 2008. № 8. С. 118-119.
- Бешок М.П. Энергия воздуха. // Новая энергетика. 2003. № 4. С. 31-32.
- Савельев И.В. Курс общей физики. Механика и молекулярная физика. М.: Наука, 1977. 416 с.
- Ландау Л.Д., Лифшиц Е.М. Статистическая физика. М.: Наука, 1976. 584 с.



