Ниже излагается обобщенное решение кинематических задач о круглых цилиндре и шаре, движущихся произвольным образом (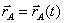
,
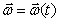) в безграничном потоке идеальной несжимаемой жидкости, имеющем на бесконечности скорость 
.
Принимается, что поле скоростей безвихревое (
), потенциал скоростей φ удовлетворяет уравнению Лапласа 
( Δ -оператор Лапласа) и для всех точек поверхностей тел S должно выполняться условие 
, где 
. (1)
Для цилиндра, совершающего плоское движение ортогонально своей оси, достаточно рассмотреть движение круглого его сечения радиуса a в его плоскости, принимаемой за плоскость xOy, использовать комплексную координату Z =x + iy и комплексный потенциал скоростей 
являющийся аналитической функцией аргумента Z. Комплексно сопряженная скорость частицы жидкости определяется по формуле 
.
Простейшие комплексные потенциалы:
(поступательный поток), 
(точечный источник q>0 (сток <0)), 
(вихрь. Г - вещественное), 
(диполь). (2)
Вывод формулы для комплексного диполя
Поместим в начало координат сток, обильности q, а источник такой же обильности - в точку с координатой 
. Комплексный потенциал скоростей, порожденный этой гидродинамической системой в произвольной точке с комплексной координатой Z, равен
Запишем эту формулу так
и перейдем в ней к пределу при условиях: 
, 
. Так как 
, то получаем 
что подтверждает справедливость формулы (2).
Простейшие пространственные потенциалы (r¯ - радиус-вектор точки):
(поступательный поток),
(пространственный точечный источник, q>0 (сток, q<0)), 
(пространственный диполь) (3)
Вывод формулы для пространственного диполя
Размещаем в начале координат сток обильности q, а источник равной обильности - в точке 
. Потенциал скоростей, порожденный этой системой в точке с векторной координатой r¯, равен
Запишем эту формулу так: 
.
Потенциал пространственного диполя φ определяется как предел потенциала φ* при условиях:
, 
,
,
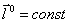. Учитываем, что 
- производная по направлению 
), 
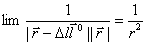В результате получаем 
, что полностью согласуется с формулой (3).
Потенциалы скоростей, порожденные движением цилиндра и шара в жидкости
Так как идеальная жидкость не имеет внутреннего трения, то вращения цилиндра вокруг своей оси и шара не оказывают никакого влияния на движение такой жидкости и на поле скоростей в ней. Поэтому при построении потенциала скоростей, порожденных движением этих тел, учитываем .только их поступательное движение со скоростью u¯.
Для цилиндра искомый комплексный потенциал w представляем в таком виде
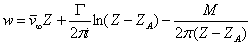(4)
где А - центр сечения. Комплексно сопряженная скорость потока равна
(5)
Условия на бесконечности удовлетворены. Распорядимся выбором величин Г и М так, чтобы выполнялось условие (1), приводящее к равенству 
, где 
. Так как на L 
, то 
, что приводит к равенству
Re[(
. из которого следует, что циркуляция Г остается неопределенной, а момент диполя, входящего в формулы (4) и (5), равен
(6)
Для шара радиуса a с центром в точке А принимаем 
,
и
(7)
Так как , то в потоке
(8)
Учитываем, что на поверхности шара 
и 
и выполняем условие (1). Получаем равенство
, или 
,
Вектор 
не постоянен, поэтому последнее равенство возможно лишь при
При этом значении M¯ и , для шара справедливы формулы (7) и (8).
Список литературы
- Лойцянский Л.Г.Механика жидкости и газа. - М., 1973. 817 с.
- Кочин Н.Е., Кибель И.Я., Розе Н.В. Теоретическая гидромеханика. М., 1963. Т. 1, 586 с.
- Валландер С.В. Лекции по гидроаэромеханике. Л., Издательство ЛГУ, 1978, 286 с.
- Batchelor G.K. An Introduction to Fluid Dinamics. Cambridge University. 2000. 631 pp.
Библиографическая ссылка
А.И. Снопов ПОТЕНЦИАЛЫ СКОРОСТЕЙ, ПОРОЖДАЕМЫЕ КРУГЛЫМИ ЦИЛИНДРОМ И ШАРОМ В ПОТОКЕ ЖИДКОСТИ // Современные наукоемкие технологии. 2010. № 7. С. 321-324;URL: https://top-technologies.ru/ru/article/view?id=25150 (дата обращения: 03.04.2025).