В настоящее время в ИГиП ДВО РАН разрабатываются фторидно-аммониевые технологии переработки минерального сырья Верхнего Приамурья [1; 2]. К ценному минеральному сырью приравниваются золошлаковые отходы ТЭЦ, содержащие многие полезные компоненты, включая оксиды алюминия, железа и кремния, редкие элементы и благородные металлы. В процессе отработки технологий проводятся как предварительные расчеты вероятных направлений химических реакций, так и компьютерная обработка экспериментов по топохимической кинетике [3]. В данной статье выполняется математическая обработка кинетики фторирования гидродифторидом аммония (ГДФА) золы из Золоотвала Благовещенской ТЭЦ (ЗБТЭЦ), применяется и усовершенствуется разрабатываемая методика расчетов по топохимической кинетике.
Отправной точкой исследований по топохимической кинетике являются массивы значений степеней превращения исследуемого вещества в последовательные отсчеты времени и исследуемых температур. В ходе компьютерной обработки рассчитываются значения ряда кинетических параметров реакций. Функция отклика, например, позволяет вычислить вероятное значение степени превращения продукта реакции в произвольный момент времени. Количественные знания о ходе реакции позволяют сравнивать её с аналогичными реакциями, как изучавшимися нами ранее, так и встречающимися в литературе, с целью выбора физико-химических условий комплексной переработки, включая выбор конкретной химической реакции на каждой стадии и оптимальных условий её протекания.
Материалы и методы исследования
Методы исследования в данной работе – параметрический регрессионный и корреляционный анализы [4; 5]. Учитывая вид кинетических кривых в экспериментах по фторированию алюмосиликатов, выберем в качестве параметрических функций часто используемые для описания топохимических реакций уравнения: степенной (i = 0) и экспоненциальный (i = 2) законы, являющиеся уравнениями ускоряющегося типа
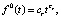 (1)
(1)
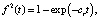 (2)
(2)
а также уравнение Ерофеева-Авраами (i = 1) сигмоидного типа
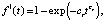 (3)
(3)
где 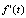 – i-я параметрическая функция времени, сr и cs – константа скорости и коэффициент формы кинетической кривой, соответственно [6].
– i-я параметрическая функция времени, сr и cs – константа скорости и коэффициент формы кинетической кривой, соответственно [6].
На основе параметрических функций строим регрессионные модели. Нелинейность параметрических функций обусловливает нелинейность регрессионных моделей. Линейную регрессионную модель для i-й параметрической функции получим после проведения замен переменных 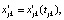
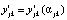 аналогично [3]
аналогично [3]
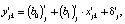 (4)
(4)
где i, j и k – индексы регрессионной модели, исследуемой температуры и отсчета времени, соответственно (i = 0, 1, 2; j = 0, 1,…, mj; k = 0, 1,…, nj); 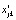 и
и 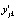 ; mj и nj, tjk и αjk,
; mj и nj, tjk и αjk, 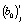 и
и 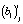 ,
, 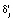 – значения -х обобщенных абсциссы и ординаты, количество исследуемых температур и отсчетов времени, отсчет времени и степень превращения вещества, первый и второй коэффициенты линейной регрессии, ошибка эксперимента для i-й регрессионной модели, соответственно, в момент отсчета времени tjk при температуре Tj.
– значения -х обобщенных абсциссы и ординаты, количество исследуемых температур и отсчетов времени, отсчет времени и степень превращения вещества, первый и второй коэффициенты линейной регрессии, ошибка эксперимента для i-й регрессионной модели, соответственно, в момент отсчета времени tjk при температуре Tj.
Точечные оценки 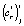 и
и 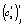 для i-й регрессионной модели при температуре Tj параметров сr и cs, соответственно, вычисляются согласно (3) из оценок коэффициентов регрессии
для i-й регрессионной модели при температуре Tj параметров сr и cs, соответственно, вычисляются согласно (3) из оценок коэффициентов регрессии 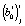 и
и 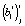 , которые, в свою очередь, рассчитываются методом наименьших квадратов по уравнению (4). После подстановки точечных оценок параметров
, которые, в свою очередь, рассчитываются методом наименьших квадратов по уравнению (4). После подстановки точечных оценок параметров 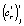 и
и 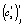 в i-ю параметрическую функцию получим i-ю функцию отклика для температуры Tj
в i-ю параметрическую функцию получим i-ю функцию отклика для температуры Tj
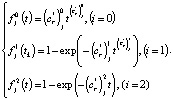 (5)
(5)
Энергию активации Ei для i-й модели регрессии вычисляют по уравнению Аррениуса для констант скоростей i-й модели (6) [7]. При этом в качестве независимой компоненты выступает обратная температура, а в качестве случайной функции – логарифм константы скорости, возникающий после логарифмирования этого уравнения
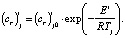 (6)
(6)
Погрешности кинетических параметров рассчитывались согласно [3] в соответствии с методикой [4].
Выбор между моделями регрессии при каждой температуре предварительно выполняем по минимуму погрешностей аппроксимаций [4], которые рассчитываются по формуле
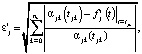 (7)
(7)
где αjk(tjk) и 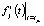 – экспериментальные значения степени превращения вещества и расчетные значения i-й функции отклика
– экспериментальные значения степени превращения вещества и расчетные значения i-й функции отклика 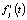 в момент времени tjk, nk – количество отсчетов времени. После проведения предварительного выбора модели реакции при данной температуре по погрешностям аппроксимаций и последующего расчета кинетических характеристик проводится статистическая проверка гипотез регрессионного анализа, по окончании которой может быть скорректирован выбор модели.
в момент времени tjk, nk – количество отсчетов времени. После проведения предварительного выбора модели реакции при данной температуре по погрешностям аппроксимаций и последующего расчета кинетических характеристик проводится статистическая проверка гипотез регрессионного анализа, по окончании которой может быть скорректирован выбор модели.
С целью проверки пяти статистических гипотез, использующихся в работе, рассчитывается ряд соответствующих статистик. Статистики используются для проверки допустимости применения регрессионного анализа, адекватности выбранных регрессионных моделей, значимости их коэффициентов. Практическую ценность регрессионная модель имеет при наличии достаточно сильной линейной связи между входными и выходными данными, при которой коэффициент корреляции и показатель согласованности Стьюдента достаточно велики.
С целью исследования вопроса о допустимости применения регрессионного анализа проводится проверка однородности дисперсии. В качестве нулевой гипотезы принимается гипотеза о равенстве дисперсий воспроизводимости в каждой точке факторного пространства. Статистическая проверка этой гипотезы выполняется методом Снедекора-Фишера. Сначала рассчитываются оценки дисперсий воспроизводимости 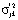 в каждой точке (tjk, αjk) факторного пространства путем проведения ljk измерений, затем строится F-отношение максимальной и минимальной дисперсии
в каждой точке (tjk, αjk) факторного пространства путем проведения ljk измерений, затем строится F-отношение максимальной и минимальной дисперсии 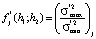 по всему факторному пространству при температуре Tj. Критическое значение fβ(h1; h2) выбирается по таблице F-распределения на уровне значимости β и числа степеней свободы h1 и h2 для
по всему факторному пространству при температуре Tj. Критическое значение fβ(h1; h2) выбирается по таблице F-распределения на уровне значимости β и числа степеней свободы h1 и h2 для 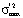 и
и 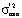 , соответственно. Гипотеза об однородности принимается, если
, соответственно. Гипотеза об однородности принимается, если
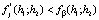 . (8)
. (8)
Для проверки адекватности модели при помощи F-отношения Снедекора-Фишера сравниваются остаточная 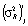 и общая дисперсия воспроизводимости
и общая дисперсия воспроизводимости 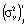 . Первая вычисляется по формуле
. Первая вычисляется по формуле 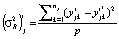 , где
, где 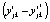 – отклонения значений обобщенной ординаты
– отклонения значений обобщенной ординаты 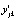 в точке tjk от её значений
в точке tjk от её значений 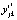 в этой точке по уравнению регрессии (4), p – число степеней свободы. Вторая – по формуле
в этой точке по уравнению регрессии (4), p – число степеней свободы. Вторая – по формуле 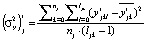 , где
, где 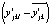 – отклонение экспериментальных значений переменной
– отклонение экспериментальных значений переменной 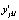 от их математических ожиданий
от их математических ожиданий 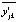 в каждой точке факторного пространства, индексы j и k нумеруют каждое из ljk измерений в каждой из nj точек факторного пространства.
в каждой точке факторного пространства, индексы j и k нумеруют каждое из ljk измерений в каждой из nj точек факторного пространства.
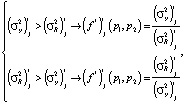 (9)
(9)
где в первом случае p1 – число степеней свободы в первом случае для остаточной дисперсии, во втором – для дисперсии воспроизводимости, p2 – число степеней свободы в первом случае для дисперсии воспроизводимости, во втором – для остаточной дисперсии. Гипотеза о равенстве дисперсий принимается в качестве нулевой гипотезы Н0 при альтернативной гипотезе Н1 о неравенстве дисперсии. Далее проверяем соотношение (10)
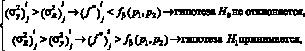 (10)
(10)
где fβ(p1; p2) – коэффициент Фишера на уровне значимости β с числами степеней свободы p1 для остаточной дисперсии в первом случае, а во втором – для дисперсии воспроизводимости, и p2 в первом случае для дисперсии воспроизводимости, а во втором – для остаточной дисперсии, соответственно.
Значимость коэффициентов регрессии i-й модели при температуре Tj проверяется с применением t-критерия Стьюдента. В качестве нулевой принимается гипотеза о равенстве нулю γ-го коэффициента регрессии (γ = 0, 1) и рассчитывается статистика
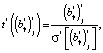 (11)
(11)
где 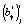 – точечная оценка γ-го коэффициента линейной регрессии, а
– точечная оценка γ-го коэффициента линейной регрессии, а 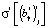 – точечная оценка стандартной ошибки для этого коэффициента. Расчетное значение статистики
– точечная оценка стандартной ошибки для этого коэффициента. Расчетное значение статистики 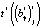 сравнивается с табличным значением tβ. Если
сравнивается с табличным значением tβ. Если
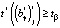 , (12)
, (12)
коэффициент считается значимым.
Модель имеет практическую ценность, если коэффициент корреляции 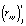 и показатель согласованности Стьюдента
и показатель согласованности Стьюдента 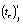 , вычисляемые по формулам
, вычисляемые по формулам
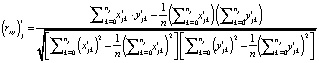
и 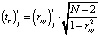 , соответственно, удовлетворяют неравенствам
, соответственно, удовлетворяют неравенствам
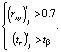 (13)
(13)
Результаты исследования и их обсуждение
Для экспериментального изучения были выбраны химические реакции в цепочке фторидной переработки золы ЗБТЭЦ с получением полезных компонентов. Объект исследования – электромагнитная фракция золы. Состав в мас. %: SiO2 – 54.27; Al2O3 – 21.01; Fe3O4 – 7.82; TiO2 – 0.66; CaO – 8.24; MnO – 0.30; MgO – 2.49; Na2O – 0.40; K2O – 1.23; P2O5 – 0.08; SO3 – 0.27; п.п.п. – 2.91.
Полезные компоненты извлекаются из золы фторидно-аммониевой переработкой в течение 0.5–4.5 часа при температурах 100–200 °С. В ходе реакции образуются следующие продукты: порошок спекшихся гек- сафторосиликата аммония ((NH4)2SiF6) и гек- сафтороалюмината аммония ((NH4)3AlF6), фторидов щелочных металлов (NaF и KF), флюорита (CaF2) и гематита (Fe2O3), а также летучих аммиака (NH3), фтороводорода (HF) и паров воды (H2O). Термической обработкой полученного спека в течение 1 часа при температурах 350–550 °С путем сублимации отделяется гексафторосиликат аммония ((NH4)2SiF6), далее в процессе его гидролизации аммиачной водой (NH4OH) образуется аморфный кремнезем (SiO2). Остальные компоненты извлекаются из порошкообразного спека в результате водной и кислотной обработки. Изучается химическая реакция спекания образца золы с ГДФА. В эксперименте измеряется убыль массы образца в последовательные отсчеты времени при каждой из исследуемых температур.
Кинетические кривые, интегральная и дифференциальная, исследуемой реакции спекания показаны на рис. 1. Из рис. 1а видно, что реакция при трех нижних температурах продолжается в течение всего эксперимента, причем при нижней температуре насыщение вообще отсутствует, а при второй и третьей, несмотря на то что наклон кривых к концу эксперимента сильно уменьшается, на плато они все равно не выходят до конца эксперимента. При верхней температуре степень превращения вещества достигает насыщения между 1,5 и 2 часами, т.е. в течение двух часов реакция прекращается. Такое различие между временами протекания реакции при различных температурах очевидно из соотношения значений констант скоростей в табл. 1 (приблизительно 1: 5: 8: 22). Скорость реакции при верхней температуре в 22 раза выше, чем при нижней температуре. На рис. 1б изображены дифференциальные кинетические кривые изучаемой реакции спекания. Из рис. 1б видно, что дифференциальные кривые 2, 3 и 4 начинаются с высоких значений скоростей реакции и быстро (в течение часа) спадают почти на порядок величины. Высокие значения скоростей реакции связаны с большими количествами контактирующих частиц реагентов в начале реакции. По мере израсходования атомов реагентов скорость реакции уменьшается (рис. 1б), однако степень превращения вещества нарастает (рис. 1а) из-за увеличения площади реакционной зоны [8]. Тем не менее примерно через 0.5 часа, скорость реакции уменьшается на порядок величины: кривые 2, 3 и 4 на рис. 1а переходят в режим насыщения (и выходят на плато, как кривая 4, через 2 часа после начала реакции) или близкий к насыщению (сильно уменьшают наклон, как кривые 2 и 3). На рис. 1б к этому моменту (2 часа) кривая 4 обращается в 0, а кривые 2 и 3 сохраняют небольшие, но неравные нулю значения до конца реакции. Реакция при 2-й и 3-й температурах с небольшой скоростью продолжается, и поэтому кривые 2 и 3 на рис. 1а не выходят на плато до конца реакции. Отметим, что в течение 1 часа реакция при этих температурах, по-видимому, протекает за счет химического взаимодействия между частицами, скорость которого постепенно убывает из-за уменьшения концентрации частиц. Уменьшение концентрации частиц приводит к увеличению среднего расстояния между ними, поэтому через 1 час после начала реакции существенное значение приобретает диффузия частиц через обедненные частицами области. Небольшое значение скорости реакции при нижней температуре по сравнению со скоростями реакций при других температурах говорит о том, что вся реакция протекает в зоне диффузии при этой температуре, что подтверждается значением энергии активации в табл. 1 (строка 5, столбец 2).
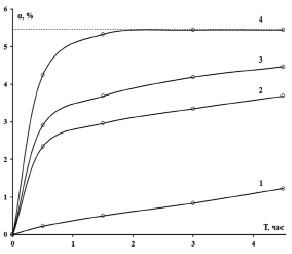
а)
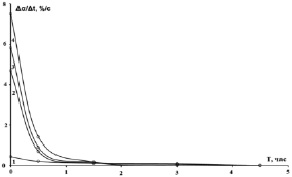
б)
Рис. 1. Графики экспериментальных кривых для реакции спекания образца золы с ГДФА: a) интегральная кинетическая кривая α(t); б) дифференциальная кинетическая кривая ∆α(t)/∆t при температурах: 1 – 50 °C, 2 – 100 °C, 3 – 150 °C, 4 – 200 °C
Таблица 1
Предварительные кинетические характеристики (кинетические характеристики, полученные в результате предварительного отбора по величине погрешностей аппроксимаций) для реакции спекания золы ЗБТЭЦ с ГДФА
|
№ |
1 |
2 |
3 |
4 |
5 |
|
1 |
Tj, °С |
50 |
100 |
150 |
200 |
|
2 |
|
0.000804 |
0.003733 |
0.006622 |
0.017998 |
|
3 |
|
0.76 |
0.25 |
0.39 |
0.48 |
|
4 |
|
3 |
3 |
2 |
2 |
|
5 |
Ei |
13 |
24 |
||
|
6 |
|
Степ |
ЕА |
||
|
7 |
ЗР |
Диффузионная |
Переходная |
||
|
8 |
fij(t) |
|
|
|
|
Примечания: в строке 2 размерность констант скоростей мин-1, сокращения ЗР – зона реакции, Степ – Степенной закон, ЕА – уравнение Ерофеева-Авраами.
Математической обработкой экспериментальных результатов рассчитываются кинетические характеристики реакции спекания и помещаются в табл. 1.
Оценки коэффициентов линейной регрессии 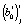 и
и 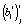 для i-й модели при j-й температуре рассчитываются по уравнению (4), а по ним кинетические параметры реакции
для i-й модели при j-й температуре рассчитываются по уравнению (4), а по ним кинетические параметры реакции 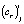 и
и 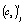 (строки 2 и 3 в табл. 1) для каждой температуры Tj (строка 1 в той же таблице) и каждой модели (формулы (1)–(3) и (4)).
(строки 2 и 3 в табл. 1) для каждой температуры Tj (строка 1 в той же таблице) и каждой модели (формулы (1)–(3) и (4)).
Уравнение реакции для i-й модели и j-й температуры 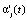 (строка 6) определялось параметрической функцией с минимальной погрешностью аппроксимации
(строка 6) определялось параметрической функцией с минимальной погрешностью аппроксимации 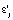 (строка 4). Для выбранного i0-го уравнения реакции при температуре
(строка 4). Для выбранного i0-го уравнения реакции при температуре 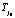 с его кинетическими параметрами
с его кинетическими параметрами 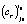 и
и 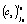 рассчитывалась энергия активации
рассчитывалась энергия активации 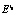 для i0-го уравнения реакции (строка 5) по формуле (5). По величине этой энергии активации для каждой температуры определялась зона реакции (строка 7). Выбранные параметрические функции (формулы (1)–(3)) с параметрами
для i0-го уравнения реакции (строка 5) по формуле (5). По величине этой энергии активации для каждой температуры определялась зона реакции (строка 7). Выбранные параметрические функции (формулы (1)–(3)) с параметрами 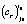 и
и 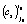 из строк 2 и 3 для каждой температуры представляют собой функции отклика
из строк 2 и 3 для каждой температуры представляют собой функции отклика 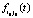 для данной температуры (строка 8), изображенные на рис. 2а.
для данной температуры (строка 8), изображенные на рис. 2а.
Как видно из табл. 1, по предварительным результатам отбора реакция фторирования образца золы ГДФА протекает при температуре 50 °С по степенному закону с энергией активации 13 кДж/моль и при температурах 100, 150 и 200 °С по уравнению Ерофеева-Авраами с энергией активации 24 кДж/моль. По величине энергии активации определяем зоны реакции при каждой температуре: при нижней температуре 13 кДж/моль < 20 кДж/моль, следовательно, зона диффузионная, а при верхних температурах значение энергии активации 24 кДж/моль попадает в интервал 20 кДж/моль < 24 кДж/моль < 50 кДж/моль, следовательно, зона переходная [9; 10].
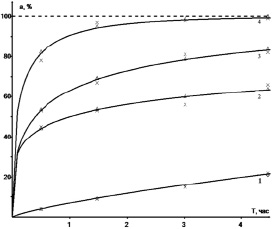
а)
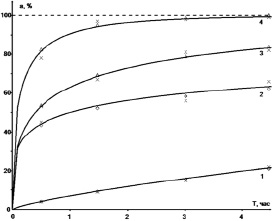
б)
Рис. 2. Графики расчетных функций отклика для реакции спекания образца золы с ГДФА: а) предварительные и б) окончательные. Температуры: 1 – 50 °C, 2 – 100 °C, 3 – 150 °C, 4 – 200 °C. Треугольниками обозначены кривые, рассчитанные по уравнению Ерофеева-Авраами, а ромбиками – по степенному закону
На рис. 2а изображены предварительные расчетные функции отклика для данной реакции при каждой исследуемой температуре, которая показывает неплохое соответствие между экспериментальными значениями (крестики) и теоретическими значениями (для степенного закона ромбики, для уравнения Ерофеева-Авраами – треугольники).
Проверка достоверности полученных предварительных результатов расчета кинетических характеристик осуществляется при помощи ряда статистических гипотез, имеющих вспомогательный характер и описанных выше. Предварительные статистические характеристики, которые рассчитываются, исходя из предварительных кинетических характеристик по формулам (8)–(14), и используются для проверки статистических гипотез для каждой температуры, сведены в табл. 2.
Таблица 2
Предварительные статистические характеристики (статистические характеристики, полученные в результате предварительного отбора по величине погрешностей аппроксимаций) и их значения для реакции фторирования ГДФА золы ЗБТЭЦ
|
№ |
1 |
2 |
3 |
4 |
5 |
|
1 |
Температура (Tj), °С |
50 |
100 |
150 |
200 |
|
2 |
Уравнение протекания реакции (αjk(t)) |
Степ |
ЕА |
||
|
3 |
Статистика Фишера для однородности дисперсии (f*(h1; h2)) |
4.74 |
6,72 |
6,17 |
14,49 |
|
4 |
Коэффициент Фишера для однородности дисперсии (fβ(h1; h2)) |
19,37 |
19,37 |
||
|
5 |
Статистика Фишера для адекватности регрессии (f*(p1; p2)) |
2.0 |
2,66 |
3,38 |
4,1 |
|
6 |
Коэффициент Фишера для адекватности регрессии (fβ(p1; p2)) |
4,46 |
4,46 |
||
|
7 |
Статистика для свободного члена (t*(b0ij*)) |
94,28 |
0,25 |
21,87 |
25,06 |
|
8 |
Статистика для углового коэффициента (t*(b1ij*)) |
39,19 |
6,58 |
12,19 |
6,29 |
|
9 |
Коэффициент корреляции (rxy) |
1 |
0,96 |
0,99 |
0,95 |
|
10 |
Показатель согласованности Стьюдента (tr) |
27.71 |
4,65 |
8,62 |
4,45 |
|
11 |
Коэффициент Стьюдента (tβ) |
4,3 |
4,3 |
||
Примечание: коэффициенты Стьюдента и Фишера приводятся в соответствии с [11] и [12].
Сравнением статистик Фишера для однородности дисперсии из 3-й строки табл. 2 с соответствующим коэффициентом Фишера для гипотезы об однородности дисперсии (строка 4 в той же таблице) по формуле (8) подтверждаем однородность дисперсии воспроизводимости.
Адекватность линейной регрессионной модели следует из справедливости формулы (10), в которой статистики Фишера для адекватности регрессии из 5-й строки меньше, чем соответствующие коэффициенты Фишера из 6-й строки. Значения коэффициента корреляции в 9-й строке по формуле (13) означают высокую степень связи между входными и выходными данными и, соответственно, практическую ценность функции отклика. Статистическую значимость коэффициента корреляции подтверждают значения показателя согласованности Стьюдента из 10-й строки, большие коэффициента Стьюдента из 11-й строки (формула (13)).
Значимость коэффициентов регрессии вытекает из того, что статистики, как для свободного члена из 7-й строки, так и для углового коэффициента из 8-й строки, больше, чем коэффициент Стьюдента в 11-й строке (формула (12)). Исключением является вторая температура (столбец 3), при которой соответствующая статистика 0.25 (в строке 8) меньше коэффициента Стьюдента 4.3 (в строке 11), что означает справедливость нулевой гипотезы о равенстве нулю данного коэффициента. Положение может исправить использование конкурирующего с уравнением Ерофеева-Авраами для этой температуры степенного закона, который дает чуть большую погрешность аппроксимации (4 % вместо 3 %), но статистически значимый свободный член при данной температуре (статистика 25.36 в 7 столбце в табл. 4). В итоге результаты предварительного расчета, проведенного по величине погрешности аппроксимации, должны быть пересмотрены. Реакцию при температуре 100 °С мы будем считать протекающей по степенному закону и, следовательно, должны заменить кинетические и статистические характеристики реакции спекания при температуре 100 °С в табл. 1 и 2, рассчитанные для уравнения Ерофеев-Авраами, на аналогичные характеристики для степенного закона и поместить их в табл. 3 и 4.
Таблица 3
Окончательные кинетические характеристики (кинетические характеристики, полученные после статистической проверки пяти гипотез регрессионного анализа) для реакции фторирования ГДФА золы ЗБТЭЦ для температуры 100 °С
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
Закон |
k01 |
m01 |
ε01 |
E0 |
Зона реакции |
f01(t) |
|
2 |
α01(t) |
0,002356 |
0.16 |
4 |
13 |
Диффузионная |
|
Примечание: в строках 1 и 2 табл. 3 приведены обозначения величин и их значения, соответственно, для величин из столбца 1 табл. 1.
Таблица 4
Результаты статистической проверки гипотез регрессионного анализа
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
αik(t) |
(f*(h1; h2)) |
(fβ(h1; h2)) |
(f*(p1; p2)) |
(fβ(p1; p2)) |
|
|
rxy |
tr |
tβ |
|
2 |
Степ |
4,21 |
19,37 |
3,59 |
4,46 |
25.36 |
7.66 |
0.97 |
5.42 |
4.3 |
|
3 |
i = 0, j = 1. |
Дисперсия однородна (8) |
Модель адекватна (10) |
Коэффициенты значимы (12) |
f01(t) практически ценна (13) |
|
β = 0.05 |
|||
Примечание: в строках 1, 2 и 3 табл. 4 приведены величины, их значения и результаты проверки гипотез, соответственно, для столбца 1 табл. 2. В 3 строке в столбцах с (2) по (9) в скобках приведены номера формул, по которым вынесено заключение о проверке гипотезы.
В табл. 3 показаны кинетические характеристики реакции спекания исследуемого образца с ГДФА при температуре 100 °С при пересчете их в соответствии со степенным законом. Закон протекания символически изображен при помощи зависимости степени превращения вещества от температуры αij(t), в которой индексы i и j принимают значения 0 и 1 для степенного закона и температуры 100 °С, соответственно. Таким образом, имеем α01(t) в столбце 1 второй строки табл. 3. Значения остальных кинетических характеристик – в других столбцах второй строки этой таблицы.
Из строки 3 табл. 4 видно, что все гипотезы регрессионного и корреляционного анализа, которые проверяются в работе, выполняются для новой (степенной) регрессионной модели при температуре 100 °С, а также указаны формулы, по которым эта проверка осуществляется.
На рис. 2а, как отмечалось выше, показаны функции отклика, найденные по результатам отбора по величине погрешностей аппроксимации, а на рис. 2б – после статистической проверки. Отличие заключается в кривой 2, показанной на рис. 2а треугольниками, а на рис. 2б ромбиками: кривая на рис. 2а отклоняется сильнее от эксперимента в точке 2 часа, а кривая на рис. 2б в точке 4,5 часа. Расхождения в других точках незначительны. Расхождения возникают потому, что погрешность аппроксимации отражает отклонения от эксперимента функции отклика (формулы 5), которая является нелинейной регрессией и строится в естественных координатах, а статистические характеристики вычисляются для линейной регрессии (формула (4)), которая строится в обобщенных координатах.
Заключение
В данной работе проводится расчет кинетики спекания образца золы ЗБТЭЦ с ГДФА. Топохимические расчеты выполняются по созданной нами программе на языке Visual Basic. В ходе расчетов апробируется программа и усовершенствуется методика расчета, включая статистическую проверку гипотез регрессионного и корреляционного анализов. Статистическая проверка гипотез регрессионного анализа проводится после предварительного выбора модели регрессии и последующего расчета кинетических характеристик реакции с целью выяснения вопроса о достоверности результатов расчета.
Так, при температуре 100 °С предварительно отбирается уравнение Ерофеева-Авраами, однако модель оказывается неадекватной по результатам статистической проверки гипотезы о значимости коэффициентов регрессии. При температуре 100 °С степенной закон имеет немного большую, чем уравнение Ерофеева-Авраами, погрешность аппроксимации (4 % вместо 3 %), но все рассчитываемые для него статистические величины проходят проверку. Поэтому окончательно считаем, что изучаемая реакция протекает при двух нижних температурах по степенному закону, а при двух верхних – по уравнению Ерофеева-Авраами и имеет кинетические характеристики, указанные в табл. 1 и 3 для температур 50, 150, 200 °С и температуры 100 °С, соответственно.




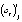
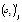
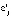
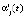
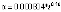
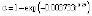
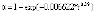
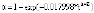
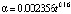
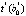
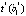
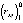 значим (13)
значим (13)