Рыночная структура олигополии характеризуется наличием небольшого числа фирм-конкурентов, которые выстраивают свою экономическую политику исходя из действий своих конкурентов. Отличительной чертой олигополии является факт обязательной ответной реакции на любые действия конкурентов [1, с. 27].
В данной работе рассматривается динамическая программная реализация следующих моделей олигополистической конкуренции: модель Курно, модель Штакельберга и модель картельного сговора.
В модели Курно каждая фирма выбирает оптимальный объём производства на основании информации об объёме выпуска конкурента и рыночной ситуации. Модификацией модели Курно является модель Штакельберга, согласно которой можно выделить фирму лидера (придерживается стратегии монополиста) и последователя, или ведомого (действует согласно модели Курно). Другим вариантом взаимодействия является сговор фирм, которые совместно устанавливают некоторые соглашения по распределению рынка. Такая ситуация соответствует модели картельного сговора [2].
Существующие компьютерные модели Коршунова (Duopoly 1–3) [3, 4], реализующие количественную дуополию, основаны на биматричной игре с чистыми стратегиями. Программная реализация включает в себя программное окно для задания параметров и программное окно для графической интерпретации результата при помощи кривых реакции.
Целью работы является разработка компьютерной модели на основе дифференциальных уравнений, которая реализует три математические модели количественной олигополистической конкуренции: модель Курно, модель Штакельберга и модель картельного сговора.
Материалы и методы исследования
Функция отраслевого спроса задаётся следующим образом.
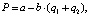
где P – цена продукции, a, b – коэффициенты функции спроса,
q1 – объём выпуска фирмы 1, q2 – объём выпуска фирмы 2.
Задача каждой фирмы – максимизация прибыли. Из этого факта получаем следующее.
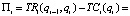
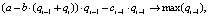
где Пi – прибыль i-й фирмы, TRi – выручка i-й фирмы, TCi – общие издержки,
ci – издержки i-й фирмы.
Модели Курно в непрерывном времени соответствует уравнение [5, с. 5–6].
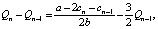
Q(t) – объём производства.
Этому конечно-разностному соответствует следующее дифференциальное уравнение
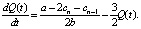
Решение этого дифференциального уравнения:
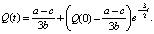 (1)
(1)
Модели Штакельберга в непрерывном времени для фирмы лидера [3] соответствует следующее дифференциальное уравнение:
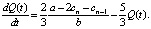
Решение данного уравнения:
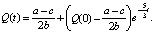 (2)
(2)
Модели Штакельберга в непрерывном времени для фирмы последователя [3] соответствует следующее дифференциальное уравнение:
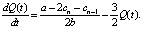
Решение данного уравнения:
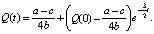 (3)
(3)
Модели картельного сговора [6] в непрерывном времени соответствует следующее дифференциальное уравнение:
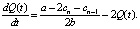
Решение дифференциального уравнения:
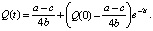 (4)
(4)
Модели картельного сговора, если одна из фирм решает нарушить картельный сговор [6] в непрерывном времени соответствует следующее дифференциальное уравнение:
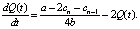
Решение данного уравнения:
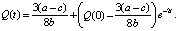 (5)
(5)
Решения (1)–(5) дифференциальных уравнений для моделей Штакельберга и картельного сговора получены в [5] аналогично модели Курно.
Предлагаемая компьютерная модель, основанная на визуализации решений дифференциальных уравнений (1)–(5), позволяет динамически задавать параметры рынка (функцию спроса) и характеристики предприятий (функцию издержек и/или объём выпуска), на основании данной информации пользователь может получать следующую информацию.
1. Определение равновесного объёма выпуска фирм при различных моделях (модель Курно, модель Штакельберга и модель картельного сговора) олигополистической конкуренции.
2. Определение цены продукции на рынке и прибыли фирм при равновесном или определённо заданном объёме производства.
3. Определение целесообразности текущего объёма выпуска в сравнении с равновесным выпуском представленных моделей и получение рекомендации по его изменению.
4. Результаты сравнительного анализа показателей (выпуск, цена и прибыль) у различных моделей.
Результаты исследования и их обсуждение
Для достижения поставленной цели была разработана компьютерная модель [7] с использованием языка программирования C#, в которой реализовано пять программных окон. На рис. 1 представлено главное программное окно.
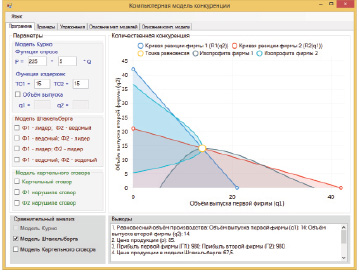
Рис. 1. Главное окно программы – модель Курно, общий случай
Главное программное окно (рис. 1) можно разделить на 4 части:
1) Параметры модели. В данной части задаются основные параметры компьютерной модели: функция спроса, функции издержек, объём выпуска, а также выбирается стратегия поведения. Всего можно выделить 9 различных стратегий.
- модель Курно – общий случай (выбрана по умолчанию);
- модель Курно – частный случай с заданным объёмом производства;
- модель Штакельберга – Фирма 1 – лидер, Фирма 2 – последователь;
- модель Штакельберга – Фирма 1 – последователь, Фирма 2 – лидер;
- модель Штакельберга – Фирма 1 – лидер, Фирма 2 – лидер;
- модель Штакельберга – Фирма 1 – последователь, Фирма 2 – последователь;
- модель Картельного сговора – общий случай;
- модель Картельного сговора – Фирма 1 нарушила сговор;
- модель Картельного сговора – Фирма 2 нарушила сговор.
2) График. В данной области производится графическая визуализация результатов. На графике строятся кривые реакции и изопрофиты для двух фирм, а также отмечается точка равновесия.
3) Выбор модели для сравнительного анализа. В данной области производится выбор между моделями Курно, Штакельберга и Картельного сговора для сравнительного анализа со стратегией, выбранной в первой области (области задания параметров компьютерной модели).
4) Область с результатами работы программы. В данной области представлены выводы из расчёта по выбранным параметрам, включая сравнительный анализ.
Для демонстрации особенностей работы программы представлены следующие примеры на рис. 2–4.
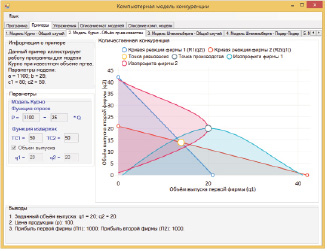
Рис. 2. Модель Курно – Объём производства известен
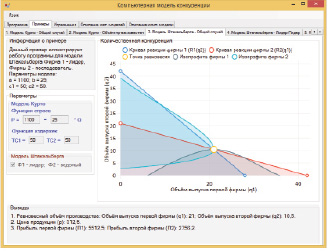
Рис. 3. Модель Штакельберга – Общий случай (Ф1 – лидер; Ф2 – ведомый)
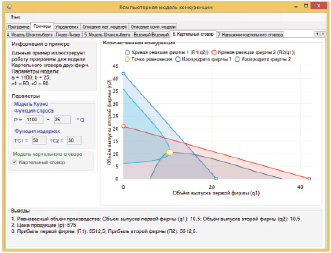
Рис. 4. Модель картельного сговора – Общий случай
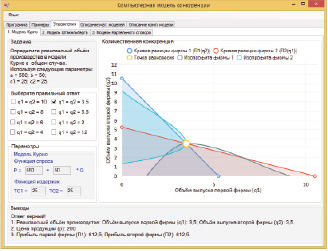
Рис. 5. Программное окно упражнения – Модель Курно
В модели кроме примеров реализованы упражнения на модель Курно (рис. 5), Штакельберга и картельного сговора. В качестве задания в этих упражнениях необходимо найти равновесный объём производства двух фирм и выбрать верный вариант из предложенных вариантов. Если выбран правильный вариант, то на графике отобразится точка равновесия, в выводах будет отражено, что пример выполнен верно. В противном случае система сообщит, что выбран неправильный ответ.
Заключение
Разработанная компьютерная модель реализует основные математические модели количественной олигополистической конкуренции и может использоваться для процесса анализа олигополистического рынка при принятии управленческих решений, а также для изучения различных механизмов взаимодействия в олигополистической конкуренции. Для успешного освоения компьютерной модели представлены примеры, которые демонстрируют функциональность системы. Наряду с примерами предлагаются упражнения.



