Исследование колебаний в кольцевых областях является достаточно сложной задачей теории нелинейных колебаний [1]. В статье рассматривается принцип переключения автоколебательных режимов, основанный на синтезе инвариантных многообразий [2]. Инвариантность многообразия означает, что траектории, начинающиеся на этом многообразии, остаются на нем при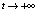 
. Если многообразие гладкой системы – замкнутое и компактное, то траектории системы неограниченно продолжаемы на нем [3]. Из существования и единственности решения задачи Коши следует, что траектории системы, начинающиеся вне инвариантного многообразия, не могут его пересекать при 
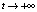. Следовательно, если многообразие является границей некоторой области, то траектории системы, начинающиеся внутри этой области, будут оставаться в ней при 
.
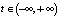Автоколебания являются следствием собственных внутренних свойств системы. При этом амплитуда и частота колебаний не будут зависеть от начальных условий процесса. Автоколебания возникают только при наличии нелинейности. Возбуждение автоколебательного режима означает формирование устойчивого предельного цикла в пространстве состояний системы.
С изменением некоторых основных параметров нелинейной системы могут происходить бифуркации, вызывающие перестройку фазовых траекторий.
В статье [4] исследован механизм бифуркации на примере ритмов Ламэ. Одной из прикладных задач динамики биологических ритмов является управление геометрией профиля ритма, что, в частности, связано с управлением амплитудами процессов Ламэ [2]. Типовая классификация ритмов определяется связной системой осцилляторов с определенным типом доминирующей нелинейности. Рассматривается задача построения многосвязной системы, передача управляемых сигналов в которой осуществляется по 2n-каналам. Решение задачи приводит к определению слоев, ограниченных замкнутыми инвариантными многообразиями.
В результате бифуркации ритм Ламэ переключается с одного автоколебательного режима на другой. Это соответствует изменению свойства устойчивости предельных циклов.
В работе [5] получена зависимость между отношением площадей областей, ограниченных предельными циклами соответствующих подсистем, и амплитудами управляемой системы.
В данной работе в структуру управляющих функций вводятся нелинейности более высокого порядка. Это позволяет существенно увеличить гибкость управления с целью изменения размеров области, ограниченной устойчивым предельным циклом, в отношении регулирования характеристик установившегося колебательного процесса.
Постановка задачи
Рассмотрим вложенные в R2n гладкие многообразия: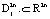 
, взаимное расположение которых в пространстве определим как
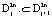, (1)
где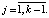 
Границы областей 
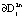зададим уравнениями
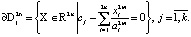
Для выполнения условия (1) достаточно, чтобы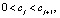 
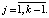Нижняя и верхняя границы каждой кольцевой области являются нечетно-мерными многообразиями, гомеоморфными сферам.
Рассмотрим задачу синтеза автоколебаний на слое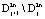 
, 
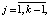при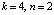 
:
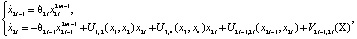
где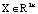 
– вектор состояния пространства системы управления; 
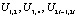– внутренние функции управления; 
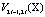– обменные функции управления, 
.
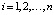Решение задачи стабилизации колебаний на слое сводится к получению условий инвариантности, асимптотической устойчивости верхней или нижней границы кольцевой области в фазовом пространстве системы [6]. При m = 1 управлять размерами областей можно с помощью регулирования соответствующих амплитуд колебательных подсистем. При m > 1 в качестве управляющих параметров во многих задачах следует рассматривать соотношения площадей внутренних областей, ограниченных инвариантными кривыми.
Параметры управления и стабилизация колебаний в кольце
Структуру управлений определим следующим образом:
1) внутрисистемное управление первой подсистемы
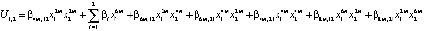
2) внутрисистемное управление второй подсистемы
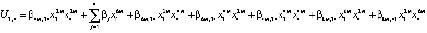
3) внутрисистемное управление i-той подсистемы, i = 1, 2
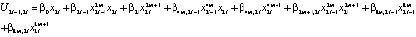
4) межсистемное управление
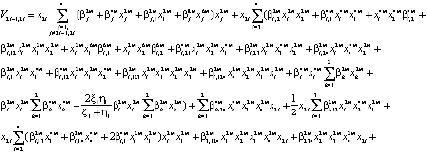
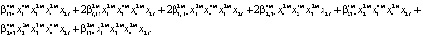
Рассмотрим функцию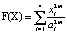 
. Данная функция знакопостоянна, как на множестве, примыкающем к ее поверхности уровня изнутри, так и в некотором δ-слое, прилегающем к границе извне. Запишем условия инвариантности для границ слоя:
.
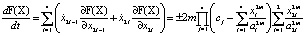Равенство выполняется тогда и только тогда, когда вектор X принадлежит поверхности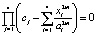 
. Условие инвариантности будет выполняться только для одной из поверхностей уровня функции F(X). Выполним подстановку и необходимые преобразования. Условия на параметры управлений примут вид:
- для внутрисистемного управления первой подсистемы
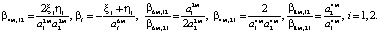
- для внутрисистемного управления второй подсистемы
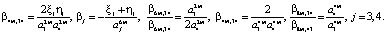
- для внутрисистемного управления i-той подсистемы, i = 1, 2
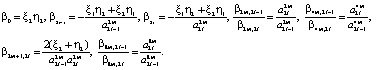
- для межсистемного управления
,
,
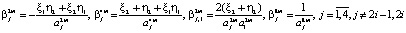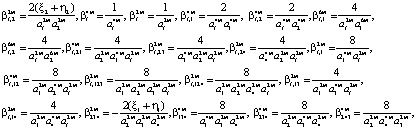
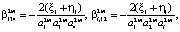
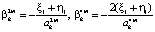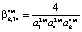при условии, что 
,
.
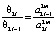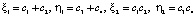При этих параметрах управляющих функций границы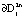 
, j = 4, кольцевой области инвариантны для траекторий, с начальными условиями, определенными на множествах
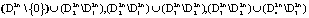
и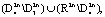 
соответственно.
Стабилизирующие управления с требуемыми свойствами могут быть реализованы в нескольких случаях, связанных между собой переключением автоколебательных режимов с помощью смены знака перед параметрами управления [4].
Исследуем поведение системы (2) на следующих областях:
, 
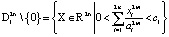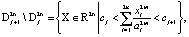
где j = 1, 2, 3,
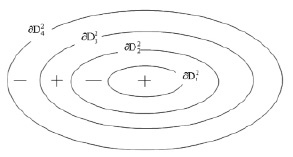
Рис. 1. Знакоопределенность полной производной функции F(X)
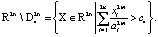
1. Для траекторий системы, начинающихся внутри области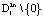 
, полная производная будет определенно положительной в области 
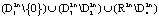и определенно отрицательной на множестве 
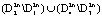(рис. 1). Следовательно, траектории системы, начинающиеся внутри множества 
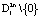, притягиваются к границе 
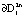. В силу инвариантности поверхности 
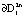далее траектории ее не пересекают, оставаясь внутри области, ограниченной 
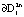. Траектории скручиваются от границы 
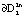к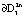 
и вовнутрь слоя с притяжением к границе 
.
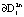Траектории системы, начинающиеся внутри множества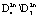 
, притягиваются к границе 
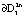и скручиваются от границы 
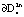в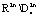 
.
2. Определим поведение полной производной функции на движения системы (2) после изменения знака перед коэффициентами функций управления. В этом случае полная производная будет отрицательной на множестве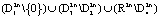 
и положительной в области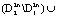 
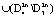. Таким образом, траектории системы, начинающиеся внутри множества 
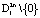, стягиваются в начало координат. Траектории системы, начинающиеся внутри множества 
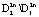, притягиваются к границе 
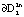и скручиваются от границы 
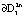в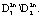 
Траектории системы, начинающиеся внутри множества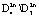 
, скручиваются от границы 
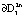и притягиваются к границе 
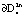в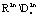 
.
Во внутренней и внешней δ – окрестности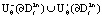 
поверхности 
, 
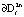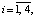нет ω и α – предельных точек, как и на самой поверхности, нет α – предельных точек. Согласно теореме В.И. Зубова об асимптотической устойчивости инвариантных множеств с учетом описанного поведения траекторий можно сделать вывод, что множество 
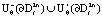является областью притяжения для 
.
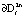Численное моделирование. Переключение режимов автоколебаний
Геометрически в R2 слой определяют концентрически расположенные предельные циклы. Внутренним предельным циклом является граница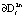 
, внешним – 
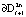, i = 1, 2, 3. В одном случае интегральные трубки описывают выход на режим устойчивых автоколебаний с параметрами предельных циклов 
, 
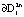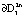, в другом случае – с параметрами циклов 
, 
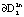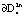. На рис. 2 интегральная кривая скручивается с трубки внешнего предельного цикла 
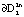к трубке внутреннего предельного цикла 
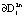. На рис. 3 наблюдается переключение режимов автоколебаний, в результате которого внутренний предельный цикл 
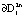становится неустойчивым. Интегральная кривая скручивается от границы 
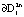и притягивается к поверхности 
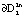. Внешний предельный цикл 
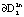приобретет устойчивость (рис. 4).
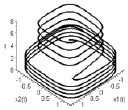
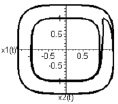
Рис. 2. Устойчивая внутренняя граница слоя
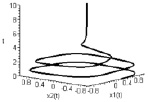
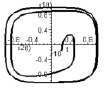
Рис. 3. Потеря устойчивости внутренней границей слоя
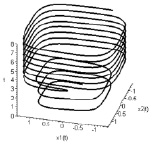
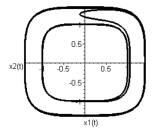
Рис. 4. Устойчивая внешняя граница слоя
Заключение
Полученные в работе системы управления со стабилизацией на слое могут быть использованы в задачах биомедицинских технологий, при решении задач управляемого движения шагающих машин. Принцип переключения между устойчивыми режимами позволит варьировать размеры области стабилизации, определять характеристики колебаний.