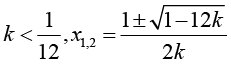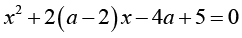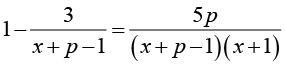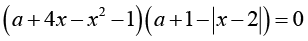Введение
Быстро меняющаяся реальность требует сегодня от человека развитых навыков критического и творческого мышления для решения нестандартных задач. В ответ на это главной целью образования становится формирование гибкой и самостоятельной личности. Такой человек должен уметь быстро находить информацию, анализировать ее, на основе этого анализа создавать новые знания и предлагать уникальные решения. Современному обществу нужны люди с исследовательской жилкой, способные к постоянному познанию и инновациям, то есть способные осуществлять исследовательскую деятельность.
Федеральный государственный образовательный стандарт (ФГОС) среднего общего образования закрепляет концепцию «портрета выпускника школы», определяющую ключевые личностные характеристики, необходимые для успешной интеграции в общество. В рамках этого идеала обучающийся не только должен владеть фундаментальными научными методами познания, но и быть мотивированным к реализации творческого, исследовательского и проектного потенциала, в том числе в инновационной сфере. Особый акцент делается на гражданском самоопределении: выпускник призван уважать, сохранять и транслировать далее культурное наследие и духовные ориентиры России. Реализация этих требований напрямую зависит от сформированности критического мышления, способности к анализу и верификации информации, выдвижению и проверке гипотез, а также формулированию обоснованных выводов. Значимо, что данный комплекс умений составляет ядро как исследовательской деятельности в целом, так и процесса решения нестандартных математических задач, в частности. Таким образом, центральными проблемами современного математического образования становятся задачи целенаправленного развития исследовательских умений и обучения решению нестандартных задач.
Методический аспект формирования исследовательских умений в ходе изучения математики рассматривался в работах современных методистов-математиков. Большинство из них подчеркивали важность формирования исследовательских умений для осуществления учебно-исследовательской деятельности и выделяли теоретические аспекты проблемы формирования исследовательских умений, такие как структура исследовательской деятельности, классификация исследовательских умений, способы их формирования [1]. Однако в методике обучения математике отсутствуют модели формирования исследовательских умений, нет четко сформулированных рекомендаций для учителей по формированию и оценке исследовательских умений с целью решения математических задач.
Понятие учебно-исследовательской деятельности в методической литературе трактуется аналогично [2–4]. Так, В.А. Далингер отмечает одну из основных черт учебно-исследовательской деятельности – творческий характер, поскольку она реализуется обучающимися с преимущественно самостоятельным применением научных методов познания [5]. Он трактует учебно-исследовательскую деятельность как самостоятельное решение учебной проблемы, которое включает в себя поиск необходимой информации, а также прогнозирование итогов работы и планирование шагов для их достижения [6]. Такое определение отражает компоненты исследовательской деятельности, аналогичные этапам решения нестандартных математических задач.
Подробная структура учебно-исследовательской деятельности в условиях инновационного образования и развития методической науки рассмотрена в работах А.М. Жанбурбаевой [7] и Н.Л. Стефановой [4]. С позиции метаметодического подхода профессор Н.Л. Стефанова выделяет следующие структурные компоненты учебно-исследовательской деятельности: 1) идентификация и формулирование исследовательской проблемы; 2) систематизация и обработка эмпирических данных; 3) построение исследовательской гипотезы; 4) проведение экспериментальной проверки и теоретического подтверждения выдвинутой гипотезы; 5) интерпретация полученных результатов и формулирование выводов.
Данные этапы в контексте решения нестандартных математических задач можно сформулировать следующим образом: 1) анализ содержания и определение типа задачи, формулирование требования; 2) установление теоретического базиса задачи и проверка его на частных случаях (если это необходимо); 3) построение последовательности предполагаемых действий, определяющих способ решения; 4) теоретическое обоснование выполняемых действий и подтверждение выбранного способа решения; 5) интерпретация полученных результатов и формулирование выводов. Назовем эти этапы ключевыми этапами учебно-исследовательской деятельности в процессе решения нестандартных математических задач.
Для эффективной реализации исследовательской деятельности в школьном математическом образовании обучающиеся должны владеть исследовательскими умениями. В научно-методической литературе существуют разные определения этого понятия. Одни (О.Л. Калинина, А.Ю. Фадеева, В.А. Гусев) определяют исследовательские умения перечислением действий, входящих в их состав. Другие (О.В. Аксенова, М.А. Якунчев, И.Ф. Маркинов, Н.Г. Семенова, Д.А. Кириллова, О.Н. Белова) формулируют определение исследовательских умений через ближайший род и видовые отличия, не касаясь подробно действий, которые необходимо освоить [8; 9, с. 105].
Опираясь на анализ существующих определений, в контексте обучения решению нестандартных задач под исследовательскими умениями обучающихся будем понимать комплекс умений, обеспечивающих самостоятельную полную или частичную реализацию ключевых этапов учебно-исследовательской деятельности. Данные умения активизируются в ситуациях решения нестандартных задач и предполагают активное применение методов научного познания.
Будем рассматривать общие и специальные исследовательские умения. К общим исследовательским умениям относятся: умение видеть проблему, ставить гипотезы, находить и анализировать информацию, проводить эксперименты, делать выводы и умозаключения, то есть те умения, которые необходимы для проведения любого исследования, независимо от содержания. Специальные исследовательские умения – это умения, которые формируются и используются в конкретной предметной области, например в математике.
Под нестандартной задачей по математике будем понимать задачу, решение которой невозможно по уже известному алгоритму или правилу, а требует применения исследовательских умений, творческого поиска, суть которого заключается в активном нахождении новых, нестандартных и оригинальных идей, подходов и решений, которые отличаются от уже существующих.
Как показывает практика, навык решения нестандартных задач по математике зависит от уровня сформированности исследовательских умений школьников. Создать уникальный алгоритм решения задачи – это значит провести исследование проблемы, содержащейся в ней: выделить вопрос, выдвинуть гипотезу, обосновать ее, построить путь ее доказательства и проверить результат. Все эти этапы можно отождествить с этапами решения нестандартной математической задачи.
Этапы формирования исследовательских умений выделены в ряде работ. Остановимся на этапах, выделенных О.В. Аксеновой [10, c. 6] и В.Ю. Бодряковым [11]. Они рассматривают четыре этапа формирования исследовательских умений студентов: проблемно-поисковый, эвристический, диагностический, практический – и предлагают использовать лабораторные работы по математике на двух представленных этапах. Эти этапы можно адаптировать и к школьному образованию.
Многие методисты [12–14] предлагали для формирования исследовательских умений лишь отдельные, хотя и эффективные, с их точки зрения, типы задач. Такие задачи носят познавательный, исследовательский характер [15; 16]. При наличии многочисленных исследований современная дидактическая практика не обладает четко разработанной системой рекомендаций для учителей по поэтапному развитию данных умений в процессе обучения математике и их использованию в качестве инструмента решения нестандартных математических задач. Однако исследовательские умения составляют фундамент решения нестандартных задач по математике. В качестве таких задач выступают исследовательские задачи с параметром, задачи на поиск доказательства, задачи с множественным решением, геометрические задачи на построение, олимпиадные задачи и т. п.
Для разработки методики обучения решению нестандартных задач по математике авторами проведена диагностика уровня сформированности исследовательских умений обучающихся 10-го класса, основанная на решении нестандартных математических задач. Участниками эксперимента стали обучающиеся классов 10А и 10Б МОУ «Лицей № 4» г. о. Саранск Республики Мордовия, 42 чел.
Цель исследования – определить уровень сформированности исследовательских умений старшеклассников, проявляемых при решении нестандартных математических задач.
Необходимо было проверить: 1) владение общими исследовательскими умениями, реализуемыми в процессе решения задач по математике; 2) сформированность специальных исследовательских умений, которые используются в процессе решения алгебраических и геометрических задач.
Материалы и методы исследования
Была разработана диагностическая работа для 10-х классов из семи нестандартных задач, представленных в виде теста. Варианты заданий состояли из двух частей: первая часть включала задания с выбором ответа из предложенных, вторая часть – задания, требующие развернутого решения. Всего заданий было семь. Каждое задание теста посвящено проверке уровня сформированности одного или двух исследовательских умений. Разработанный для диагностики тест был проведен на констатирующем этапе исследования
Для выполнения исследования выбраны следующие методы: 1) теоретические: анализ научных работ по обозначенной теме, систематизация и обобщение результатов решения проблемы формирования исследовательских умений разными авторами; 2) эмпирические – наблюдение, сравнение, описание, количественный и качественный анализ результатов диагностической работы.
Результаты исследования и их обсуждение
Диагностика уровня сформированности исследовательских умений старшеклассников осуществлялась посредством специально разработанного теста, содержащего семь нестандартных задач по алгебре и геометрии. В ходе исследования выделены умения, соответствующие каждой задаче.
В табл. 1 отражено соответствие между предложенными заданиями и конкретными исследовательскими умениями, подлежащими проверке.
Комплекс тестовых заданий обеспечивает проверку оценочных исследовательских умений, включающих: анализ и структурирование учебно-исследовательской деятельности; самооценку и рефлексию процесса познания; осмысление и оценку различных аспектов учебно-исследовательской работы.
Каждая задача теста представляет собой проблемную ситуацию, требующую исследования для ее разрешения. Поэтому в процессе решения школьники должны были продемонстрировать следующие общие исследовательские умения:
– на этапе выдвижения гипотезы: умение проводить серию поисковых действий для генерации рабочих гипотез, умение формулировать предположения на основе анализа условий задачи, умение верификации выдвинутых предположений через дополнительные проверки, включая опровержение с помощью контрпримеров;
– на этапе проверки гипотезы: умение устанавливать логические связи между этапами поиска решения и требованиями задачи, аргументировать каждый вывод, особенно при решении задач 4–7, контролировать соответствие полученного решения исходным условиям.
Кроме этого, задания теста были ориентированы на проверку уровня сформированности у старшеклассников специальных исследовательских умений, которые необходимы для успешного решения нестандартных математических задач. Для интерпретации результатов исследования были выделены три уровня (низкий, средний, высокий), однако следует заметить, что умения, соответствующие тестовым заданиям с выбором ответа, оценивались по двум уровням (низкий, высокий).
Соответствие исследовательских умений и их уровней представлено в табл. 2.
Приведем графическую интерпретацию результатов эксперимента по диагностике сформированности исследовательских умений обучающихся двух 10-х классов.
Результаты решения задач 1–3 представлены на рис. 1.
В процессе решения задач первой части теста проверялась сформированность умений учитывать и соотносить все данные в условии задачи, выяснять их согласованность и противоречивость. Задачи 1–3 оценивались в 1 балл в случае верного ответа и в 0 баллов в случае ошибки.
Таблица 1
Задания теста для оценки уровня сформированности исследовательских умений
|
№ п/п |
Задание теста |
Проверяемое умение |
|
1 |
Выберите из данного списка уравнения, которые являются квадратными вне зависимости от параметра p а) б) в) г) |
Умение соотнести математический объект (например, уравнение) с его определением |
|
2 |
При каких значениях параметра p уравнение
имеет единственное решение? Варианты ответа: а) -13; б) -4; в) 13; -4; г) -4; -13. |
Умение использовать знакомый алгоритм в измененной ситуации |
|
3 |
Исследуйте уравнение Варианты ответа: а) Единственное решение: нет решений при два различных корня: б) Единственное решение: нет решений при два различных корня: в) Единственное решение: нет решений: два различных корня: г) Единственное решение: нет решений: два различных корня: |
Умение исследовать задачу с параметром на количество решений |
|
4 |
При каких значениях параметра a корни уравнения
различны и оба больше -1? |
Умение находить связи между объектами задачи и определять избыточные условия |
|
5 |
При каких значениях параметра p уравнение
имеет единственное решение? |
Умение использовать знакомый алгоритм в измененной ситуации; умение провести анализ возможных случаев при решении задачи для получения верного ответа в заданных условиях |
|
6 |
При каких значениях параметра a уравнение
имеет 3 различных корня? |
Умение находить наиболее рациональный метод решения задачи, то есть заметить необходимость использования графического метода |
|
7 |
В треугольнике ABC сторона BC = 8, высота, проведенная к стороне AC, равна 6,4, а к BC – 4. Найдите длины двух других сторон треугольника ABC |
Умение выявлять все возможные выводы в соответствии с вопросом задачи; умение анализировать частные и предельные ситуации при решении задачи |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
Таблица 2
Уровни сформированности специальных исследовательских умений
|
№ п/п |
Исследовательское умение |
Уровни сформированности исследовательских умений |
||
|
Низкий |
Средний |
Высокий |
||
|
1 |
Умение соотнести математический объект с его определением |
Ученик не соотносит математические объекты с их определениями либо делает это ошибочно |
– |
Ученик соотносит математический объект с определением, преобразует объект к общему виду |
|
2 |
Умение использовать знакомый алгоритм в измененной ситуации. |
Ученик может использовать алгоритм только при решении стандартной задачи |
– |
Ученик использует известный алгоритм в новых условиях, адаптируя его шаги к построению уникального решения |
|
3 |
Умение исследовать задачу с параметром на количество решений |
Ученик не может провести анализ задачи, так как она содержит дополнительный неизвестный элемент – параметр |
– |
Ученик рассматривает все возможные случаи решения задачи в зависимости от всех возможных значений параметра |
|
4 |
Умение находить связи между объектами задачи и определять избыточные условия |
Ученик решает задачу «в лоб», придерживаясь стандартного алгоритма. Часто из-за длинных рассуждений допускает ошибку |
Ученик может провести анализ связей между объектами в задаче, составить новую математическую модель для решения, но в ней будут либо недостающие, либо избыточные условия |
Ученик проводит анализ связей между объектами в задаче, составляет новую математическую модель для решения, убирая все избыточные условия |
|
5 |
Умение провести анализ возможных случаев при решении задачи для получения верного ответа в заданных условиях |
Ученик может применить только стандартный алгоритм решения, не учитывает область существования объектов в задаче |
Ученик рассматривает только часть возможных случаев при решении задачи, некоторые из них не соотносит с областью существования объектов |
Ученик проводит анализ всех возможных случаев решения задачи, действуя в заданных условиях |
|
6 |
Умение выявлять все возможные выводы в соответствии с вопросом задачи |
Ученик рассматривает только одну, на первый взгляд, очевидную интерпретацию условия задачи |
Ученик рассматривает только одну, на первый взгляд, очевидную интерпретацию условия задачи, делает предположение о других возможных интерпретациях условия, но не рассматривает все возможные случаи |
Ученик решает задачи, рассматривая все возможные интерпретации условия |
|
7 |
Умение анализировать частные и предельные ситуации при решении задачи |
Ученик рассматривает только один очевидный, стандартный случай решения задачи, не проверяет соответствие полученного решения с начальным условием |
Ученик рассматривает несколько или все возможные случаи решения задачи, но не соотносит их с начальным условием задачи, то есть не учитывает пределы существования объектов в задаче |
Ученик рассматривает все частные случаи решения задачи, учитывает пределы существования объектов задачи, представленных в начальном условии |
|
8 |
Умение находить наиболее рациональный метод решения задачи |
Ученик может решить задачу, применяя только известный стандартный алгоритм |
Ученик подбирает другие методы решения задачи, но не может выбрать из них рациональный и часто запутывается в прямом ходе решения задачи |
Ученик подбирает различные методы решения задачи и выбирает из них наиболее рациональный, наглядный или лаконичный |
Примечание: составлена авторами на основе полученных данных в ходе исследования
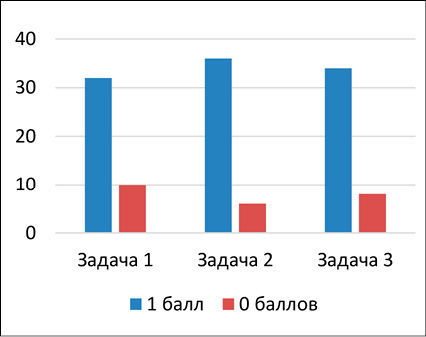
Рис. 1. Диаграмма результатов решения задач 1–3 Примечание: составлен авторами по результатам данного исследования
Соответствующие исследовательские умения оценивались по двум уровням: низкий и высокий. Результаты по первым трем задачам показывают, что большинство учеников справились с тестовыми заданиями. Последнее говорит о том, что у десятиклассников, участвующих в эксперименте, на высоком уровне развито умение учитывать и соотносить все данные в условии задачи, выяснять их согласованность и противоречивость.
Задания 4–6 проверяли сформированность поисковых исследовательских умений: умение трансформировать контекстное наполнение данной задачи и генерировать новые задачи с сохранением их общей математической структуры (задача 5 – при переходе к квадратному уравнению, задача 6 – при выборе графического метода решения); умение оценивать полноту и избыточность данных в условии задачи (задача 4 – при поиске необходимых и достаточных условий в системе для решения); умение рассматривать частные и предельные случаи в решении задачи (задача 5). Эти задачи оценивались по критериям, аналогичным критериям задач в ЕГЭ (табл. 3).
Следует отметить оценку уровня сформированности умения находить наиболее рациональный метод решения: средний уровень приводит здесь к получению не более двух баллов при решении данных задач, так как, выбирая прямой путь решения задачи (например, в задаче 6 выбрать алгебраический метод решения), старшеклассники запутываются в шагах исследования и находят минимум одно верное значение параметра, хотя их в задаче может быть несколько. Результаты решения задач 4–6 представлены на рис. 2.
Успешнее всего ученики справились с задачей под номером 6, представив графическую интерпретацию условия. Однако следует отметить, что большинство получило один и более баллов за решение задач 4 и 6. Старшеклассники начали исследование условия правильно, но далее либо допускали вычислительные ошибки, либо делали неправильные логические выводы. В задаче 5 основная ошибка заключалась в том, что они не соотносили полученные корни уравнения с ОДЗ данного уравнения.
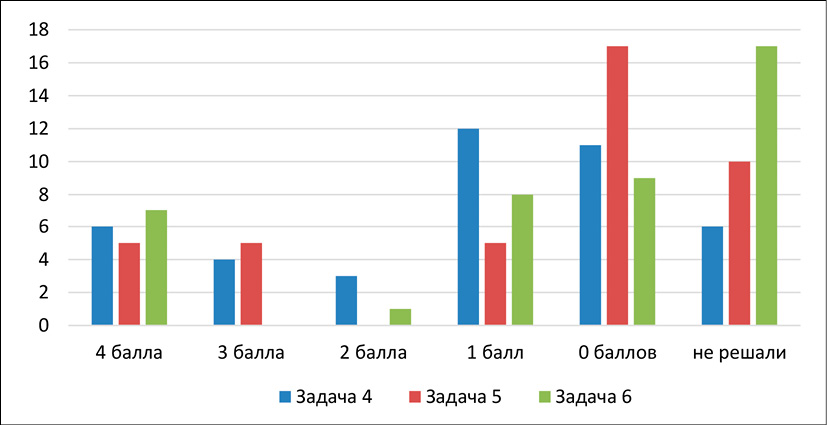
Рис. 2. Диаграмма результатов решения задач 4–6 Примечание: составлен авторами по результатам данного исследования
Таблица 3
Критерии оценки заданий 4–6
|
№ п/п |
Характеристика критерия |
Баллы |
Уровень сформированности исследовательских умений |
|
1 |
Обоснованно получен верный ответ |
4 |
Высокий |
|
2 |
С помощью верного рассуждения получены все верные значения параметра, но в ответ включены также неверные значения или решение недостаточно обосновано |
3 |
Средний |
|
3 |
С помощью верного рассуждения получено хотя бы одно верное значение параметра |
2 |
Средний |
|
4 |
Задача правильно сведена к исследованию известной модели, но дальнейшие шаги не выполнены |
1 |
Низкий |
|
5 |
Задача неправильно сведена к исследованию известной модели |
0 |
Низкий |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
Таблица 4
Критерии оценки геометрической задачи
|
№ п/п |
Характеристика критерия |
Баллы |
Уровень сформированности исследовательских умений |
|
1 |
Рассмотрены все возможные случаи решения задачи и получен верный ответ |
4 |
Высокий |
|
2 |
Не рассмотрен только один случай или допущена одна вычислительная ошибка |
3 |
Средний |
|
3 |
Рассмотрен только один случай в задаче и получен верный ответ |
2 |
Низкий |
|
4 |
Рассмотрен один случай в задаче, при верных рассуждениях допущена одна вычислительная ошибка |
1 |
Низкий |
|
5 |
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
Низкий |
Примечание: составлена авторами на основе полученных данных в ходе исследования.
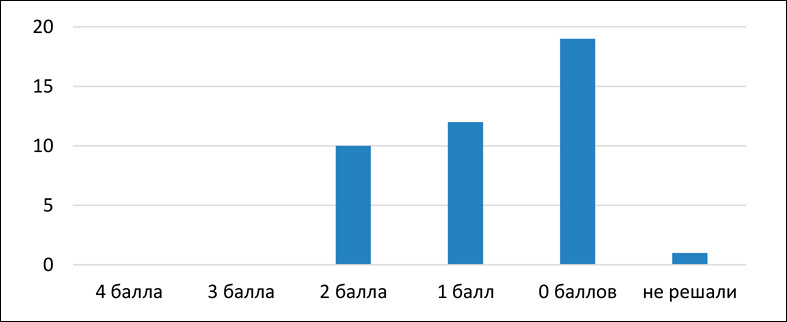
Рис. 3. Диаграмма результатов решения задачи 7 Примечание: составлен авторами по результатам данного исследования
Таким образом, у обучающихся на среднем уровне находится умение видоизменять условие задачи (как, например, в задании 6 при переходе к графической интерпретации), определять избыточные и достаточные условия в задаче. К низкому уровню относятся умения:
– сохранять общую математическую структуру, представленную в задаче, при переходе к задачам-следствиям;
– устанавливать логические связи между этапами поиска решения задачи;
– рассматривать частные случаи при решении задачи 5 (отбор корней по ОДЗ).
Проверка задачи 7 осуществлялась по критериям, которые отражены в табл. 4.
Результаты решения геометрической задачи 7 представлены на рис. 3.
Из диаграммы видно, что умения выявлять все возможные выводы в соответствии с вопросом задачи и анализировать частные и предельные ситуации при решении многовариантной геометрической задачи находятся на низком уровне.
При решении данной задачи старшеклассники рассматривали различные виды треугольников: остроугольные, тупоугольные, прямоугольные. Некоторые приходили к правильным выводам, рассматривая остроугольный и тупоугольный треугольники. Однако основная ошибка – несоотнесение полученных результатов с существованием треугольника.
Выводы
Для проверки и оценки сформированности исследовательских умений у старшеклассников возможно и целесообразно использовать нестандартные математические задачи, так как этапы их решения во многом аналогичны этапам исследовательской деятельности. Каждая такая задача представляет собой проблемную ситуацию, требующую исследования для ее разрешения. В ходе проведенного эксперимента в процессе решения нестандартных задач школьники должны были продемонстрировать как общие исследовательские умения, так и специальные исследовательские умения, которые используются в математике. Оценка последних была проведена с опорой на выделенные авторами уровни сформированности специальных исследовательских умений.
Все задачи разработанного для оценки теста проверяли также владение общими исследовательскими умениями. Проанализировав основные ошибки участников эксперимента, можно констатировать, что у учеников 10-го класса на низком уровне сформированы исследовательские умения, которые необходимы на этапе проверки гипотезы, а именно умения сопоставлять полученные результаты с исходными данными задачи, так как, переходя к частным случаям, они выходят «за рамки» области определения искомого объекта. Ученики не проводят рефлексию своих исследовательских действий, не анализируют полученные логические выводы. Такие исследовательские умения необходимы для выполнения исследовательской деятельности в любой предметной области и в решении нестандартных математических задач.
Для повышения уровня сформированности выделенных исследовательских умений целесообразно использовать в процессе обучения следующие задачи:
1. Уравнения и неравенства, которые решаются с помощью систем равносильности. Такие задачи будут способствовать формированию умения сохранять общую математическую модель, представленную в задаче, при переходе к следствиям, определять избыточные и достаточные условия.
2. Уравнения, неравенства и их системы, содержащие параметры, для рационального решения которых целесообразно применять графический метод. Подобные задания направлены на овладение умением трансформировать условие математической задачи и обоснованно выбирать рациональный метод решения.
3. Уравнения, неравенства и их системы с отбором корней по области допустимых значений или по заданному промежутку. Такие задачи будут способствовать формированию умения соотносить шаги решения задачи между собой, рассматривать все частные случаи решения, отбирать решения в рамках определенных условий.
4. Геометрические задачи на доказательство. Они будут способствовать овладению исследовательским умением на этапе проверки гипотезы – составлять логические рассуждения в рамках определенных условий.
5. Геометрические задачи на исследования различных вариантов построения чертежа, в частности задачи на построение, на поиск геометрического места точек. Такие задачи требуют проведения исследования условия для разных геометрических моделей. Они способствуют формированию умений делать все возможные выводы в соответствии с вопросом задачи; рассматривать частные и предельные случаи при решении задач.
Проблема формирования исследовательских умений обучающихся является одной из самых актуальных в среднем математическом образовании. Современные стандарты образования и тенденции развития общества требуют от будущего выпускника школы готовности к активной исследовательской деятельности. А содержание, методы и средства обучения математике в современных условиях ориентированы на организацию эффективного процесса овладения исследовательскими умениями. Структура исследовательской деятельности аналогична шагам решения нестандартных математических задач, поэтому формирование исследовательских умений школьников целесообразно ориентировать на обучение решению нестандартных алгебраических и геометрических задач.
В рамках представленного исследования была разработана методика оценки уровня сформированности исследовательских умений в процессе решения нестандартных математических задач. Она может быть использована учителями не только для диагностики, но и для создания новых вариантов нестандартных математических задач, используемых для формирования специальных и общих исследовательских умений обучающихся.
Конфликт интересов
Финансирование
Библиографическая ссылка
Капкаева Л.С., Сальникова А.С. ОЦЕНКА УРОВНЯ СФОРМИРОВАННОСТИ ИССЛЕДОВАТЕЛЬСКИХ УМЕНИЙ СТАРШЕКЛАССНИКОВ В ПРОЦЕССЕ РЕШЕНИЯ НЕСТАНДАРТНЫХ МАТЕМАТИЧЕСКИХ ЗАДАЧ // Современные наукоемкие технологии. 2026. № 1. С. 106-115;URL: https://top-technologies.ru/ru/article/view?id=40656 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/snt.40656




 ;
;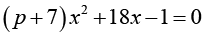 ;
;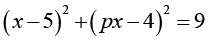 ;
;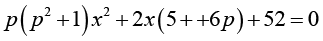
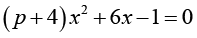
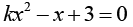 на количество решений в зависимости от параметра
на количество решений в зависимости от параметра 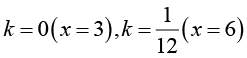 ,
,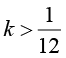 ,
,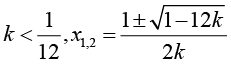 .
.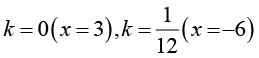 ,
,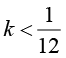 ,
,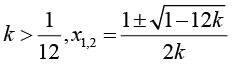 .
.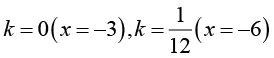 ,
,