Введение
Применение имитационных компьютерных моделей в образовательном процессе представляет собой значимое направление для улучшения качества современного обучения в различных сферах [1–3]. Имитационные модели позволяют обучающимся экспериментировать с различными сценариями в виртуальной среде, что способствует более глубокому пониманию теоретических концепций. Учащиеся могут работать в собственном темпе, повторять сложные ситуации и получать обратную связь. Имитационные модели требуют анализа ситуации, принятия решений и оценки последствий, тем самым развивая аналитические и когнитивные навыки. Использование таких моделей способствует внедрению инновационных методов обучения, повышая мотивацию и интерес обучающихся.
Для моделирования и визуализации траектории движения искусственных спутников Земли (ИСЗ) в околоземном космическом пространстве (ОКП) существует множество программных средств, включая бесплатные. Эти программы широко используются в образовательных, научных и профессиональных целях для анализа орбит, планирования запусков и обучения. Приведем некоторые примеры популярных бесплатных программ для моделирования движения ИСЗ.
Orbitron предназначен для визуализации орбит спутников в реальном времени. Позволяет отслеживать известные спутники и космические аппараты. Подходит для образовательных целей и любительских наблюдений.
Stellarium является виртуальным планетарием. С его помощью можно моделировать орбиты спутников и наблюдать их движение на небесной сфере.
Celestia – 3D-симулятор космоса. Позволяет исследовать космос, включая орбиты спутников, планет и звездных систем.
GMAT (General Mission Analysis Tool) – профессиональный инструмент для анализа и планирования космических миссий. Мощная платформа с открытым исходным кодом предназначена для моделирования орбит, траекторий и миссий.
Orekit является библиотекой для моделирования орбит, навигации и космических миссий. Программная библиотека на Java подходит для разработки собственных приложений и учебных проектов.
NASA WorldWind – виртуальный глобус для визуализации спутниковых данных и орбит. Имеется интеграция с различными данными NASA, возможность отображения орбит и траекторий.
Эти и другие похожие по назначению программы позволяют визуализировать движение спутников, понять принципы орбитальной механики, помогают планировать и моделировать космические миссии, развивают навыки работы с космическими системами и программным обеспечением. Однако все вышеперечисленные программные продукты требуют определенной квалификации и базовых знаний в области космической механики, программирования и работы с специализированным программным обеспечением. Также в условиях санкций и ограничений доступ к некоторым коммерческим или закрытым решениям может быть затруднен или невозможен.
Альтернативным подходом является разработка собственных учебных моделей [4; 5]. Для образовательных целей и в условиях ограничений важно выбирать инструменты, которые просты в использовании, не требуют глубоких технических знаний, доступны без ограничений по лицензиям или санкциям. Модель невозмущенного движения разработана авторами в [6; 7].
Цель исследования – разработать трехмерную модель движения искусственных спутников вокруг Земли, принимая во внимание форму планеты и атмосферные воздействия, и оценить эффективность ее применения в образовательном процессе.
Материалы и методы исследования
Математические методы, используемые для построения модели, изложены, например, в [8, с. 62–66; 9, c. 18–27]. Идеальное (невозмущенное) движение спутника в геоцентрической инерциальной системе координат описывается уравнением
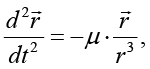
где  – радиус-вектор спутника относительно центра Земли;
– радиус-вектор спутника относительно центра Земли;
μ = GM – гравитационная постоянная G умноженная на массу Земли M,
μ ≈ 39,89∙104 км3/с2
Моделирование движения спутника в случае невозмущенного движения сводится к вычислению набора (xj, yj, zj)T точек эллиптической орбиты, j = 0..N, и вычислению моментов времени tj прохождения ИСЗ через каждую точку.
В невозмущенном движении предполагается, что спутник движется под действием только силы всемирного тяготения Земли, а сама Земля – идеальная сферическая и однородная. Уравнения движения сводятся к классическим законам Кеплера и позволяют точно описывать орбиту в течение короткого времени, когда возмущения не успевают существенно изменить орбиту, или на больших высотах с высотой полета более 36 тыс. км.
Для длительного моделирования движения спутников необходимо учитывать несферичность Земли, атмосферное сопротивление, а также гравитационные возмущения от Луны и Солнца и другие геофизические факторы.
Для учета возмущений в уравнение движения спутника вводится дополнительный вектор 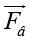 возмущающей силы
возмущающей силы
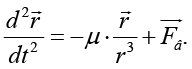
В данной работе для учета возмущений при движении искусственного спутника используется метод вариационных элементов [10, с. 340–348], основанный на предположении, что элементы орбиты являются функциями времени и изменяются под воздействием возмущающих сил. Другими словами, вместо того, чтобы считать орбиту постоянной, этот метод предполагает, что параметры орбиты (размер, форма и ориентация) меняются со временем под действием различных воздействий, таких как гравитационные возмущения других тел или неидеальности в модели. То есть параметры орбиты – это не фиксированные числа, а функции времени.
Скорости векового изменения обусловленные наличием атмосферы являются наибольшими для большой полуоси a и эксцентриситета e. Их изменение можно описать дифференциальными уравнениями
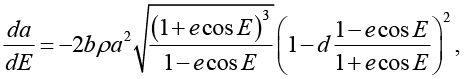
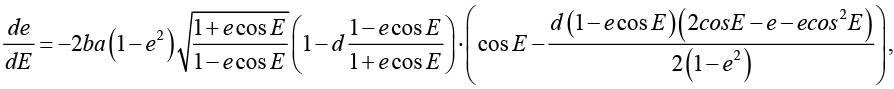
где

ρ – плотность атмосферы, E – эксцентрическая аномалия, ωz – угловая скорость вращения Земли, m – масса спутника, A – мидель (площадь наибольшего поперечного сечения) спутника, определяющая коэффициент CD, n = 2π / T – средняя угловая скорость спутника.
Плотность атмосферы ρ является функцией высоты полета [11; 12], но, с другой стороны, высота полета зависит от значения эксцентрической аномалии, так что можно считать, что ρ = ρ(E).
Положим, что известна опорная орбита. Эта опорная орбита определяется как Кеплерова (идеальная) орбита. Разделим орбиту, начиная от перигея, на N интервалов по эксцентрической аномалии. В каждом интервале можно определить
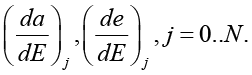
Приращения за оборот будут равны


Наибольшее влияние на долгосрочные изменения орбитальных элементов оказывает несферическая форма планеты, особенно по отношению к вековой (долгосрочной) прецессии двух ключевых параметров: долготы восходящего узла Ω и аргумента перигея ω. Чтобы определить, как изменятся эти параметры за время t, можно использовать следующие приближенные формулы:

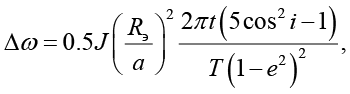
где J = 0,001624, T – период обращения спутника вокруг Земли.
Тогда за один оборот изменение элементов составит

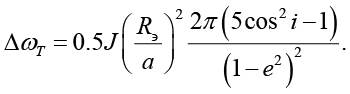
Возмущения, обусловленные сопротивлением атмосферы, для низкоорбитальных спутников также являются преобладающими.
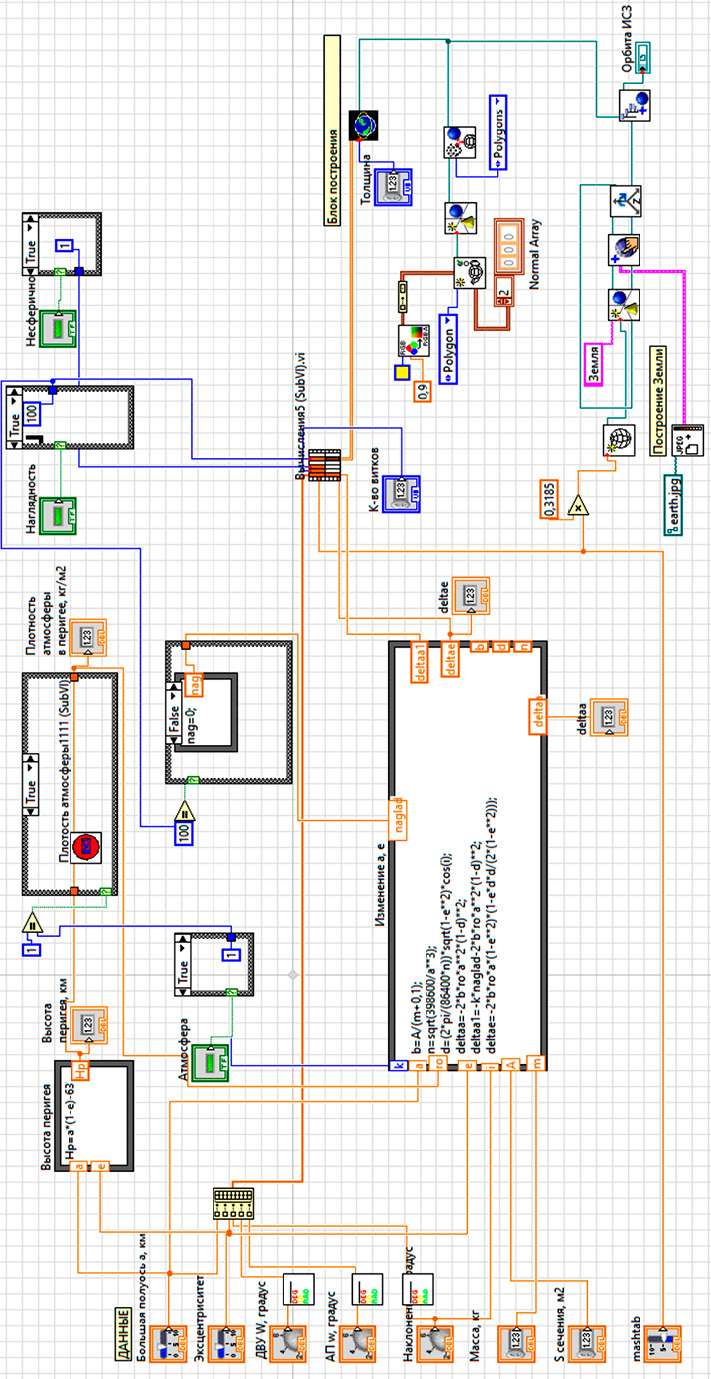
Рис. 1. Рабочая область ВП Примечание: составлен авторами по результатам данного исследования
Итак, для моделирования возмущенного движения спутника необходимо уточнять полные вековые изменения значений элементов орбиты на каждом обороте движения спутника.
Результаты исследования и их обсуждение
Модель реализована в виде виртуального прибора (ВП) с использованием графического языка программирования G, входящего в состав среды разработки LabVIEW. Среда программирования LabVIEW находит свое применение при программировании различных технических и технологических процессов [13–15].
На рис. 1 представлена рабочая область ВП, которая организована в виде набора взаимосвязанных кластеров. Левая часть схемы отведена под входные данные – элементы орбиты, параметры моделирования и настройки среды. Центральный блок прибора содержит алгоритмы построения орбиты, вычислений и визуализации, а также модули вывода данных в реальном времени. Для передачи данных между блоками используются проводники (wire), обеспечивающие синхронизацию и правильный порядок обработки информации.
Такое структурное разделение улучшает читаемость и модульность кода, облегчает отладку и дальнейшее расширение функциональности программы. Кроме того, визуальный подход в LabVIEW дает возможность наглядно проследить поток данных и логику работы модели, что особенно важно при обучении и демонстрации сложных орбитальных процессов.
Интерфейс разработанного ВП представлен на рис. 2. Параметры опорной орбиты задаются с помощью управляемых элементов – ползунков и ручек – в левой части экрана. Характеристики космического объекта определяют его масса и мидель (наибольшая площадь сечения). В нижней части экрана выводятся результаты: высоты перигея, плотности атмосферы в перигее, изменения большой полуоси, эксцентриситета за виток.
Построению траектории полета ИСЗ отведена центральная часть. Справа от области визуализации расположен ползунок, позволяющий изменять масштаб изображения.
На рис. 2 приведен пример моделирования трех витков возмущенного движения под комплексным влиянием обоих факторов: несферичности и атмосферы Земли.
Для улучшения наглядности реализована функция искусственного, искаженного усиления влияния возмущающих факторов (кнопки ON/OFF в правом верхнем углу интерфейса). Данная функциональность реализована для визуализации эволюции орбитальных параметров во времени и позволяет наглядно проследить изменения формы и ориентации орбиты под воздействием возмущающих факторов.
Интуитивно понятный интерфейс ВП обеспечивает простоту управления без необходимости длительного обучения или разработки подробной инструкции. Виртуальный прибор поддерживает непрерывный режим работы: любые изменения параметров в реальном времени отражаются на визуализации и расчетных результатах.
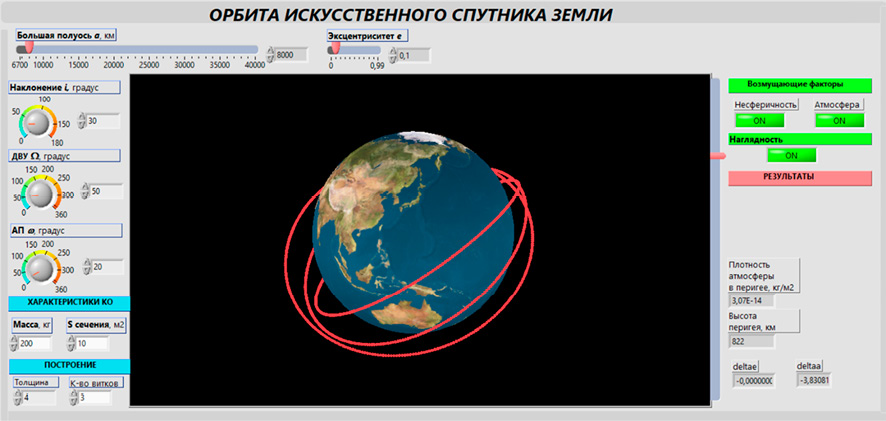
Рис. 2. Интерфейс программы Примечание: составлен авторами по результатам данного исследования
Такая возможность существенно расширяет наглядность и эффективность изучения основных закономерностей движения искусственного спутника Земли в околоземном космическом пространстве.
Использование виртуального прибора «Орбита ИСЗ с учетом атмосферы и несферичности Земли» на занятиях позволило достичь следующих целей: повысить наглядность учебного материала и устранить сложности, связанные с пространственным воображением; качественно разъяснить основные определения элементов орбиты, а также их влияние на параметры движения спутника; доступно продемонстрировать влияние несферичности Земли на траекторию движения искусственных спутников в околоземном пространстве; наглядно продемонстрировать влияние атмосферы Земли на изменение орбитальных параметров.
На практических занятиях обучающиеся могут закрепить теоретические знания, провести исследования изменений орбиты под воздействием вариаций ее элементов и временных параметров, а также изучить различия между невозмущенной и возмущенной орбитами. Разработанная модель существенно расширяет возможности интерактивного обучения и способствует более глубокому пониманию основ орбитальной динамики.
Заключение
Разработанный виртуальный прибор служит эффективным инструментом визуализации для изучения спутниковой динамики. Он обеспечивает моделирование как невозмущенного, так и возмущенного движения спутника с учетом ключевых факторов: несферичности Земли и сопротивления атмосферы. Прибор позволяет наглядно исследовать связь между параметрами орбиты и характеристиками спутника. Апробация в учебном процессе подтвердила, что его использование повышает качество и наглядность обучения.
Конфликт интересов
Библиографическая ссылка
Алдохина В.Н., Королев В.О. ВИРТУАЛЬНЫЙ ПРИБОР ПОСТРОЕНИЯ ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ С УЧЕТОМ АТМОСФЕРЫ И НЕСФЕРИЧНОСТИ ЗЕМЛИ // Современные наукоемкие технологии. 2026. № 1. С. 8-13;URL: https://top-technologies.ru/ru/article/view?id=40642 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/snt.40642



