Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 1,279

• Авторы
• Вклад авторов
• Резюме
• Файлы
• Ключевые слова
• Литература

Сидоров С.М. 1

---

1 Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет»

Сидоров С.М. - разработка концепции, работа с данными, анализ данных, проведение исследования, методология исследования, административное руководство исследовательским проектом, разработка программного обеспечения, валидация результатов, визуализация результатов, написание черновика рукописи, написание рукописи – рецензирование и редактирование

До сих пор дублирование является важным методом повышения эффективности технических систем различного назначения, а в некоторых областях – критически необходимым. Разработка математических моделей систем, обладающих сложной структурой, стохастическим характером функционирования и неполной наблюдаемостью внутренних состояний, является важной задачей. В связи с этим целью данного исследования является разработка скрытой марковской модели дублированной системы с горячим резервом и одним восстанавливающим устройством на основе ее укрупненной полумарковской модели для анализа динамики и прогнозирования состояний. Для достижения поставленной цели использовались методы математического моделирования, теории полумарковских процессов и скрытых марковских моделей. Построена полумарковская модель дублированной системы с горячим резервом и одним восстанавливающим устройством в предположении, что времена восстановления компонентов распределены экспоненциально, а времена безотказной работы имеют функции распределения общего вида. Найдено стационарное распределение вложенной цепи Маркова в явном виде, что позволило построить укрупненную модель, используя алгоритм стационарного фазового укрупнения. В статье разработана новая скрытая марковская модель дублированной системы на основе ее укрупненной полумарковской модели. Она позволяет идентифицировать отказавшие компоненты системы (по получаемой в процессе функционирования информации), прогнозировать последующие состояния, уточнять матрицу переходных вероятностей, определять наиболее вероятные последовательности состояний и др. С помощью иллюстративного примера показаны возможности разработанной модели.

Статья в формате PDF

2388 KB

дублированная система

полумарковская модель

горячий резерв

ограниченное восстановление

алгоритм стационарного фазового укрупнения

скрытая марковская модель

анализ динамики

1. Ushakov I.A. Probabilistic Reliability Models. San Diego: Wiley, 2012. 250 p. URL: https://onlinelibrary.wiley.com/doi/book/10.1002/9781118370742 (дата обращения: 03.12.2025). ISBN 978-1-11-834183-4.

2. Nakagawa T. Two-Unit Redundant Models. In: Osaki S. (eds) Stochastic Models in Reliability and Maintenance // Berlin: Springer. 2002. P. 165–191. URL: https://link.springer.com/chapter/10.1007/978-3-540-24808-8_7 (дата обращения: 03.12.2025). DOI: 10.1007/978-3-540-24808-8_7.

3. Rykov V., Efrosinin D., Stepanova N., Sztrik J. On Reliability of a Double Redundant Renewable System with a Generally Distributed Life and Repair Times // Mathematics. 2020. Vol. 8. Is. 2. P. 278. URL: https://www.mdpi.com/2227-7390/8/2/278 (дата обращения: 03.12.2025). DOI: 10.3390/math8020278. EDN: QLEQDN.

4. Malhotra R., Alamri F.S., Khalifa H.A.E.-W. Novel Analysis between Two-Unit Hot and Cold Standby Redundant Systems with Varied Demand // Symmetry. 2023. Vol. 15. Is. 6. P. 1220. URL: https://www.mdpi.com/2073-8994/15/6/1220 (дата обращения: 03.12.2025). DOI: 10.3390/sym15061220. EDN: KURWTZ.

5. Kumar N., Malik S.C., Nandal N. Stochastic analysis of a repairable system of non-identical units with priority and conditional failure of repairman // Reliability: Theory and Applications. 2022. Vol. 17. Is. 1 (67). URL: https://cyberleninka.ru/article/n/stochastic-analysis-of-a-repairable-system-of-non-identical-units-with-priority-and-conditional-failure-of-repairman (дата обращения: 03.12.2025). DOI: 10.24412/1932-2321-2022-167-123-133.

6. Obzherin Y.E., Sidorov S.M. Semi-Markov Model of a Duplicated System with Loaded Redundancy and Limited Recovery // International Journal of Reliability, Quality and Safety Engineering. 2025. Vol. 32. № 6. 2550043. URL: https://www.worldscientific.com/doi/10.1142/S0218539325500433 (дата обращения: 03.12.2025). DOI: 10.1142/S0218539325500433.

7. Obzherin Y.E., Sidorov S.M., Nikitin M.M., Glech S.G. A hidden Markov model based on superposition of two restoration processes // Automation and Remote Control. 2021. Vol. 82. Is. 6. P. 995–1012. URL: https://link.springer.com/article/10.1134/S0005117921060035 (дата обращения: 03.12.2025). DOI: 10.1134/S0005117921060035. EDN: HBYQEH.

8. Mor B., Garhwal S., Kumar A. A Systematic Review of Hidden Markov Models and Their Applications // Archives of Computational Methods in Engineering. 2021. Vol. 28. P. 1429–1448. URL: https://link.springer.com/article/10.1007/s11831-020-09422-4 (дата обращения: 03.12.2025). DOI: 10.1007/s11831-020-09422-4. EDN: AHDTFV.

9. Obzherin Y.E., Sidorov S.M., Nikitin M.M. Hidden Markov model of information system with component-wise storage devices // Lecture Notes in Computer Science. 2019. Vol. 11965. P. 354–364. URL: https://link.springer.com/chapter/10.1007/978-3-030-36614-8_27 (дата обращения: 03.12.2025). DOI: 10.1007/978-3-030-36614-8_27. EDN: OSCNAX.

10. Сидоров С.М. Скрытая марковская модель двухкомпонентной системы с групповым мгновенно пополняемым резервом времени // Информационные технологии. 2021. Т. 27. № 2. С. 64–71. URL: http://novtex.ru/IT/it2021/it221_web-64-71.pdf (дата обращения: 03.12.2025). DOI: 10.17587/it.27.64-71. EDN: EMYDGW.

11. Gámiz M.L., Limnios N., Segovia-García M.C. Hidden Markov Models in Reliability and Maintenance // European Journal of Operational Research. 2022. Vol. 304. Is. 3. P. 1242–1255. URL: https://www.sciencedirect.com/science/article/pii/S0377221722003642?via%3Dihub (дата обращения: 03.12.2025). DOI: 10.1016/j.ejor.2022.05.006. EDN: GWWJAC.

12. Королюк В.С., Турбин А.Ф. Процессы марковского восстановления в задачах надежности систем. Киев: Наукова думка, 1982. 236 с. URL: https://g.eruditor.link/file/532004/ (дата обращения: 03.12.2025).

13. Obzherin Yu.E., Boyko E.G. Semi-Markov Models: Control of Restorable Systems with Latent Failures. London: Elsevier Academic Press, 2015. 199 p. URL: https://www.sciencedirect.com/book/monograph/9780128022122/semi-markov-models (дата обращения: 03.12.2025). DOI: 10.1016/C2014-0-02226-5. EDN: VAGCXH. ISBN ‎978-0-12-802212-2.

14. Свидетельство о регистрации программы для ЭВМ № 2025686355, Российская Федерация. Программа анализа функционирования и прогнозирования состояний дублированной системы с горячим резервом и одним восстанавливающим устройством: № 2025685067: заявл. 18.09.2025: опубл. 01.10.2025 / Сидоров С.М.; заявитель Сидоров С.М. URL: https://elibrary.ru/download/elibrary_83122014_24958932.PDF (дата обращения: 03.12.2025).

15. Rabiner L.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition // Proceedings of the IEEE. 1989. Vol. 77. Is. 2. P. 257–286. URL: https://ieeexplore.ieee.org/document/18626 (дата обращения: 03.12.2025). DOI: 10.1109/5.18626.

16. Ross S.M. Introduction to Probability Models. Twelfth Edition. San Diego: Elsevier Academic Press, 2019. 826 p. URL: https://www.sciencedirect.com/book/monograph/9780128143469/introduction-to-probability-models#book-info (дата обращения: 03.12.2025). DOI: 10.1016/C2017-0-01324-1. ISBN 978-0-12-814346-9.

Введение

Высокая надежность технических систем различного назначения достигается за счет использования резервирования. Дублированная система (ДС) представляет собой систему, состоящую из двух параллельно соединенных компонентов, выполняющих общую функцию, в которой один из компонентов выступает в качестве резерва [1, с. 58]. Под горячим резервом понимается нагруженный резерв, то есть что резервный компонент тоже находится в режиме работы. В этом случае система находится в рабочем состоянии до тех пор, пока хотя бы один ее компонент работоспособен.

На протяжении последних 60 лет для моделирования и анализа ДС исследователями использовались различные случайные процессы. ДС являются основой теории надежности и могут быть найдены во многих практических приложениях, например в компьютерных системах в промышленности и военном деле, на электростанциях и распределительных устройствах, а также в системах электронных телефонных станций [2]. Обзор основных научных результатов, посвященных ДС, за период с 1960 по 2000 г. можно найти в [2]. В.В. Рыков и соавт. использовали разложимые полурегенеративные процессы с конечным множеством состояний, ограничиваясь случаем идентичных компонентов, для анализа надежности ДС с холодным резервом и одним восстанавливающим устройством [3]. Р. Малхотра и соавт., используя полумарковский процесс и методы регенерации, провели оценку и сравнение показателей надежности и эффективности двухкомпонентной системы холодного резерва и горячего резерва с одним восстанавливающим устройством [4]. Н. Кумар и соавт. получили характеристики надежности системы холодного резерва, состоящей из двух неидентичных компонентов с одним восстанавливающим устройством, в предположении, что распределения интенсивности отказов компонентов имеют отрицательную экспоненциальную зависимость, в то время как для интенсивностей восстановления приняты произвольные распределения. Для этого ими использовался полумарковский процесс и методы регенерации для исследования вероятностного поведения системы в различных возможных переходных состояниях [5]. Ю.Е. Обжерин и С.М. Сидоров разработали полумарковскую модель с дискретно-непрерывным фазовым пространством состояний дублированной системы с нагруженным резервом и ограниченным восстановлением. Это позволило получить результаты в более общем виде: в предположении, что времена безотказной работы и восстановления всех элементов системы имеют распределение общего вида [6].

Наличие у полумарковского процесса вложенной цепи Маркова (ВЦМ) позволяет построить на ее основе скрытую марковскую модель (СММ). Если предположить, что состояния системы (состояния ВЦМ) рассматриваются как ненаблюдаемые, то это приводит к задачам определения наиболее вероятной последовательности переходов состояний, прогнозированию будущих состояний на основе наблюдаемых сигналов, полученных в процессе работы системы и др. [7].

Несмотря на большую популярность использования СММ в различных реальных прикладных задачах, их применение в задачах надежности относительно невелико [8]. Однако в последние годы интерес исследователей к данной области растет. Для решения задач теории СММ применительно к моделям надежности технических систем, можно использовать метод построения СММ на основе укрупненного полумарковского процесса (ПМП) с дискретно-непрерывным фазовым пространством состояний [9; 10]. Он позволяет применять аппарат теории СММ к полумарковским моделям систем. Скрытая модель может предоставить ключевую информацию о состоянии системы, такую как отказавший компонент системы, надежность системы и связанные с этим показатели. Она также позволяет решать задачи оценки матрицы переходных вероятностей дискретной цепи Маркова и матрицы связи с сигналами [11].

Цель исследования – разработка скрытой марковской модели дублированной системы с горячим резервом и одним восстанавливающим устройством на основе ее укрупненной полумарковской модели для анализа динамики и прогнозирования состояний.

Материалы и методы исследования

Для решения задачи использовались методы математического моделирования, теории ПМП и СММ. Для разработки полумарковской модели ДС использовалась теория ПМП с дискретно-непрерывным фазовым пространством состояний (ФПС) [12, с. 44–53; 13, с. 5–7]. Сначала в работе построена полумарковская модель рассматриваемой системы, предполагая, что времена восстановления компонентов распределены экспоненциально, а времена безотказной работы заданы распределениями общего вида. Затем осуществляется переход к укрупненной полумарковской модели, применяя алгоритм стационарного фазового укрупнения [12, с. 74–79]. Это позволило перейти от дискретно-непрерывного пространства состояний полумарковской модели к дискретному и использовать аппарат теории СММ для анализа динамики укрупненной системы. Затем разрабатывается СММ рассматриваемой укрупненной системы, решаются основные задачи теории СММ.

Представленные в статье расчеты проведены при помощи разработанной автором программы ЭВМ [14] на языке Python.

Результаты исследования и их обсуждение

Описание системы. Система S состоит из двух различных компонентов K1 и K2. При построении полумарковской модели будем учитывать следующие предположения:

− В момент начала работы S оба компонента новые и начинают работать.

− Времена безотказной работы компонентов описываются случайными величинами (СВ) α1 и α2 с функциями распределения (ФР) 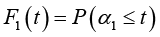, 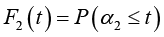и плотностями распределения f1(t), f2(t), а времена восстановления элементов – СВ β, имеющей ФР 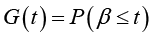и плотность распределения g(t).

− Компонент K2 находится в горячем резерве.

− Имеется только одно восстанавливающее устройство. После окончания восстановления компонент мгновенно начинает работать и считается «как новый».

− Отказ ДС наступает тогда, когда в отказе находятся оба компонента, и продолжается до восстановления одного из них.

− СВ α1, α2, β предполагаются независимыми,

,

.

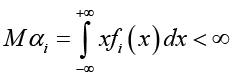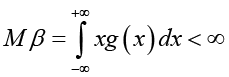Построение полумарковской модели. Опишем функционирование системы S ПМП ξ(t) с дискретно-непрерывным ФПС [6]. Вводится следующее множество E полумарковских состояний:

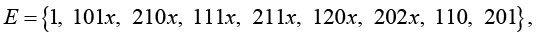(1)

где используется следующая смысловая кодировка:

− 1 определяет начальное состояние: оба компонента начинают работать;

− состояния 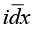представляют собой набор: i – указывает номер компонента, изменение состояния которого привело к изменению состояния системы S; компоненты вектора 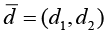определяют физические состояния компонентов системы, учитывая что

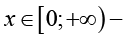определяет время до следующей смены состояния в элементе с номером отличным от i.

Например, состояние 202x означает, что изменение состояния произошло с K2: K1 восстанавливается восстановление (d1 = 0), K2 отказал и перешел в режим ожидания восстановления (d2 = 2), до момента восстановления K1 осталось время x ≥ 0.

На рис. 1 представлено функционирование системы S во времени. Периоды ожидания компонентом восстанавливающего устройства отмечены жирной линией.

Рис. 1. Функционирование системы S во времени Примечание: составлен автором в ходе исследования

Опишем ПМП ξ(t) через соответствующий ему процесс марковского восстановления (ПМВ) [12, с. 12]. Для этого нужно определить вероятности переходов ВЦМ и распределение времен пребывания на ее переходах.

Приведем вероятности переходов ВЦМ.

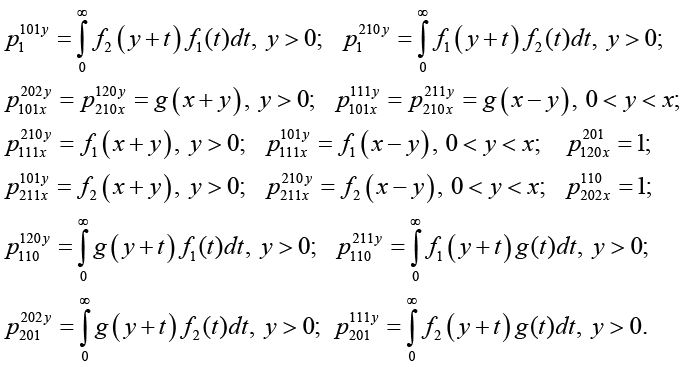(2)

Времена пребывания в состояниях системы несложно определить по рис. 2, например:

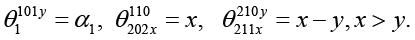
Таким образом, задан ПМВ , а следовательно, и соответствующий ему ПМП ξ(t), описывающий функционирование системы S.

Рассмотрим частный случай рассматриваемой системы, когда времена восстановления элементов имеют экспоненциальное распределение, то есть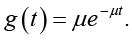

Составим систему интегральных уравнений для нахождения стационарного распределения, используя (1) и (2), в предположении существования стационарных плотностей:

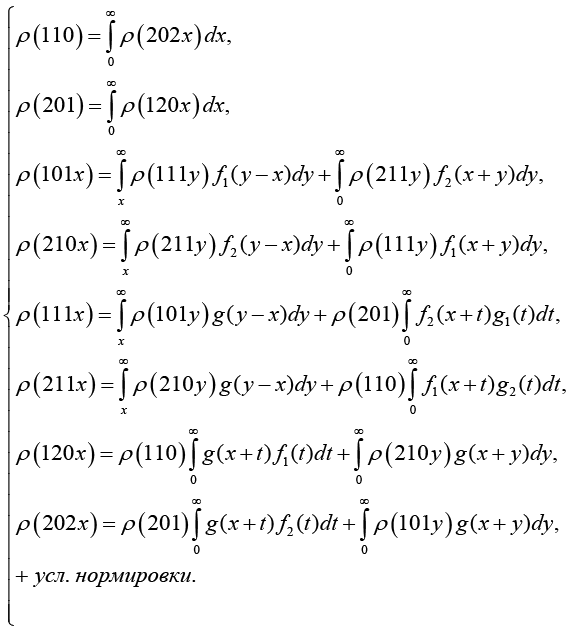(3)

Для стационарного распределения ВЦМ верна следующая лемма.

Лемма. Стационарное распределение ВЦМ 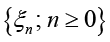, удовлетворяющее системе (3), имеет следующий вид:

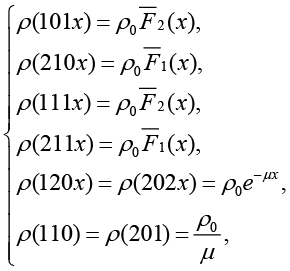(4)

где ρ0 – константа, которая находится из условия нормировки

,

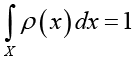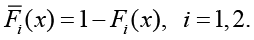
Доказательство. Покажем, что (4) является решением (3).

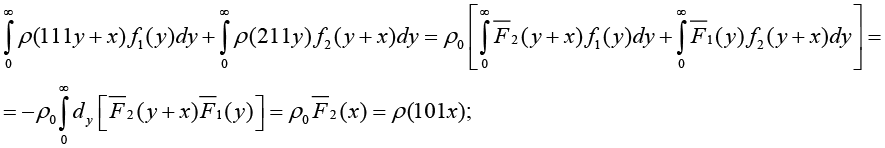
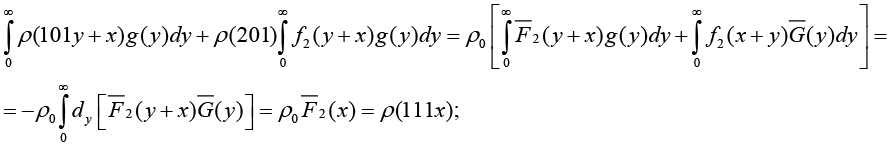
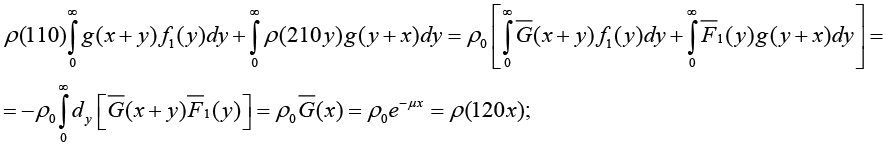
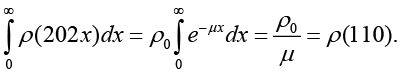
Лемма доказана.

Построение укрупненной полумарковской модели (УПММ). Построим УПММ системы S, применяя алгоритм стационарного фазового укрупнения [12, с. 74–79]. Для этого необходимо:

− задать укрупненное ФПС Ê, в соответствии с исходным ФПС;

− вычислить вероятности перехода между состояниями, входящими в Ê,

− вычислить средние времена пребывания в состояниях, входящих в Ê.

Отметим, что, так как средние времена пребывания в состояниях не используются при построении СММ, они не приводятся в работе.

Разобьем ФПС E исходной модели на N = 8 непересекающихся подмножеств таким образом, чтобы каждое из них соответствовало одному состоянию УПММ:

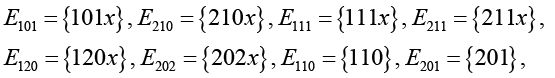
При таком разбиении коды ФПС УПММ будут иметь такой же физический смысл, что и коды ФПС E. Это объясняется тем, что мы укрупняем лишь непрерывные компоненты x для указанных классов. Следует отметить, что x неизвестны для реальных систем и задают остаточные времена действия случайных факторов, изменяющих состояния системы.

Таким образом, в этом случае ФПС Ê УПММ имеет вид

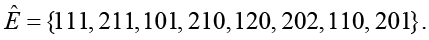(5)

Определим вероятности перехода 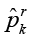между состояниями, входящими в Ê, которые, согласно [12, с. 36; 10], находятся по формуле и будут в дальнейшем использоваться для построения СММ:

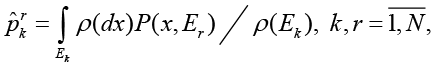(6)

где ρ(dx) – стационарное распределение ВЦМ 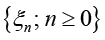, заданное формулами (4); – вероятности перехода ВЦМ .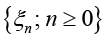

Используя формулы (2), (4), (6) и полумарковскую модель системы S, получим

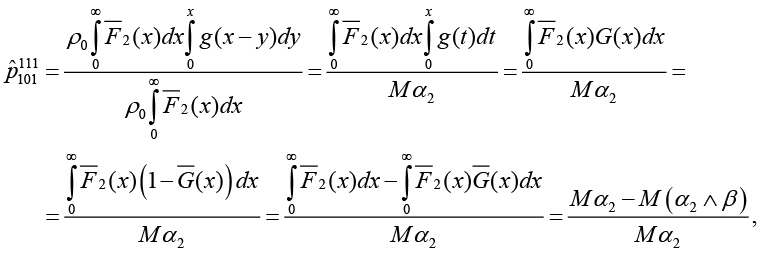
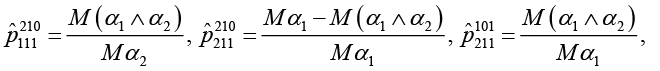(7)

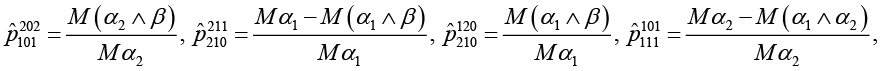
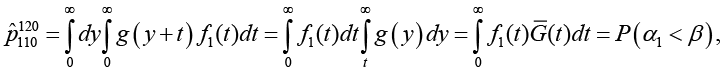
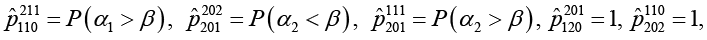
остальные 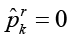, обозначает знак минимума.

Построение скрытой марковской модели. Определим СММ [9; 10]:

1. Множество состояний СММ соответствует множеству (5).

2. Матрица переходных вероятностей между состояниями системы состоит из переходных вероятностей (7).

3. Предположим, что во время функционирования системы S состояния ВЦМ укрупненной модели скрыты. Заметим, что это предположение оправдано для большинства технических систем. Зададим множество сигналов модели таким образом, чтобы сигнал соответствовал информации, которую можно было бы получить практически для любой технической системы. Тогда множество сигналов модели имеет вид

J = {0, 1, 2}, (8)

где 0 – система неработоспособна (отказ);

1 – система работоспособна: функционирует только один компонент (неизвестно, какой именно);

2 – система работоспособна: K1 и K2 функционируют.

Таблица 1

Связь R(s | x) состояний с сигналами

Примечание: составлена автором на основе полученных данных в ходе исследования.

4. Зададим связь между состояниями ВЦМ УПММ и сигналами (8), определив функцию связи R(s | x) [15], которая представлена в табл. 1. Отметим, что указанные в табл. 1 вероятности сигналов выбраны так, что сигнал для соответствующих состояний, кроме начального, может определяться с ошибкой.

5. В начальный момент времени УПММ находится в состоянии «старт», из которого она может перейти только в 101 или 210 с вероятностями

или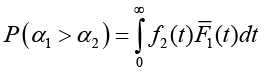

соответственно. Переходы в остальные состояния из состояния «старт» невозможны.

Пункты 1–5 полностью описывают СММ на основе УПММ.

Следуя [9; 10], используем построенную СММ для анализа УПММ. Проведем анализ и прогнозирование состояний УПММ на основе построенной СММ, следуя [15; 16, с. 269–275].

Иллюстративный пример. Рассмотрим систему S, для которой:

1) среднее время восстановления обоих элементов Mβ = 2 ч, то есть μ = 0,5;

2) средние времена безотказной работы первого и второго элементов равны Mα1 = 30 ч и Mα2 = 25 ч соответственно, а СВ α1, α2 имеют следующие распределения:

Случай 1. Эрланга IV порядка с параметрами λ1 = 2/15 и λ2 = 4/25, k = 4 (Mα1 = 30 ч, Mα2 = 25 ч).

Случай 2. Релея с параметром 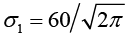и показательное с параметром λ2 = 1/25 (Mα1 = 30 ч, Mα2 = 25 ч).

Случай 3. Вейбулла с параметрами λ = 33,6; k = 3 и Эрланга IV порядка с параметром λ2 = 4/25, k = 4 (Mα1 = 30,004 ч, Mα2 = 25 ч).

Случай 4. Вейбулла с параметрами λ = 33,6; k = 3 и показательное с параметром λ2 = 1/25 (Mα1 = 30,004 ч, Mα2 = 25 ч).

Предположим, что в результате функционирования системы S получен следующий вектор сигналов (n = 30):

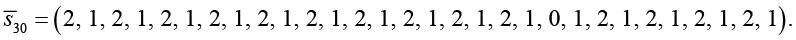
Отметим, что в силу специфики рассматриваемой модели, при задании вектора сигналов необходимо учитывать следующее:

− после сигнала «2» всегда следует сигнал «1»;

− после сигнала «0» всегда следует сигнал «1»;

− после сигнала «1» может стоять либо сигнал «2», либо сигнал «0».

С использованием разработанной СММ получены следующие результаты:

1. УПММ находилась в состояниях с соответствующими вероятностями, представленными в табл. 2, на 30-м шаге (в момент испускания 30-го сигнала).

Таблица 2

Вероятность нахождения модели в состояниях на 30-м шаге

Примечание: составлена автором на основе полученных данных в ходе исследования.

2. Прогноз состояний. УПММ переходит в следующее состояние на 31-м шаге с вероятностями (прогноз состояния), представленными в табл. 3.

Таблица 3

Прогноз состояния модели на 31-м шаге

Примечание: составлена автором на основе полученных данных в ходе исследования.

3. Сигналы на следующем 31-м шаге (прогноз сигнала) появляются с вероятностями:

случай 1: сигнал 2 с вероятностью 0,90966, 0 – 0,08034, 1 – 0,01;

случай 2: сигнал 2 с вероятностью 0,91233, 0 – 0,07767, 1 – 0,01;

случай 3: сигнал 2 с вероятностью 0,90963, 0 – 0,08037, 1 – 0,01;

случай 4: сигнал 2 с вероятностью 0,91214, 0 – 0,07786, 1 – 0,01.

4. Вероятность появления (испускания) вектора сигналов s30:

случай 1: s30 = 0,018481; случай 2: s30 = 0,017874;

случай 3: s30 = 0,018494; случай 4: s30 = 0,017918.

5. Определение наиболее вероятной последовательности смены состояний. Для вектора сигналов s30 найдем наиболее вероятные состояния (состояния с максимальной вероятностью из возможных состояний на каждом переходе) СММ на переходах. В табл. 4 указаны наиболее вероятные состояния СММ на указанных в ней переходах с соответствующими вероятностями.

Таблица 4

Состояния СММ на переходах с максимальной вероятностью

Примечание: составлена автором на основе полученных данных в ходе исследования.

Из табл. 4 видно, что на 21-м и 22-м шаге для случая 3 наиболее вероятные состояния модели отличаются от других случаев, хотя они соответствуют физическому смыслу соответствующего сигнала.

6. Проведем обучение модели, то есть уточним параметры матрицы переходных вероятностей УПММ с целью их наиболее точного согласования с полученным вектором сигналов, используя алгоритм Баума – Велша [15]. На рис. 2 представлены исходная матрица переходных вероятностей 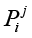и уточненная матрица переходных вероятностей 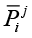, полученная в результате обучения.

Рис. 2. Матрицы 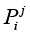и 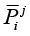для разных случаев распределения случайных величин α1, α2. Примечание: составлен автором на основе полученных данных в ходе исследования

На рис. 2 столбцы и строки приведенных матриц соответствуют состояниям «Старт», 111, 211, 101, 210, 110, 201, 120, 202 в приведенной последовательности.

Для того, чтобы определить наиболее вероятную последовательность состояний, соответствующую вектору сигналов s30, кроме выбора на каждом шаге состояния с наибольшей вероятность (как в пункте 5), можно также использовать алгоритм Витерби [15; 16 с. 273–275]. Применим его к СММ с полученными после применения алгоритма Баума – Велша уточненными матрицами переходных вероятностей. Получим следующие последовательности состояний, наилучшим образом согласующиеся с s30:

− случай 1: «старт», 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 202, 110, 211, 101, 111, 210, 211, 101, 111, 210;

− случай 2: «старт», 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 202, 110, 211, 101, 111, 210, 211, 101, 111, 210;

− случай 3: «старт», 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 202, 110, 211, 101, 111, 210, 211, 101, 111, 210;

− случай 4: «старт», 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 111, 210, 211, 101, 202, 110, 211, 101, 111, 210, 211, 101, 111, 210.

Отметим, что после обучения модели получаются одинаковые последовательности наиболее вероятных состояний для всех случаев распределения СВ α1, α2.

Заключение

В данной работе построена СММ на основе укрупненной полумарковской модели ДС горячего резервирования. Для различных распределений времен безотказной работы компонентов системы решены задачи прогнозирования последующих состояний и сигналов, определения наиболее вероятной последовательности смены состояний для заданного вектора сигналов и др. Разработанная СММ позволяет также получить решения представленных задач при различных ошибках в сигналах. Показано, что после обучения модель дает одинаковый результат для последовательностей наиболее вероятных состояний при различных случаях распределения СВ α1, α2, но одинаковых значениях Mα1, Mα2. В дальнейшем планируется построение СММ дублированных систем различной структуры и разработка СММ с непрерывными наблюдениями.

Конфликт интересов

Библиографическая ссылка