Введение
Основной целью математического моделирования сложных химических процессов является определение оптимальных условий их проведения. Зачастую оптимизация химических процессов представляет собой задачу с несколькими противоречивыми критериями: максимальный выход целевого продукта при минимальном выходе побочного продукта, при наиболее мягких условиях реакции. Постановка оптимизационной задачи при наличии нескольких критериев ранее проводилась путем исследования каждого критерия по отдельности. Например, определялись условия для максимального выхода целевого продукта. Далее определялись условия достижения экстремума по другому показателю, например объем реагентов и т.д. Получались два набора условий достижения максимума по каждому критерию. Это было ответом оптимизационной задачи [1, c. 14–18]. В условиях проведения практической реализации химической реакции полученные наборы становились труднодостижимыми, поэтому выбирался средний (компромиссный) набор условий для достижения экстремума по двум критериям [2]. Кроме того, лабораторные условия в практической реализации труднодостижимы. Ценность теоретических работ и лабораторных экспериментов по определению экстремумов реакций в реальных условиях снижается. Поэтому актуальны постановка и решение задачи одновременной многокритериальной оптимизации (МКО) в виде Парето-аппроксимации [3, 4].
Как бы ни развивались информационные технологии (увеличивалось быстродействие компьютеров, увеличивались возможности хранения данных), но моделирование химических процессов базируется на фундаментальных законах химии, физики и математики [5]. В связи с этим моделирование и последующая оптимизация должны вестись математическими методами на основе кинетической модели процесса, что позволит организовать планирование оптимального химического эксперимента и определить оптимальные условия проведения промышленного процесса. Deb K. и соавт. [6] рассматривают метод решения задачи Парето-аппроксимации методом NSGA-II на основе генетического алгоритма, который позволяет для сложных задач обеспечить приемлемую точность. D. Corne и соавт. [7] рассматривают модификации алгоритма хищник – жертва. M. Sakharov и A. Karpenko [5] на ряде известных тестовых и практически значимых задач многокритериальной оптимизации показывают сравнительную эффективность Парето-аппроксимации с помощью класса эволюционных алгоритмов с формированием фитнес-функции (функция пригодности для оценки качества каждой популяции).
Задача многокритериальной оптимизации предполагает множество решений, относящихся к паретовским решениям [8]. Лицо, принимающее решение (ЛПР), получает на основе математических расчетов совокупность компромиссных решений. Точки, входящие в решение, должны быть недоминируемые (неулучшаемые) [9].
В реальных задачах многокритериальной оптимизации (МКО) невозможно прийти к такому решению, которое было бы оптимальным для всех целевых функций, вместо него можно искать множество Парето оптимальных значений.
Множество Парето описывается формулой
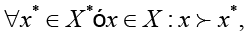
где 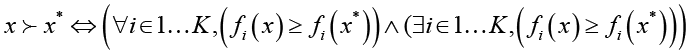 .
.
Выражение x ≻ x* означает, что x доминирует над x*: x доминирует над x* по Парето в том случае, если x не хуже x* по всем критериям и хотя бы по одному критерию превосходит x*. В таком случае в выборе x* нет смысла, так как x не только не уступает x*, но и доминирует в некоторых случаях. Если рассматривать область пространства, доминируемую решением A на примере двухкритериальной оптимизационной задачи (оба критерия максимизируются), то эта область является замкнутой, а элементы на границы решения также являются доминируемыми решением A (рис. 1).
На рис. 1 показана граница Парето для возможных решений в двухкритериальном пространстве.
Задачи многокритериальной оптимизации различаются по типу целевой функции (задачи линейного, нелинейного, квадратичного программирования), количества оптимизируемых критериев (однокритериальные и многокритериальные) и условий (условные и безусловные). От вида оптимизационной задачи зависит выбор метода решения. На рис. 2 представлена классификация методов решения оптимизационных задач [10, 11].
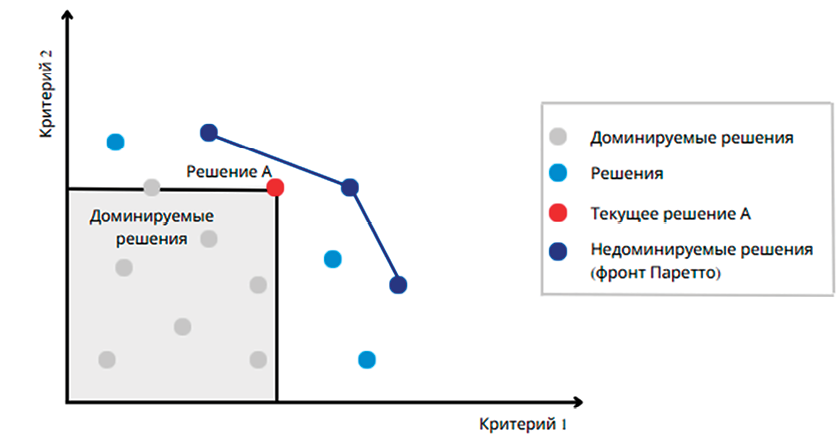
Рис. 1. Парето-аппроксимация решения многокритериальной оптимизации – фронт Парето Примечание: составлено авторами
Цель исследования – многокритериальная оптимизация условий химической реакции с выбором «идеальной» точки из всего множества Парето на примере каталитического синтеза бензилбутилового эфира.
Материалы и методы исследования
В данной работе будет рассмотрена задача условной многокритериальной оптимизации с определением решения в виде Парето-аппроксимации и выделение наилучшего значения методом «идеальной» точки.
Под «идеальной» точкой многокритериальной оптимизации в этом исследовании понимается некоторое решение, которое одновременно достигает наилучшего возможного значения для каждого из критериев оптимальности. В общем случае идеальная точка не реализуется из-за противоречивости критериев задачи, и тогда ее называют «точкой утопии».
Метод идеальной точки заключается в нахождении на границе Парето точки, ближайшей к «идеальной» точке по всем параметрам. Метод идеальной точки состоит из двух этапов. На первом этапе решаются n задач следующего вида:
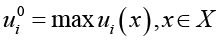 ,
,
где ui – значение целевой функции в i-й точке.
Определяется «идеальная» точка, которая в реальной задаче с ограничениями не входит в область определения, поэтому на втором этапе осуществляется поиск точки, ближайшей к идеальной (4):
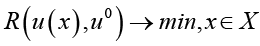 .
.
В этой формуле R – дистанционная метрика, расстояние от u(x) до u0.
В качестве дистанционной метрики принимаются различные функции [12]:
– расстояние Минковского:
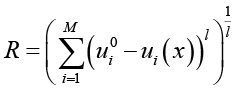 (1)
(1)
где l – параметр метрики, l ≥ 1.
– Манхэттен расстояние:
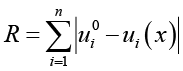 (2)
(2)
– расстояние Махаланобис:
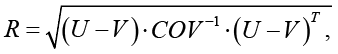 (3)
(3)
где COV – ковариационная матрица. Расстояние Махаланобис – это мера расстояния между двумя случайными точками U и V.
Элементы ковариационной матрицы cova,b рассчитываются по формуле
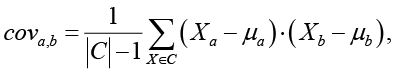
где μa и μb – математическое ожидание по признакам a и b; |C| – количество точек в классе.
Результат оптимизации напрямую зависит от выбранного метода. При использовании метода идеальной точки результатом является решение наиболее близкое к рассчитанной «идеальной» точке: максимизируется выход целевого продукта, а выход побочных – минимизируется.
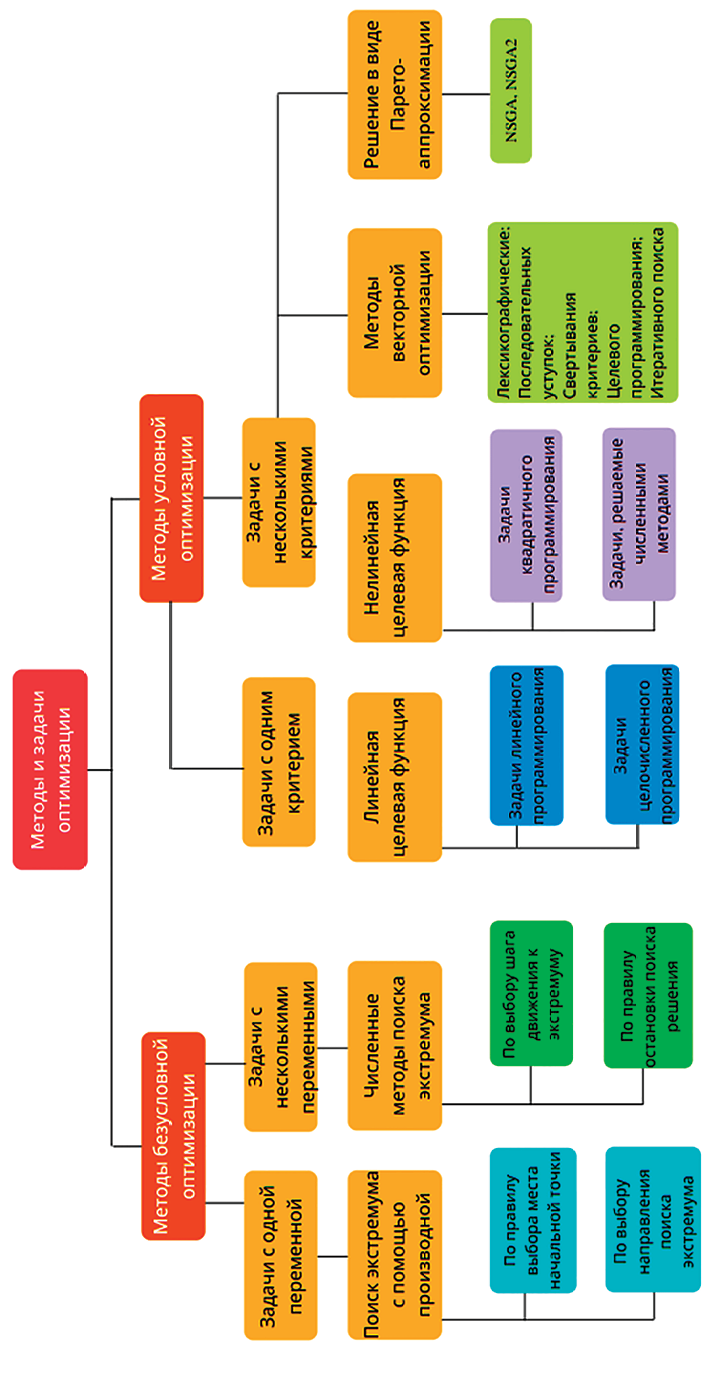
Рис. 2. Классификация методов решения оптимизационных задач Примечание: составлен авторами на основе источника [11]
Алгоритм вычисления расстояния между двумя точками:
Шаг 1. Вычислить математическое ожидание значений признаков.
Шаг 2. Вычислить среднеквадратическое отклонение значений признаков.
Шаг 3. Вычислить ковариации между парами признаков точек класса, составить ковариационную матрицу.
Шаг 4. При обратимости матрицы вычислить расстояние по Махаланобису. Если матрица необратима, используются методы для сведения матрицы к обратимой.
Из формулы (3) следует, что перед применением данного метода необходимо проверить ковариационную матрицу на необратимость. Значения ковариационной матрицы и ее определитель были рассчитаны с помощью средств языка Python.
Результаты исследования и их обсуждение
Результаты, полученные в ходе применения метода идеальной точки с применением метрики Минковского, применялись для оптимизации процесса каталитического синтеза бензилбутилового эфира [13]. Кинетическая модель была ранее разработана [14]. Бензилбутиловый эфир широко применяется в качестве ароматизатора в различных отраслях промышленности. Является крупнотоннажным, промышленным продуктом. Получение эфиров в реакции дегидратации бензилового и бутилового спиртов лучше всего проходит в присутствии катализаторов с содержанием меди, в частности CuBr2 [15]. В данной реакции происходит образование трех эфиров – бензилбутиловый (целевой), дибензиловый, дибутиловый (побочные). Поэтому задача оптимизации условий проведения реакции представляет собой многокритериальную оптимизацию с максимальным выходом целевого продукта и минимальным – побочных продуктов. На выход эфиров влияют следующие условия, которыми можно управлять через разработанную кинетическую модель: температура реакции, мольные соотношения исходных реагентов [BnOH]:[н-BuOH] и время проведения реакции.
Тогда задача МКО условий реакции синтеза бензилбутилового эфира имеет следующий вид:
– Вектор варьируемых параметров X=(x1, x2, x3), где x1 – температура реакции, T; x2 – мольное соотношение реагентов бутилового спирта к бензиловому спирту; x3 – время проведения реакции.
– Вектор функция критериев оптимальности F(X) = (f1(X), f2(X)).
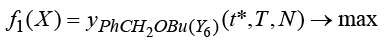 .
.
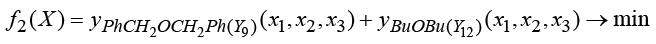 .
.
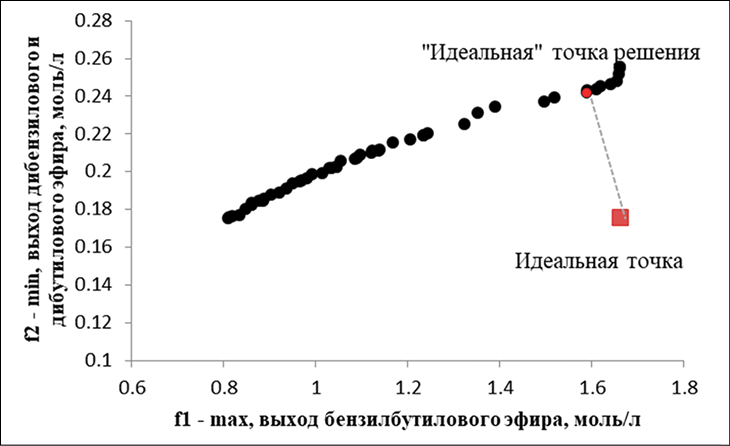
Рис. 3. Аппроксимация фронта Парето МКО-задачи реакции синтеза бензилбутилового эфира в присутствии металлокомплексного катализатора. Выбор «идеальной» точки решения Примечание: составлен авторами по результатам данного исследования
Решение задачи МКО проводилось алгоритмом Парето-аппроксимации NSGA-II в Matlab с применением распараллеливания. Условием выхода из алгоритма являлось минимальное изменение значения критерия оптимальности.
На рис. 3 приведены результаты решения задачи МКО условий реакции синтеза бензилбутилового эфира в присутствии металлокомплексного катализатора в пространстве критериев оптимальности.
На данном графике отмечена «идеальная» точка по всем параметрам. В реальных оптимизационных задачах такой исход недостижим. С помощью расстояния Минковского была найдена ближайшая к идеальной точка из решения задачи МКО.
Среди всех неулучшаемых решений МКО-задачи реакции синтеза бензилбутилового эфира в присутствии металлокомплексного катализатора можно выбрать наиболее близкую к идеальной – выделена цветом на графике фронта Парето. Для данной точки значения варьируемых параметров следующие: 167,4°C, [BnOH]:[н-BuOH] = 4:1, время реакции 694 мин. Однако, согласно определению фронта Парето, все остальные точки графика также являются оптимальными и ЛПР имеет возможность выбора.
Заключение
В работе предложен метод выбора значения из множества оптимальных, получаемых при решении задачи многокритериальной оптимизации. Однако в реальных задачах не всегда достаточно только близости решения к «идеальной» точки. Зачастую ЛПР имеет неформализованные требования к решению, потому необходимо предоставлять все множество неулучшаемых решений, с возможностью выбора.
Конфликт интересов
Библиографическая ссылка
Коледин С.Н., Коледина К.Ф. МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ УСЛОВИЙ ХИМИЧЕСКИХ ПРОЦЕССОВ С ВЫБОРОМ «ИДЕАЛЬНОЙ» ТОЧКИ // Современные наукоемкие технологии. 2025. № 11. С. 88-93;URL: https://top-technologies.ru/ru/article/view?id=40571 (дата обращения: 13.03.2026).
DOI: https://doi.org/10.17513/snt.40571



