Введение
Прогнозирование динамики цен на жилую недвижимость необходимо всем участникам рынка. Застройщикам – для того, чтобы, исходя из будущего спроса, планировать свои ресурсы и выручку; инвесторам – для того, чтобы оценивать будущую прибыль и возможные риски инвестирования; коммерческим банкам – для принятия решений по ипотечным кредитам [1]; государству – для управления развитием городской инфраструктуры; домохозяйствам – для того, чтобы осуществлять накопления и планировать кредитный потенциал [2].
Временные ряды динамики рыночных цен на недвижимость имеют некоторые особенности. В первую очередь – это нестационарные временные ряды. Стационарными в широком смысле являются временные ряды, среднее значение, дисперсия и автоковариация которых остаются неизменными. Стационарность в узком смысле – это инвариантность статистических свойств временного ряда по отношению к сдвигам во времени [3, с. 97].
Наиболее наглядным примером стационарных временных рядов являются случайные нормально распределенные процессы. Такие временные ряды легко прогнозировать, поскольку из автокорреляции можно вывести последующее значение. Таким образом осуществляются прогнозы по моделям AR (авторегрессия) и ARMA (авторегрессия – скользящее среднее) [4, с. 70]. Наличие трендовости или сезонности делает временной ряд не стационарным. В случае динамики цен на недвижимость сезонность может как присутствовать, так и нет, в зависимости от региона и других факторов, однако тренд на данных рынках присутствует обязательно по причине сочетания экономических, инфраструктурных и прочих факторов.
Следующая особенность временных рядов цен на недвижимость – это цикличность. Циклы могут быть очень длительными – до нескольких десятилетий [5]. Это связано с сильной зависимостью рынка недвижимости от макроэкономических факторов, а экономика любого государства переживает фазы подъема, пика и рецессии. Таким образом, для долгосрочного прогноза динамики рынка недвижимости необходимы нестандартные методы, учитывающие циклы.
Последняя отличительная черта временных рядов цен на недвижимость – это зашумленность [6]. Это связано в первую очередь с тем, что единой цены на объекты с одинаковыми свойствами не существует (например, две одинаковые квартиры в одном доме в одинаковом состоянии могут существенно отличаться по цене). Также шумовые колебания связаны с неоднородностью объектов. Каждый объект уникален по таким параметрам, как район, возраст здания, окружение и др.
Цель исследования – прогнозирование динамики рынка недвижимости г. Красноярска методами, учитывающими особенности временных рядов цен на недвижимость.
Материалы и методы исследования
В работе использованы авторские модификации моделей прогнозирования «Интегрированная авторегрессия – скользящее среднее» (ARIMA) и «Разложение Фурье». Первая модель была доработана автором в контексте нахождения шумовой компоненты, а вторая – в контексте выбора гармоник для реализации прогноза. Данные модели были разработаны для рынка финансовых активов [7], но могут применяться и на иных временных рядах. При этом модель ARIMA учитывает зашумленность и нестационарность, а метод «Разложение Фурье» – нестационарность и цикличность.
Модель ARIMA (p, d, q) – это модель авторегрессии – скользящего среднего (ARMA(p, d, q)), которая применяется не к значениям уровней ряда, а к разностям порядка d (для большинства временных рядов достаточно d=1). Модель ARMA (p, q) представляется следующим уравнением
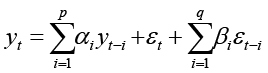, (1)
где yt – текущий уровень ряда, yt–i – уровень ряда, отстающий на лаг i, εt – ошибка модели скользящего среднего, εt–i – ошибка скользящего среднего, отстающая на лаг t-i, αi, βi – параметры модели. Первая сумма модели является компонентой авторегрессии, в вторая – компонентой скользящего среднего [8]. Для модели ARIMA формула (1) преобразуется следующим образом
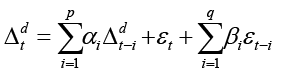, (2)
где Δd – разность порядка d. Параметр p отвечает за порядок авторегрессии, а параметр q – за порядок скользящего среднего. Для их определения используются графики частичной автокорреляции и автокорреляции соответственно [9]. Как правило, после приведения временного ряда к стационарному виду достаточно параметров p =1 и q = 1.
При создании алгоритма на основе модели ARIMA возникает задача определения шумовых компонент εi. В источниках данные компоненты определяются как гауссовский белый шум с нулевым математическим ожиданием и стандартным отклонением σ [10]. Однако необходимо знать конкретное значение σ. Автором [11] предложено определять стандартное отклонение шумовой компоненты как стандартное отклонение прогнозов по модели скользящего среднего, коэффициенты которого определяются уравнениями Юла – Уокера [4, с. 225], от фактических значений.
Параметры модели ARIMA (1, 1, 1) α и β определяются с помощью оптимизационных методов (например, метода BFGS, встроенного в Python). После того, как они определены, модель осуществляет рекуррентный прогноз по формулам (формулы представлены для модели ARIMA (1,1,1)):
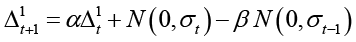
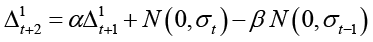
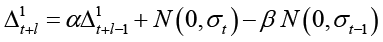, (3)
где N(0,σt) – нормальное распределение с нулевым математическим ожиданием и стандартным отклонением разностей между фактическими значениями и значениями, полученными по авторегрессионной модели, l – период прогноза.
Формулы (3) прогнозируют разницы первого порядка, а не значения уровней ряда, поэтому для верного прогноза следует применить метод накопленной суммы.
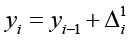, (4)
где y0 – последний фактический уровень ряда.
Разложение Фурье разделяет периодическую функцию на сумму синусоид с известными частотами, амплитудами и фазами [12]. Таким образом, если разложить временной ряд в сумму известных функций, то нетрудно будет сделать прогноз. Важно, что разложение применяется к разницам первого порядка, так как при достаточно краткосрочном прогнозе выделять периодичность в финансовых временных рядах некорректно. В общем виде разложение Фурье показано формулой 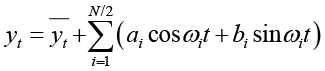(5).
, (5)
где N – период, yt – преобразованное значение временного ряда, yt – среднее значение исходного временного ряда, ωi – угловая частота i-й гармоники (первая частота соответствует периоду функции, остальные кратны ему), αi, βi – коэффициенты, которые необходимо определить. Коэффициенты ряда Фурье вычисляются по следующим формулам [13]:
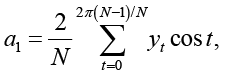
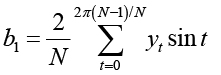(6)
для первой гармоники,
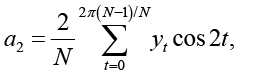
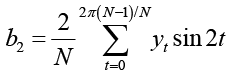(7)
для второй гармоники и так далее.
При прогнозировании временных рядов обычно выбирают гармоники с наибольшим периодом (например, первые две). Предложенная авторами модификации модели предлагает осуществлять прогноз по гармоникам не с наибольшим периодом, а с наибольшей амплитудой, что позволяет учитывать значения, выходящие за рамки нормального распределения (трех сигма) [7]. Для нахождения таких гармоник разработан алгоритм, основанный на дискретном преобразовании Фурье. Дискретное преобразование Фурье осуществляется по следующей формуле:
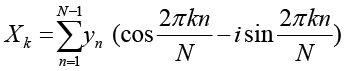, (8)
где Xk – комплексная амплитуда k-той гармоники, N – период, Ak – амплитуда k-й гармоники, yn – n-й уровень ряда, i – мнимая единица. Для определения наибольшей амплитуды достаточно действительной части числа Xk.
Таким образом, после взятия разностей первого порядка алгоритм находит действительные части амплитуд и возвращает список частот с наиболее высокими амплитудами. Амплитуды, выходящие за пределы трех сигм (стандартных отклонений), рассчитывались по формуле
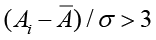, (9)
где Ai – i-я амплитуда, A – среднее значение, σ – стандартное отклонение.
Коэффициенты ai, bi находятся по формулам (6), (7) по частотам, определенным по формуле (9). При подстановке в формулы частоты следует разделить на период N. Затем полученные коэффициенты подставляются в формулу (5) и находятся прогнозные значения разниц. Последний шаг такой же, как в прогнозировании методом ARIMA – прибавление к последнему фактическому уровню ряда прогнозных разниц нарастающим итогом.
Результаты исследования и их обсуждение
Модели прогнозирования ARIMA (1, 1, 1) и «Разложение Фурье» были протестированы на динамике стоимости квадратного метра первичного и вторичного рынков недвижимости г. Красноярска за период с апреля 2010 по июль 2025 г. Расчеты производились на ежемесячных данных. Для того, чтобы проверить адекватность прогнозов и сравнить методы прогнозирования между собой, в первую очередь следует разделить исходную выборку на тренировочную и тестовую. На тренировочной выборке определяются параметры моделей, а на тестовой выборке в модель уже не подаются фактические значения. Традиционно разделение выборки на тренировочную и тестовую производится в соотношении 80% к 20% [14]. Таким образом, обучение модели производилось на данных до ноября 2021 г., а тестирование – с декабря 2021 г.
Таблица 1
Средняя абсолютная ошибка в процентах по моделям ARIMA и «Разложение Фурье», 2010 –2025 гг., помесячные данные (прогноз на 37 мес.)
|
Данные |
Средняя абсолютная ошибка, % |
|
|
ARIMA |
«Разложение Фурье» |
|
|
Стоимость кв. метра, новостройки |
12,5 |
5,7 |
|
Стоимость кв. метра, вторичное жилье |
16,4 |
3,1 |
Примечание: составлено автором на основе полученных данных в ходе исследования.
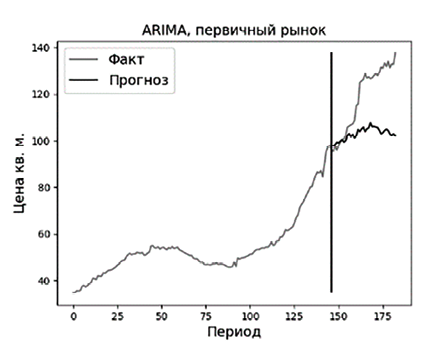
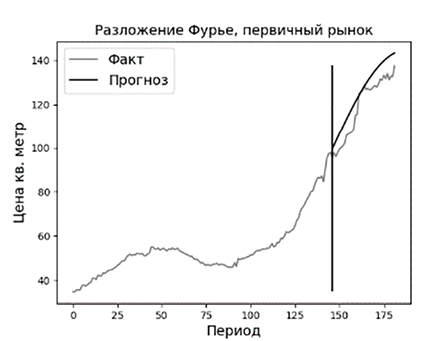
Рис. 1. Прогноз для динамики стоимости первичного жилья за 2010 – 2025 гг. методами ARIMA и «Разложение Фурье» Источник: составлено автором
Далее следует выбрать метрику, по которой оценивается точность прогноза. В регрессионных моделях, к которым относятся и модели прогнозирования, метриками точности выступают ошибки – количественные оценки предсказанных значений от фактических. К таким метрикам относятся, к примеру, средняя абсолютная ошибка (MAE), средняя квадратичная ошибка (MSE) и др. [15]. В работе была выбрана метрика MAPE (средняя абсолютная ошибка в процентах), поскольку данная метрика позволяет оценить, на сколько процентов в среднем отклоняется прогнозное значение от фактического, тогда как остальные метрики безразмерны, и их целесообразно использовать только для сравнения моделей между собой. MAPE рассчитывается по следующей формуле
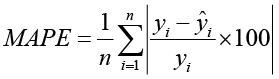, (10)
где n – число наблюдений в тестовой выборке, yi – фактическое значение показателя в тестовой выборке, ŷi – предсказанное значение показателя.
Результаты прогноза представлены в таблице 1, визуализация прогнозов для первичного рынка недвижимости представлена на рисунке 1.
Результат прогноза считается хорошим, если метрика MAPE не превышает 15%. Модель ARIMA при прогнозировании динамики вторичного рынка показала результат хуже данного порога. На первичном рынке результат модели ARIMA также не высокий, тогда как по методу «Разложение Фурье» ошибка прогноза не превысила 6%. Таким образом, на длительном промежутке времени, в котором возможен цикл, лучшие результаты показал метод «Разложение Фурье». Это объясняется тем, что метод ARIMA осуществляет прогноз, хоть исходя из зашумленных данных, но опираясь на предшествующие значения временного ряда, и разворот предсказать не может, тогда как разложение Фурье определяет периодичность ряда и может верно показать цикл.
Одной выборки недостаточно для того, чтобы делать выводы об адекватности моделей прогнозирования, поэтому для дальнейших исследований были взяты понедельные данные, а отрезок исходного временного промежутка (2010 – 2021 гг.) был разделен на 3 части: апрель 2010 – декабрь 2013; январь 2014 – сентябрь 2017; октябрь 2017 – май 2021 года.
Таблица 2
Средняя абсолютная ошибка в процентах по моделям ARIMA и «Разложение Фурье», 2010 –2025 гг., понедельные данные (прогноз на 38 недель)
|
Данные |
Период |
Средняя абсолютная ошибка, % |
|
|
ARIMA |
«Разложение Фурье» |
||
|
Стоимость кв. метра, новостройки |
апрель 2010 – декабрь 2013 |
2,3 |
7,2 |
|
январь 2014 – сентябрь 2017 |
5,9 |
2,9 |
|
|
октябрь 2017 – май 2021 |
8,1 |
9,4 |
|
|
Стоимость кв. метра, вторичное жилье |
апрель 2010 – декабрь 2013 |
1,9 |
4,5 |
|
январь 2014 – сентябрь 2017 |
3,9 |
2,6 |
|
|
октябрь 2017 – май 2021 |
6,7 |
10 |
|
Примечание: составлено автором на основе полученных данных в ходе исследования.
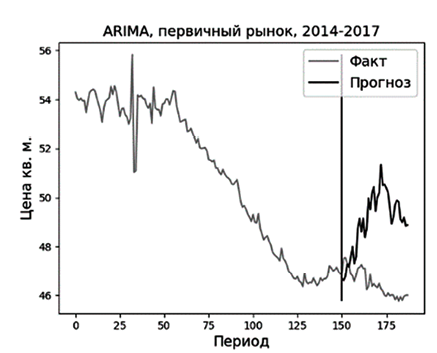
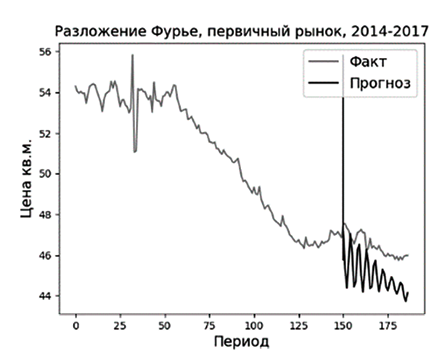
Рис. 2. Прогноз для динамики стоимости первичного жилья за 2014–2017 гг. методами ARIMA и «Разложение Фурье» Источник: составлено автором
Дальнейшие понедельные данные до 2025 г. были недоступны. Разделение на тренировочную и тестовую выборку также осуществлялось в соотношении 80:20. Результаты прогнозов в виде метрики MAPE показаны в таблице 2. На рисунке 2 в качестве примера показана визуализация прогноза с января 2024 по сентябрь 2017 г.
На более коротких временных промежутках (имеется в виду не количество элементов в выборке, а длительность во времени), на которых не может возникнуть цикл, модель ARIMA показывает хорошие результаты и в четырех случаях из шести превосходит модель «Разложение Фурье». В целом обе модели показывают небольшую среднюю абсолютную ошибку в процентах на всех исследуемых промежутках, что говорит о возможности их применения при прогнозировании динамики рынка недвижимости.
Выводы
В исследовании были проанализированы особенности временных рядов цен на недвижимость и трудности прогнозирования, которые могут возникнуть из-за данных особенностей. Временные ряды динамики рынка недвижимости нестационарны, цикличны и зашумлены. Для учета стационарности и шума в работе предложена авторская модификация модели ARIMA (интегрированная модель авторегрессии – скользящего среднего), а для учета также нестационарности и цикличности – авторская модификация метода «Разложение Фурье». Предложенные методы были протестированы на ценовой динамике стоимости квадратного метра первичного и вторичного рынков недвижимости г. Красноярска за период с 2010 по 2025 г. При этом анализ производился как за весь период по ежемесячным данным, так и за более короткие промежутки (около трех лет) по еженедельным данным. Прогнозы показали удовлетворительные результаты во всех случаях, кроме прогнозирования динамики вторичного рынка за длительный временной промежуток моделью ARIMA – ошибка составила более 16%. В качестве вывода заявлено, что методы, примененные в исследовании, учитывают особенности динамики цен на недвижимость и осуществляют качественные прогнозы как на долгосрочных, так и на краткосрочных промежутках.
Конфликт интересов
Библиографическая ссылка
Зиненко А.В. МЕТОДЫ ПРОГНОЗИРОВАНИЯ ДИНАМИКИ РЫНКА НЕДВИЖИМОСТИ // Современные наукоемкие технологии. 2025. № 11. С. 53-58;URL: https://top-technologies.ru/ru/article/view?id=40566 (дата обращения: 13.12.2025).
DOI: https://doi.org/10.17513/snt.40566