Введение
Вычислительные системы реального времени, являющиеся основой систем управления различного оборудования, управления технологическими процессами, производствами и другими объектами с высокой сложностью, требуют формирования специального теоретического описания, учитывающего специфику таких систем. Проведенные ранее исследования позволили авторам разработать формальную теорию систем реального времени [1], призванную обеспечить указанное теоретическое описание.
Согласно предлагаемому описанию, вычислительные системы реального времени служат для дискретного управления техническими системами, при котором совокупность операций управления (вычислительных операций) ограничена суммарным временем их исполнения за малый интервал времени (цикл вычислений) и доступными вычислительными ресурсами. Вариативность реализации вычислительной системы при заданных ограничениях по длительности цикла и ресурсам вычислительной системы обуславливается возможностью выбора формы представления цикла системы реального времени, то есть распределения вычислительных операций по последовательности и параллельности выполнения, по причинно-следственным отношениям, по группам исполнения для связанных вычислений и др.
Разработанная авторами формальная теория систем реального времени базируется на аксиоме о конфигурации цикла систем реального времени, содержанием которой является выбор формата представления цикла вычислений. Согласно этой аксиоме, цикл системы управления (рис. 1) определяется ее конфигурацией R, которая характеризуется распределением связанных между собой (через порты ввода и вывода данных) акторов aupi, обладающих длительностью выполнения и потребностью в ресурсах, по группам (u), потокам (p) и последовательности (i) в потоке [1]:
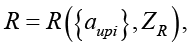(1)
где ZR – матрица портовости акторов, определяющей для каждого актора в данной конфигурации цикла минимально необходимые каналы связи с другими акторами.
Выбранный формат представления цикла вычислений, очевидно, не является единственным возможным, и в рамках предлагаемой формальной теории не доказывается его безальтернативность или оптимальность. Тем не менее выбор данного формата может быть аргументирован. Основными причинами, определившими выбор формата, являются его гибкость и аналитичность. Гибкость формата обусловлена представлением вычислительных операций (функций, задействованных в цикле вычислений) в виде квазиавтономных акторов [2; 3] или реакторов [4], а также позиционированием акторов по трем параметрам (группа, поток и последовательность в потоке), позволяющим учесть все практически значимые отношения между акторами. Аналитичность формата обусловлена возможностью формального представления цикла с определенной структурой и связями акторов, что делает возможным его математическое описание.
Сформированная на базе аксиомы о конфигурации цикла систем реального времени формальная теория позволяет решать задачу конфигурирования цикла. В некоторых случаях возможна оптимизация (нахождение конфигурации, обеспечивающей наименьшую длительность цикла вычислений или наименьшие потребные ресурсы), в других – нахождение годного (или лучшего из годных) решения, удовлетворяющего ограничениям по длительности цикла вычислений и доступным ресурсам. Также формальная теория систем реального времени позволяет оперировать портовостью как отдельных акторов, так и системы в целом, обеспечивая снижение сложности технической реализации вычислительной системы.
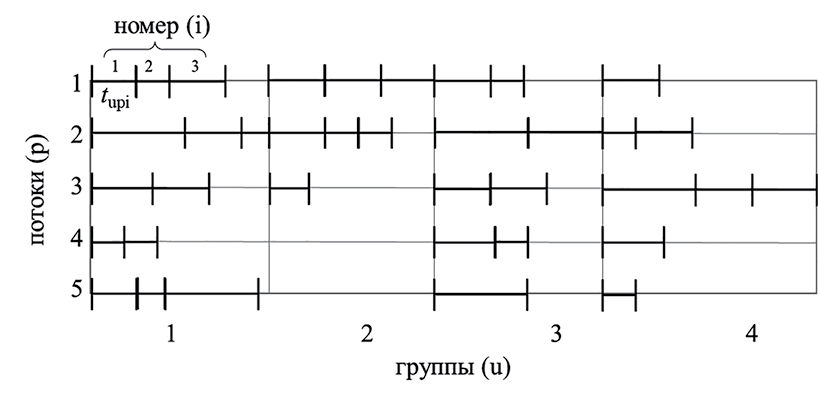
Рис. 1. Цикл системы реального времени Примечание: составлен авторами на основе источника [1]
Дальнейшее развитие формальной теории систем реального времени требует повышения определенности в отношении вычислимости формируемой системы (как композиции функций, связанных с акторами). Обеспечение вычислимости в реальном времени – задача, характеризующаяся выраженной спецификой и не имеющая до настоящего времени однозначного решения.
Целью данного исследования является расширение аксиоматики формальной теории систем реального времени, ранее разработанной авторами, исходя из требования вычислимости в реальном времени. Для этого необходимо решить следующие задачи.
Во-первых, определить подходы к обеспечению вычислимости в реальном времени, а именно определить градацию требований к используемым в системе реального времени функциям.
Во-вторых, определить требования к функциям, воспроизводимым акторами, исходя из решаемых ими задач, реализации функций в вычислительных системах и доступности конфигурирования цикла.
В-третьих, определить требования к функциям, используемым для решения задачи конфигурирования цикла, в том числе динамического, и оценить практическую реализуемость адаптивного динамического конфигурирования.
Материал и методы исследования
Исследование представляет собой теоретическую работу в основу которой положены: существующие представления о вычислимости функций в реальном времени [5], дополненные результатами исследований авторов, изложенных в предшествующих работах; разработанная авторам формальная теория систем реального времени, в логике и терминах которой проводилось представленное в статье исследование, являющееся продолжением и развитием формальной теории систем реального времени; известные [6] и предлагаемые авторами оптимизационные алгоритмы, служащие адаптивному конфигурированию цикла вычислительной системы. Для оценки возможности динамического конфигурирования цикла вычислений используется количественный анализ гетерогенной вычислительной системы с варьируемыми параметрами.
Результаты исследования и их обсуждение
Вычислимость функций в реальном времени. Согласно принятому определению, функция f с натуральными аргументами и значениями называется вычислимой, если существует алгоритм, ее вычисляющий [7, с. 9]. Однако вычислимость функции не означает, что она может быть вычислена за интервал времени, соответствующий циклу вычислений в реальном времени.
Функции, вычислимые в реальном времени, определены Хисао Ямадой [8] в терминах генераторов последовательностей (модель многоленточной машины Тьюринга) следующим образом: «Монотонно возрастающая функция U(n) называется вычислимой в реальное время, если существует генератор последовательностей, который на i-м такте печатает 1, если U(i) = j для некоторого i, и 0 в противном случае». Для того, чтобы функция была вычислима в реальном времени, она должна задаваться исключительно операторами сложения, умножения, возведения в степень и суперпозиции (подстановки функций или отождествления переменных).
Указанное ограничение обеспечивается у примитивно-рекурсивных функций. Исключение оператора минимизации (используемого для определения частично-рекурсивных функций) позволяет примитивно-рекурсивным функциям быть всюду определенными (это следует из описания оператора минимизации). Опыт синтеза вычислительных систем показывает, что это свойство (всюду определенности) является наиболее общим для функций, выполнимых в реальном времени. Заметим, что множество всюду определенных частично-рекурсивных функций (общерекурсивных функций) само не является однозначно определенным: задача по определению общерекурсивности частично-рекурсивной функции алгоритмически неразрешима. Возможны общерекурсивные функции, не являющиеся примитивно-рекурсивными (например, функция Аккермана), однако практическая значимость таких функций (по крайней мере для задач управления в реальном времени) незначительна. Поэтому допустимым является использование в качестве всюду определенных функций множества примитивно-рекурсивных функций, образующих подмножество в множестве общерекурсивных функций.
Существует, однако, альтернативный подход к обеспечению вычислимости частично-рекурсивных функций в реальном времени: посредством задания области определения функций диапазоном, в пределах которого частично-рекурсивная функция всюду определена. Такая частично-рекурсивная функция фактически становится общерекурсивной, а значит, вычислимой в реальном времени.
Ограничением для использования таких частично-рекурсивных функций с заданной областью определения является необходимость предварительной оценки ее вычислимости в пределах заданной области определения. В процессе вычислений образование такой функции не представляется возможным.
В рамках формальной теории систем реального времени область применения функций, вычислимых в реальном времени, ограничена непосредственными вычислениями, которые выполняются в пределах цикла. К таким вычислениям относятся: вычисление композиции заданных функций (соответствующих акторам) и вычисление оптимальной или годной конфигурации цикла в случае динамического конфигурирования.
В первом случае значения функций и время, необходимое для их получения, принимаются заданными. Конфигурирование цикла вычислений осуществляется исходя из возможности получения значений функций, связанных с акторами, за доступное время в пределах цикла вычислений. Используемые функции представляются в виде «черного ящика» с определенным характеристиками: функцией, временем и погрешностью ее вычисления. Внутри цикла такие функции могут задаваться в качестве функциональных модулей, внутреннее наполнение которых не рассматривается, либо как узлы диспетчеризации, через который передаются задания на вычисления функций (например, в базу данных с готовыми решениями и возможностью последующей интерполяции, либо в высокопроизводительный сопроцессор и т.д.) и получаются готовые решения.
Статическое конфигурирование цикла вычислений [1] не устанавливает ограничений на вычислимость в реальном времени – достаточно просто вычислимости. Адаптивное изменение конфигурации цикла вычислений во времени, напротив, устанавливает жесткое ограничение на используемые для конфигурирования функции. При этом необходимо констатировать, что использование функций, вычислимых в реальном времени, не гарантирует практическую реализуемость такого вычисления.
В равной степени это относится и к вычислению композиции из заданных функций. Вычислимость в реальном времени функций, используемых для вычисления композиции, не всегда означает, что композиция может быть вычислена за время цикла.
Значимым свойством функций, вычислимых в реальном времени, является возможность однозначного определения алгоритмов вычисления, а значит, априорное определение практической реализуемости вычислений в пределах цикла [9]. Мерой вычислительной сложности алгоритма является нотация (по времени и памяти/пространству), исходя из которой возможно определение необходимой длительности цикла, необходимых ресурсов (памяти/пространства) и портовости [10] вычислительной системы.
Аксиома о частично-рекурсивности функций акторов. Принятым подходом к моделированию вычислимых функций, основанным на тезисе Чёрча – Тьюринга [11, с. 283–288, 334–338], является представление вычислимых функций посредством частично-рекурсивных функций. Частично-рекурсивные функции – наиболее строго формализованная из моделей вычислений, используемых для определения вычислимых функций.
Функции, связанные с акторами, в рамках формальной теории систем реального времени должны моделироваться посредством частично-рекурсивных функций. Как мы уже установили, это не является препятствием для реализуемости вычислительной системы реального времени.
Необходимость снижения требований к определенности функций, использование функций, в общем случае не вычислимых в реальном времени, обусловлены необходимостью ограничения сложности конфигурации цикла, в наибольшей степени зависящей от количества функций (реализуемых акторами), из которых складывается композиция. Нотация сложности конфигурирования (определения оптимальной конфигурации по критерию времени, ресурсов или портовости или годной по всем критериям) цикла вычислений быстро растет по мере роста числа акторов. В частности, максимальная временная сложность алгоритма оптимизационного конфигурирования характеризуется, как показали исследования авторов, нотацией
,
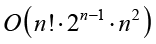где n – количество акторов.
Сокращение числа акторов (функций), реализующих в совокупности композицию, обеспечивающую требуемую функциональность вычислительной системы, невозможно без повышения сложности используемых функций.
Однозначного определения сложности функции в настоящее время не существует. Сложность определяют: на основе потребных вычислительных ресурсов (временная сложность – потребное количество шагов для вычисления, пространственная сложность – потребная память и др.), на основе минимальной длины строки, описывающей алгоритм вычисления функции (колмогоровская сложность) и др. В наиболее общем аксиоматическом представлении вычислительная сложность определяется мерой сложности Блюма [12], использующей для оценки сложности вычислимой функции, разрешимой для всей области значений переменных, ее сюръективное отображение на ту же область определения в виде геделевской нумерации. Примерами мер сложности по Блюму являются время и необходимая память для вычислений на машинах Тьюринга.
Анализ различных рекурсивных функций показывает, что наиболее заметный рост вычислительной сложности имеет место при добавлении к правилам получения функции правила минимизации, так как при переходе от примитивно-рекурсивных функций к частично-рекурсивным. Почти все сложные функции, привязанные к акторам вычислительной системы реального времени, – это частично-рекурсивные функции, лишь очень малая часть – примитивно-рекурсивные функции.
Как мы уже установили выше, для использования частично-рекурсивных функций для вычислений в реальном времени необходимо задать их область определения так, чтобы в пределах этой области частично-рекурсивная функция была всюду определена.
Исходя из констатации необходимости использования для акторов частично-рекурсивных функций, можно сформулировать вторую аксиому формальной теории систем реального времени – аксиому о частично-рекурсивности функций акторов: «функции, привязанные к акторам системы реального времени, в общем случае являются частично-рекурсивными с заданной областью определения».
Аксиома о частично-рекурсивности функций акторов, образующих цикл системы реального времени, запишется следующим образом:
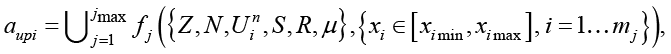(2)
где {Z, N, Uin, S, R, μ} – множество примитивов частично-рекурсивных функций: Z – ноль, N – инкремент, Uin – проекция (i-го аргумента из n), S – подстановка, R – примитивная рекурсия и μ – минимизация; {fj} – множество частично-рекурсивных функций, описывающих функцию актора aupi, xi – значение i-го аргумента функции fj, mj – количество аргументов у функции fj.
Аксиома о примитивно-рекурсивности функций конфигурирования. Наряду с функциями, привязанными к акторам, вычислительная система реального времени также определяется функциями, используемыми для конфигурирования цикла.
В случае статического конфигурирования, когда оптимальная (по заданному критерию: времени, ресурсам или портовости) или годная (по всем критериям) конфигурация вычисляется заранее, без жесткого ограничения времени, функции, используемые для конфигурирования, не обязательно должны быть вычислимыми в реальном времени (то есть за малый интервал времени, определяемый скоростью изменения объекта, для которого производятся вычисления). Однако они все равно должны быть вычислимыми за ограниченный интервал времени (хотя и не такой малый, как для вычислений в реальном времени), определяемый исходя из актуальности вычислений. Например, расчет оптимальной конфигурации вычислительной системы реального времени для управления движением рабочего органа технологического оборудования не может продолжаться слишком долго – его продолжительность ограничена сроком выполнения работ на технологическом оборудовании и периодичностью смены заданий.
С точки зрения теории вычислений качественного различия между вычислениями в реальном времени и вычислениями за ограниченное время нет. Для обоих случаев требование к используемым для конфигурирования функциям одинаковое: они должны быть всюду определенными или, если не учитывать не имеющие значительной практической значимости исключения, примитивно-рекурсивными. В случае статического конфигурирования это требование не всегда является обязательным. Однако, если требование не выполняется, заранее нельзя определить, возможно ли конфигурирование за заданный ограниченный интервал времени.
В случае динамического конфигурирования, когда конфигурация цикла переопределяется в процессе работы вычислительной системы, требования к используемым для конфигурирования функциям однозначны: они должны быть всюду определенными или примитивно-рекурсивными. В этом случае возможно заранее рассчитать, возможно ли определенное динамическое конфигурирование, а если невозможно, то скорректировать параметры конфигурирования или цикла вычислений для обеспечения реализуемости конфигурирования.
Сформулируем третью аксиому формальной теории систем реального времени – аксиому о примитивно-рекурсивности функций конфигурирования: «функции, используемые для конфигурирования цикла вычислений, должны быть примитивно-рекурсивными; для случая динамического конфигурирования удовлетворение данного требования обязательно».
Аксиома о примитивно-рекурсивности функций, используемых для конфигурирования, запишется следующим образом:
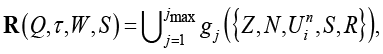(3)
где Q – композиция акторов, определяемая как совокупность двух множеств: исходного множества акторов {aj} и матрицы KQ отношений акторов исходного множества, задающей попарные отношения акторов по последовательности их выполнения;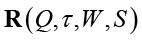 
– оператор конфигурирования цикла для заданной композиции Q по критериям τ (длительность цикла), W (используемые ресурсы) или S (портовость), {Z, N, Uin, S, R} – множество примитивов примитивно-рекурсивных функций; {gj} – множество примитивно-рекурсивных функций, используемых для задания конфигурирования.
Наряду с функциями, привязанными к акторам, вычислительная система реального времени также определяется функциями, используемыми для конфигурирования цикла. В основных формулах, положенных в основу формальной теории систем реального времени [1], используются исключительно примитивно-рекурсивные функции: сложения, вычитания, сравнения и подстановки. Следовательно, в рамках формальной теории систем реального времени аксиома о примитивно-рекурсивности функций конфигурирования выполняется. Примитивно-рекурсивность используемых для конфигурирования функций означает, что в общем случае динамическое конфигурирование возможно. Реализуемость конфигурирования в каждом отдельном случае требует количественного определения (временной) сложности алгоритма конфигурирования.
Реализуемость адаптивного динамического конфигурирования. Наиболее перспективным вариантом динамического конфигурирования является использование поискового алгоритма, основанного на адаптивном конфигурировании [13], при котором конфигурация определяется в результате многократного выстраивания конфигурации с соблюдением ограничения по суммарным ресурсам, используемым акторами. При правильной (непротиворечивой и неизбыточной) установке ограничений все годные варианты конфигурации будут включены в итоговую анализируемую выборку.
Согласно поисковой модели адаптивного конфигурирования выполнение цикла начинается с запуска p акторов, где p – число потоков в цикле. Количество вариантов запуска определяется числом сочетаний:
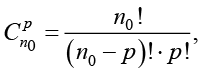(4)
где n0 – число акторов, для которых нет акторов, которые должны выполняться до них:
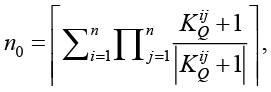(5)
где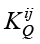 
– значение элемента матрицы отношений i-го актора с j-м, принимающего значение «–1» если j-й актор заданной композиции Q должен задействоваться до i-го, «1» – если j-й актор должен задействоваться после i-го, «0» – если порядок задействования не имеет значения.
Каждый из вариантов сочетания стартовых (первых в потоках) акторов порождает p деревьев вариантов с общим числом ветвей на концах
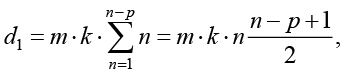(6)
где m – максимальное число вариантов выбора актора, удовлетворяющего условию ограничения используемых ресурсов, k – параметр последовательности акторов, равный среднему для различных акторов отношению количества акторов, которые должны выполняться после них или независимо от них, к общему числу акторов (использование среднего значения обусловлено оценочным характером выполняемого расчета):
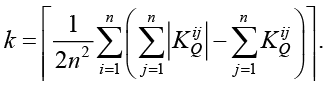(7)
Общее число вариантов для всех возможных сочетаний стартовых акторов:
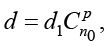(8)
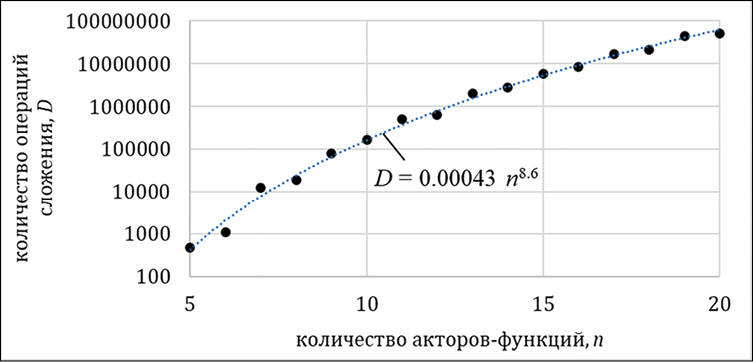
Рис. 2. Оценка необходимого количества операций сложения для конфигурирования цикла системы реального времени в зависимости от количества акторов-функций Примечание: составлен авторами по результатам данного исследования
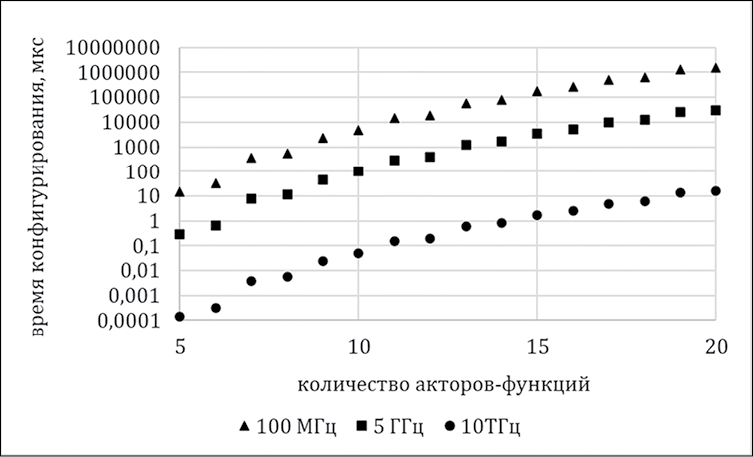
Рис. 3. Оценка времени конфигурирования цикла системы реального времени в зависимости от количества акторов-функций и тактовой частоты цифровой схемы вычислительной системы Примечание: составлен авторами по результатам данного исследования
Каждый вариант выбора при формировании предварительного множества конфигураций (сформированных в результате адаптивного конфигурирования на основе соблюдения при каждом выборе ограничения по ресурсам) верифицируется исходя из результата суммирования ресурсов для акторов на всех потоках (p). Для выбора годных по длительности цикла конфигураций необходимо суммирование длительностей выполнения всех n акторов. В результате для конфигурирования требуется общее число элементарных операций сложения, пропорциональное количеству суммируемых элементов:
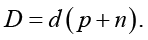(9)
Численный расчет общего числа операций сложения позволяет получить зависимость (рис. 2), примерно соответствующую D = 0,00043 n8,6. Исходные данные для оценочного расчета:
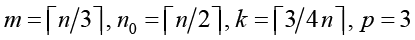
(число потоков оказывает заметное влияние на количество операций сложения лишь для малых n).
В зависимости от тактовой частоты цифровой схемы вычислительной системы изменяется длительность конфигурирования (времени, необходимого для расчета конфигурации) (рис. 3). Для оценочного расчета можно принять, что преобладающая часть вычислений – это выполнение операций сложения (операций сравнения и других на порядок меньше), и каждая операция сложения выполняется не более чем за 3 такта (обычно от 1 до 3 [1]).
При тактовой частоте, равной 100 МГц, время конфигурирования составит: 14 мкс для n = 5; 5 мс для n = 10; 180 мс для n = 15; 1,6 с для n = 20. Такая частота характерна для современных цифровых схем невысокого уровня [14].
При тактовой частоте, равной 5 ГГц, время конфигурирования составит: 290 нс для n = 5; 100 мкс для n = 10; 3,5 мс для n = 15; 31 мс для n = 20. Такая частота возможна лишь в современных процессорах высокого уровня. Для сравнения, в 2024 г. в линейках Intel и AMD наибольшая частота для х86-процессоров составила около 6 ГГц.
При тактовой частоте, равной 10 ТГц, время конфигурирования составит: 0,14 нс для n = 5; 50 нс для n = 10; 2 мкс для n = 15; 16 мкс для n = 20. Такая частота соответствует физическому пределу частот для планарной технологии цифровых схем [15].
Приведенные оценочные расчеты показывают, что возможности использования динамического конфигурирования существенно ограничены. Такое конфигурирование требует сокращения числа акторов-функций (до 12 и менее), использования цифровых схем с высокой частотой (не менее 5 ГГц).
В результате динамическое конфигурирование становится возможным для не самых быстродействующих вычислительных систем реального времени с длительностью цикла вычислений порядка 1 мс.
Выводы
На основе проведенных в статье исследований можно сделать следующие выводы:
1. Разработанная авторами формальная теория систем реального времени, призванная обеспечить теоретическое описание систем реального времени, учитывающее специфику таких систем, базируется на аксиоме о конфигурации цикла систем реального времени, содержанием которой является выбор формата представления цикла вычислений. Согласно этой аксиоме, цикл системы управления определяется ее конфигурацией, которая характеризуется распределением связанных между собой акторов, обладающих длительностью выполнения и потребностью в ресурсах, по группам, потокам и последовательности в потоке.
2. Дальнейшее развитие формальной теории требует повышения ее определенности в отношении вычислимости систем реального времени. В частности, необходимо определить подходы к обеспечению вычислимости, определить требования к функциям, воспроизводимым акторами, и функциям, используемым для решения задачи конфигурирования.
3. Проведенные исследования в области указанной проблематики позволили сформулировать две дополнительные аксиомы формальной теории систем реального времени: аксиому о частично-рекурсивности функций акторов и аксиому о примитивно-рекурсивности функций конфигурирования.
4. Оценка времени выполнения адаптивного конфигурирования, соответствующего установленным в формальной теории систем реального времени зависимостям, показала возможность динамического конфигурирования для не самых быстродействующих вычислительных систем реального времени с длительностью цикла вычислений, превышающей 1 мс.
[1] Intel® 64 and IA-32 Architectures Optimization Reference Manual: Volume 1. Document Number: 248966-050US. Intel Corporation, April 2024. [Электронный ресурс]. URL: https://cdrdv2-public.intel.com/821613/355308-Optimization-Reference-Manual-050-Changes-Doc.pdf (дата обращения: 22.09.2025).
Конфликт интересов
Финансирование
Библиографическая ссылка
Зеленский А.А., Грибков А.А. РАСШИРЕНИЕ АКСИОМАТИКИ ФОРМАЛЬНОЙ ТЕОРИИ СИСТЕМ РЕАЛЬНОГО ВРЕМЕНИ // Современные наукоемкие технологии. 2025. № 11. С. 44-52;URL: https://top-technologies.ru/ru/article/view?id=40565 (дата обращения: 13.12.2025).
DOI: https://doi.org/10.17513/snt.40565