Введение
В современном городе безопасность дорожного движения является одной из приоритетных задач, для обеспечения решения которой интеллектуальные транспортные сети играют ключевую роль [1]. Эти мобильные самоорганизующиеся сети позволяют транспортным средствам в режиме реального времени взаимодействовать друг с другом, а также с элементами дорожной инфраструктуры, что позволяет обеспечить раннее предупреждение аварий, оптимизацию транспортных потоков, повысить безопасность движения в целом [2].
Одним из важнейших компонентов системы управления городским движением являются аппаратно-программные средства фотовидеофиксации нарушений, которые не только контролируют дорожную ситуацию, но и служат источником юридически значимых доказательств при проведении административного или уголовного расследования [3]. Однако фотоматериалы и видеозаписи остаются крайне уязвимыми, так как злоумышленники могут внести в изображение изменения – затереть номер, исказить временные метки или внедрить дополнительные кадры в результат видеофиксации. С другой стороны, передача материалов фотовидеофиксации нарушений посредством публичных каналов подвергает их риску перехвата и модификации [4].
Подделка материалов фотовидеофиксации нарушений ведет к серьезным последствиям: подрывается доверие граждан к государственным органам, снижается эффективность судебных разбирательств, что в конечном итоге отражается на общей дисциплине дорожного движения [5, 6]. Кроме того, несанкционированный доступ, а также проведение анализа видеопотока может помочь злоумышленнику в раскрытии маршрута, паттернов передвижения, личной информации, что создает риски для личной и общественной безопасности.
Для противодействия этим криминальным явлениям могут применяться криптографические методы, которые обеспечивают конфиденциальность, целостность и подлинность данных. Не только простые криптографические алгоритмы могут быть уязвимы к статистическому анализу зашифрованной информации, но и криптостойкие, такие как AES, могут оставлять определенные статистические следы, которые атакующий может использовать [7, ٨]. Перспективным решением этой проблемы в условиях ограниченных ресурсов и необходимости работы в реальном времени является эффективное распределение ключей и использование быстрого потокового шифра, а также гибридных схем шифрования.
Гибридные криптосхемы, сочетающие симметричные и асимметричные алгоритмы, позволяют обеспечить баланс между скоростью обработки больших объемов видео и безопасностью при распределении ключей [2, 5, 9].
Другими важными компонентами, рекомендуемыми к реализации в модуле защиты транспортного средства, а также при доступе к хранилищу материалов фотовидеофиксации нарушений, представляются цифровые подписи, метки времени и хэширование, обеспечивающие аутентификацию и подтверждение целостности каждого видеокадра [10].
Кроме того, необходимо добиться компромисса между уровнем безопасности и производительностью комплексной системы фотовидеофиксации, которые генерируют значительные объемы данных, и их защита требует значительных вычислительных ресурсов. В связи с этим представляется целесообразным использование вычислительно простых криптоалгоритмов, оптимизированных для работы в условиях ограниченных ресурсов, а также методов селективного шифрования, которые защищают только наиболее важные компоненты материалов фотовидеофиксации нарушений (например, ключевые кадры или заголовки видеопотока, государственные регистрационные номера, лица участников и т.д.). Такой подход позволяет достичь необходимого уровня защиты при сохранении приемлемого времени отклика системы и минимальной задержки передачи, которые являются особенно значимыми [11] для обеспечения качества обслуживания пакетов в региональной ведомственной сети.
Таким образом, для обеспечения надежности, производительности и устойчивости хранилища материалов фотовидеофиксации нарушений к атакам криптографическая защита графической информации должна быть многоуровневой и сбалансированной, включающей симметричное и асимметричное шифрование, цифровые подписи, простые криптоалгоритмы и гибридные схемы [12].
Необходимо отметить, что для устройств с ограниченными ресурсами, к которым относятся транспортные средства, подходят простые потоковые криптоалгоритмы для передачи видеотрафика [13]. Устройства интернета вещей (IoT) также ограничены в ресурсах, таких как вычислительная мощность, оперативная память, заряд батареи. Как следствие, при организации сетевого взаимодействия устройств интернета вещей актуальность разработки простых потоковых криптоалгоритмов стоит особенно остро [14–16]. Алгоритмы, оптимизированные для видеопотоков интеллектуальных транспортных сетей и устройств интернета вещей, включают методы генерации ключей через генетические алгоритмы [17] и схема защиты контента с использованием селективного шифрования, обеспечивающие защищенное кодирование без полного дешифрования [18]. В предложенной схеме ключ дешифрования не требуется предоставлять на промежуточных устройствах и в облачном центре обработки данных.
Цель исследования – разработка параметрического метода скремблирования изображений на основе преобразования Арнольда, преодолевающего ограничения классического подхода и повышающего устойчивость систем к криптоанализу.
Материалы и методы исследования
Исследование выполнено на кафедре ЭВМ и систем в Волгоградском государственном техническом университете в 2024–2025 гг. Объектом исследования являлись цифровые изображения, полученные системами фотовидеофиксации нарушений дорожного движения. Методологической основой послужило математическое моделирование преобразования Арнольда и его параметрической модификации. В программной реализации применялись методы линейного отображения дискретных множеств. Для оценки результатов был проведен статистический анализ корреляционных связей между пикселями изображений. Эффективность предложенного метода оценивалась с помощью анализа метрик декоррелирующего воздействия преобразования на исходные цифровые изображения.
Результаты исследования и их обсуждение
В 1960-е гг. выдающийся советский математик Владимир Игоревич Арнольд, предложил двумерное отображение с фазовым пространством в виде тора, проиллюстрировав его на примере изображения головы кошки. Двумерное отображение Арнольда представляет собой классическое линейное отображение точек двумерной решетки, определенной на дискретном множестве, и получило популярность для скремблирования [19, 20]. Необходимо отметить, что отображение Арнольда также применяется в качестве одного из этапов в стеганографических алгоритмах для защиты графической информации [21–23].
Каждый элемент множества описывается координатами (x,y), где N – размерность множества и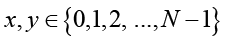 
.
Отображение Арнольда может быть записано в виде
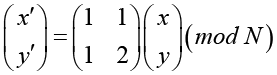
или в развернутом виде
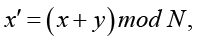
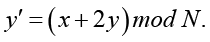
Здесь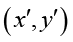 
– координаты пикселя после итерации линейного отображения. Отображение является обратимым, так как
.
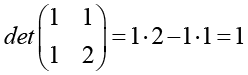Результат вычисления преобразования Арнольда показан на рис. 1.
Рис. 1. Результат вычисления преобразования Арнольда Источник: составлено авторами по результатам данного исследования
Преобразование Арнольда эффективно разрушает пространственные зависимости, но обладает рядом ограничений. В силу фиксированности матрицы отображение имеет предсказуемую структуру и фиксированный период. Если известны габариты изображения, злоумышленник может перебором итераций восстановить исходное изображение. Кроме того, пространство ключей у классического варианта преобразования Арнольда ограничено только числом итераций, что делает его потенциально уязвимым для атак грубой силы.
Для преодоления указанных ограничений предлагается обобщенная форма параметризованного преобразования Арнольда с дополнительными параметрами ϑ1 и ϑ2. В этом случае отображение Арнольда будет описываться как
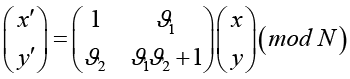
или (в развернутом виде) как
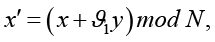
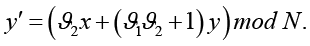
Здесь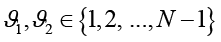 
– оказывающие значительное влияние на динамику и периодичность преобразования параметры, которые могут выступать частью секретного ключа. Обратимость обобщенного преобразования также сохраняется при условии, что определитель матрицы преобразования равен 1:
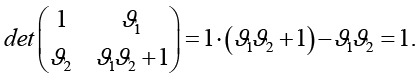
С целью анализа эффективности предлагаемой методики защиты графической информации проводится исследование влияния параметров преобразования Арнольда на оказываемое декоррелирующее воздействие на исходное изображение. При вычислении преобразования Арнольда осуществляется сравнение результирующего изображения с исходным с целью расчета меры вносимых искажений.
Для вычисления статистически значимой связи между соседними пикселями в полученных после вычисления преобразования Арнольда воспользуемся выборочным коэффициентом корреляции Пирсона для n-выборки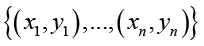 
:
.
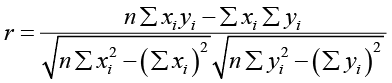Рис. 2. Корреляция пикселей для различных преобразований Источник: составлено авторами по результатам данного исследования
Примеры результатов вычисления 1 итерации параметрического преобразования Арнольда с различными ϑ1 и ϑ2, а также корреляции между соседними пикселями показаны на рис. 2.
Как видно из рисунка, в результате вычисления 1 итерации оригинального преобразования Арнольда с ϑ1 = 1 и ϑ2 = 1 статистически значимая связь между пикселями сохраняется, выборочный коэффициент корреляции Пирсона r = 0.8391. Помимо значения метрики зависимость между соседними пикселями также хорошо видна на рисунке. Для других пар параметров (5,9) и (11,9) видно, что связь между пикселями нарушается, и преобразование оказывает значительное декоррелирующее воздействие на исходное изображение, что подтверждается и значениями коэффициента корреляции: r = 0.3006 и r = –0.0444 соответственно.
Таким образом введение параметров ϑ1 и ϑ2 значительно расширяет функциональные возможности преобразования Арнольда и устраняет многие его ограничения. Одним из основных преимуществ является существенное увеличение пространства ключей. В классическом преобразовании Арнольда ключевой параметр фактически один – число итераций. В параметрическом варианте преобразования добавляются параметры, принимающие множество значений. Наблюдается экспоненциальный рост пространства ключей, что делает атаку полного перебора параметров чрезвычайно затруднительной.
Благодаря введению параметров ϑ1 и ϑ2 нарушается предсказуемость структуры преобразования и усложняется анализ периодичности. Даже если атакующий знает число итераций, без сведений о значениях параметров ϑ1 и ϑ2 восстановление исходного изображения становится чрезвычайно затруднительным.
Параметры преобразования влияют на характер перестановки пикселей, что позволяет адаптировать предложенное преобразование под конкретные требования к скорости, типу скремблирования и устойчивости к статистическому анализу.
В классическом преобразовании период зависит только от размера изображения и может быть заранее вычислен. В предложенном подходе период является функцией не только N, но и параметров ϑ1 и ϑ2, что делает его сложно предсказуемым.
Таким образом, предложенное преобразование сохраняет все свойства преобразования Арнольда: остается обратимым, не изменяет значения яркости пикселей и имеет эквивалентную вычислительную сложность.
Заключение
В настоящей работе было проведено исследование, посвященное анализу актуальной проблемы защиты графической информации в интеллектуальных транспортных системах с фотовидеофиксацией нарушений дорожного движения. Учитывая ключевую роль таких данных в обеспечении правопорядка и общественной безопасности, их защита от несанкционированного доступа и подделки является стратегически важной задачей. Показано, что применение традиционных криптографических алгоритмов, несмотря на их высокую криптостойкость и устойчивость к статистическому анализу, сопряжено с существенными ограничениями при использовании в сетях с быстро изменяющейся топологией и в условиях реального времени. Высокая вычислительная сложность делает их малопригодными для внедрения в конечные устройства с ограниченными ресурсами, к которым относятся транспортные средства и элементы дорожной инфраструктуры.
В ходе исследования показано, что преобразование Арнольда может служить эффективным инструментом для скремблирования изображений, но классический вариант преобразования обладает рядом недостатков, позволяющих злоумышленнику восстановить исходное изображение путем перебора итераций. Для преодоления ограничений предложена параметрическая модификация классического преобразования, существенно затрудняющая проведение криптоанализа. Полученные результаты показали, что пространственная корреляция между пикселями статистически незначительна, что подтверждает высокую эффективность декоррелирующего воздействия предлагаемого преобразования.
Конфликт интересов
Библиографическая ссылка
Земцов А.Н., Кузнецов М.А., Садек Сажжад, Пшеничный Д.С., Майданников К.А. ПАРАМЕТРИЧЕСКИЙ МЕТОД СКРЕМБЛИРОВАНИЯ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ АРНОЛЬДА // Современные наукоемкие технологии. 2025. № 10. С. 46-51;URL: https://top-technologies.ru/ru/article/view?id=40526 (дата обращения: 15.11.2025).
DOI: https://doi.org/10.17513/snt.40526