Введение
Задачи оптимизации играют фундаментальную роль в широком спектре научных и промышленных приложений, включая логистику, финансы, телекоммуникации и разработку лекарственных препаратов. Многие критически важные проблемы в этих областях относятся к классу NP-трудных задач, что делает их вычислительно неразрешимыми для больших объемов данных. Классические алгоритмы для сортировки и поиска, такие как QuickSort (быстрая сортировка), MergeSort (оптимизация слиянием) и Binary Search (бинарный, или двоичный, поиск), разрабатывались и оптимизировались на протяжении десятилетий для достижения максимальной эффективности. Современная предметная плоскость оптимизации охватывает широкий спектр методов, включая оптимизацию роя частиц, алгоритм мотылька и пламени, а также генетический алгоритм – каждый из которых реализует уникальный подход к поиску наилучших решений [1].
Однако, несмотря на весомые достижения в области классических методов оптимизации, решение NP-трудных задач по-прежнему является проблематичным, поскольку применение точных методов зачастую оказывается нецелесообразным из-за их экспоненциальной вычислительной сложности при увеличении размерности. Кроме того, получившие широкое распространение алгоритмы традиционно реализовывались на классических вычислительных системах, которые, несмотря на свою эффективность, сталкиваются с ограничениями в скорости обработки данных и мощности.
С учетом вышеотмеченного не подлежит сомнению тот факт, что с геометрическим ростом объемов информационных массивов и появлением новых областей, таких как искусственный интеллект, большие данные и облачные сервисы, возникает потребность в новых алгоритмах оптимизации, способных справиться с постоянно растущими вычислительными требованиями. В данном контексте огромный потенциал для решения сложных задач демонстрируют алгоритмы квантовой оптимизации, появление которых стало важной вехой в вычислительной науке. С развитием квантовых схем многие вопросы, включая сортировку и поиск, могут получить экспоненциальное ускорение благодаря таким свойствам квантовой механики, как квантовая суперпозиция, запутанность и квантовая интерференция.
С момента разработки вариационных квантовых алгоритмов (VQA) и их подклассов, таких как вариационный квантовый эйгенисовер (VQE) и алгоритм квантовой приближенной оптимизации (QAOA), количество научных работ, посвященных практическому применению методов обработки данных на квантовом уровне, с каждым годом увеличивается. Особый интерес представляют приложения математической оптимизации, и QAOA широко используется в этом контексте. Хотя QAOA является эвристическим методом, исследователи постоянно совершенствуют его, внося небольшие улучшения и точные корректировки для достижения лучшей производительности при решении узких оптимизационных задач. Наиболее часто встречающимися задачами являются задача коммивояжера (TSP) и задачи разбиения графов, такие как MaxCut. Благодаря квантовой логической последовательности эти NP-трудные задачи могут быть сведены к квадратичной неограниченной бинарной оптимизации (QUBO) или формулировкам Изинга [2].
Потенциальные преимущества квантовых алгоритмов в решении сложных оптимизационных задач сделали рассматриваемую проблематику очень популярной в научно-экспертном сообществе. Об этом свидетельствует значительное внимание, уделяемое ей со стороны ученых и практиков. Однако вокруг этой темы существует ряд заблуждений, особенно в отношении скорости и универсальности оптимизационных задач, которые могут быть решены. Хотя аргументированным является утверждение, что квантовые компьютеры потенциально могут решать некоторые задачи быстрее, чем классические, истинное квантовое преимущество еще не было доказано на практике [3]. Кроме того, в отличие от классической оптимизации, где существуют хорошо отработанные тесты для оценки решателей, в квантовой оптимизации до сих пор отсутствуют стандартизированные методологии и наборы данных, которые могли бы надежно оценить эффективность и масштабируемость квантовых подходов.
Таким образом, вопросы, связанные с систематическим сравнением алгоритмов, оценкой возможностей оборудования и пониманием практических преимуществ квантовой оптимизации по сравнению с классическими методами, имеют высокую научно-практическую значимость, что и послужило стимулом для выбора темы данной статьи.
Цель исследования – провести сравнительный анализ алгоритмов оптимизации в контексте классических и квантовых вычислительных моделей.
Материалы и методы исследования
Результаты исследования относительной производительности классических алгоритмов оптимизации в трех вычислительных конфигурациях: локальном классическом компьютере, локальной классическо-квантовой интегрированной системе и квантовом компьютере IBM – представлены публикациями С.В. Пальмова, А.А. Каретиной, А.А. Шайдуллиной [4], Bidisha Dhara, Monika Agrawal [5], С.М. Гушанского, В.С. Потапова [6].
Над разработкой надежных тестов, которые позволяют отличить реальные улучшения квантовых алгоритмов от артефактов, вызванных особенностями оборудования, а также преодолеть разрыв между теоретическими перспективами и практическим применением квантовых вычислительных подходов, трудятся Ш. Галандарова, Ю. Эрметов, Б. Реджебов, А. Тиркешова [7], А.В. Чуваков, Р.О. Боряев [8], Fabian Langkabel, Pascal Krause, Annika Bande [9].
Обзор различных расширений и вариаций алгоритма квантовой приближенной оптимизации, стратегии улучшения его параметров, анализ эффективности и производительности алгоритма в различных примерах задач входит в круг научных интересов Steve A. Abel, Andrei Constantin [10], В.В. Масленникова, Л.А. Демидовой [11], С.В. Ульянова, Н.В. Рябова, П.В. Зрелова [12], Jie Xu, Dingjun Qian, Gensheng Hu [13].
Несмотря на многообещающие перспективы и активный интерес ученых к рассматриваемой проблематике, остается еще широкий перечень серьезных и нерешенных проблем. Так, например, на данный момент в литературе по-прежнему существует множество противоречивых мнений по различным аспектам квантовых алгоритмов: например, по каким задачам эти вычисления могут превзойти классические подходы, если таковые имеются, и могут ли они обеспечить какое-либо практическое преимущество в условиях шума и ошибок современных квантовых устройств. Отдельного внимания заслуживают компромиссы между качеством решения, временем выполнения и использованием ресурсов, что позволит обеспечить целостное представление о производительности квантовой оптимизации.
Методы исследования: анализ и обобщение, сравнение, прогнозирование, моделирование, систематизация, формально-логический подход.
Результаты исследования и их обсуждение
Область классической оптимизации охватывает много конкретных задач, которые часто имеют полезные практические применения в самых разных областях науки и техники. В зависимости от того, являются ли переменные дискретными или непрерывными, задачи оптимизации можно разделить на три класса: дискретная оптимизация, непрерывная оптимизация, а также комбинаторная оптимизация, которая многократно усложняется вследствие широкого спектра целевых функций и типов ограничений [14]. В соответствии с этими задачами классифицируются и соответствующие алгоритмы.
Так, например, для небольших задач предпочтительными являются точные методы, поскольку они могут гарантировать оптимальность. Однако для больших задач точные методы могут стать вычислительно невыполнимыми, и для поиска хорошего решения в разумные сроки используются приближенные методы. Многие задачи комбинаторной оптимизации, как известно, относятся к классу APX-сложных задач. Класс сложности APX состоит из NP-задач, которые можно аппроксимировать за полиномиальное время с постоянным множительным коэффициентом от оптимального решения. Это позволило разработать множество очень полезных приближенных классических алгоритмов для широкого спектра задач комбинаторной оптимизации.
В ряде современных публикаций отмечается, что классические алгоритмы включают эволюционные алгоритмы, жадные алгоритмы, линейное и нелинейное программирование, а также методы штрафов и барьеров, алгоритмы, имеющие дело с другими переформулировками исходной задачи [11, 15]. Согласно еще одной точке зрения традиционные подходы к оптимизации могут быть разделены на следующие группы:
1. Быстрая сортировка – это алгоритм, основанный на принципе «разделяй и властвуй», со средней оценкой времени выполнения
О(NlogN),
где N – количество элементов в массиве. Алгоритм показывает высокую практическую эффективность благодаря малым постоянным множителям, однако в худшем случае его временная сложность составляет
О(N2),
что делает его неэффективным при определенных входных данных.
2. Оптимизация слиянием обладает как средней, так и наихудшей оценкой времени выполнения, обеспечивая стабильную и предсказуемую производительность. Однако данный метод требует дополнительной памяти для временных массивов, используемых при слиянии, что делает его менее эффективным с точки зрения использования памяти по сравнению с быстрой сортировкой.
3. Пирамидальная оптимизация. Это алгоритм оптимизации функционирует на основе сравнений и имеет наихудшую временную сложность. Он особенно полезен в ситуациях, где требуется стабильное поведение в наихудшем случае. Однако на практике этот подход, как правило, уступает быстрой сортировке по скорости из-за более высоких постоянных множителей во временной сложности.
4. Оптимизация вставками – хотя этот алгоритм неэффективен для больших наборов данных, обладая временной сложностью
О(N2)
в худшем случае, она оказывается полезной при работе с почти отсортированными массивами или с небольшими объемами данных.
Описанные выше методы оптимизации представляют собой определенный компромисс между исследованием (то есть склонностью алгоритма к выборке из областей с высокой степенью неопределенности) и эксплуатацией (склонностью к выборке из областей, которые могут предложить улучшение по сравнению с текущим лучшим наблюдением). В то же время в научных кругах на сегодняшний день нет единого мнения о наиболее эффективном подходе к достижению этих целей.
В некоторых публикациях для определения оптимальных параметров ученые предлагают использовать метаэвристические алгоритмы оптимизации. Это включает в себя создание функции затрат, а затем применение алгоритмов оптимизации для ее минимизации, что приводит к определению параметров, которые дают наименьшее значение функции затрат [7, 9, 13].
Рассмотрим некоторые из этих алгоритмов более подробно.
Обобщенный поиск шаблонов (GPS)
GPS, пожалуй, является самым простым и наименее сложным в группе метаэвристических алгоритмов. Это метод прямого поиска, не основанный на вероятностных расчетах и не требующий вычисления градиентов. Ключевым элементом алгоритма GPS является шаблон, с помощью которого алгоритм выделяет набор точек (называемый сеткой), окружающих текущее положение, где цель оценивается на каждом шаге, которая называется фазой опроса.
Детали реализации алгоритма включают в себя следующие шаги.
1. Границы поиска входных параметров линейно масштабируются до интервала [0,100]. Это необходимо, поскольку используемый размер сетки одинаков во всех измерениях.
2. При каждом успешном опросе размер сетки удваивается. И наоборот, после любого неудачного опроса он уменьшается вдвое.
3. Алгоритм останавливается, когда достигается максимальное количество оценок целевой функции.
Метод имитации отжига (SA)
Алгоритмы SA часто используются для поиска глобального минимума в задачах оптимизации, характеризующихся множеством локальных минимумов. Согласно методу SA, значения входных параметров представляют состояние системы, целевая функция действует как функция энергии, а параметр, управляющий процессом оптимизации (отжига), рассматривается как переменная температуры [16].
Для инициализации процедуры случайным образом генерируется начальный вектор входных параметров (начальное состояние системы) и вычисляется его значение приспособленности (цель). Затем с помощью функции соседства выбирается новая пробная точка. Она описывает расстояние новой точки от текущей с масштабом, зависящим от текущей температуры. Наконец, если новая точка более пригодная, чем текущая, она принимается и становится следующей точкой, если новая точка менее пригодная, она принимается с вероятностью, заданной функцией принятия. Эта функция чувствительна к разнице между новым и предыдущим значениями пригодности, а также к параметру температуры.
Рассмотреть все классические алгоритмы оптимизации в рамках данной статьи не представляется возможным, поэтому в табл. 1 систематизированы характеристики некоторых из них, обозначены их достоинства и недостатки.
Хотя все классические методы обеспечивают как сходимость, так и завершение, они зачастую подвергаются критике за то, что являются только локально сходящимися. Обычно их прогресс заканчивается при достижении достаточной точности или после прохождения определенного числа итераций. Поскольку крупномасштабные оптимизационные задачи обычно являются невыпуклыми, вероятность априорного нахождения глобального минимума при использовании классических методов ничтожно мала. Классические эвристические методы часто достигают сверхлинейных или даже экспоненциальных скоростей сходимости, но при этом теряют гарантию получения глобального решения.
Таким образом, после изучения особенностей различных классических алгоритмов оптимизации целесообразным является анализ новых парадигм, выходящих за рамки традиционных вычислительных подходов.
Квантовая оптимизация представляет собой принципиально иную структуру для решения комбинаторных и непрерывных оптимизационных задач с использованием принципов квантовой механики [6]. В отличие от классических методов, основанных на итеративных эвристических алгоритмах поиска или математических релаксациях, квантовые алгоритмы используют суперпозицию, запутанность и интерференцию, что позволяет проводить более эффективное исследование пространств решений, особенно для задач, характеризующихся сложными ландшафтами и экспоненциальными пространствами поиска. Для задач оптимизации было разработано несколько квантовых парадигм, использующих различные алгоритмические стратегии и аппаратные реализации. Эти методы охватывают различные приемы, начиная от вариационных квантовых вычислений и до квантового отжига, квантовой оценки фазы, а также адаптации классических алгоритмов к квантовым условиям. Охарактеризуем более подробно некоторые из них.
Таблица 1
Классические алгоритмы оптимизации и их характеристика
|
Алгоритм |
Тип задачи |
Характеристика |
Преимущества |
Ограничения |
|
Градиентный спуск |
Непрерывная, дифференцируемая |
Использует производные для итеративного приближения к минимуму функции |
Прост в реализации, эффективен при хорошей инициализации |
Не работает для недифференцируемых или сильно несимметричных функций |
|
Метод Ньютона |
Непрерывная, дважды дифференцируемая |
Учитывает вторую производную (гессиан) для ускоренной сходимости |
Быстрая сходимость при хорошем приближении |
Вычислительно затратен, чувствителен к начальным условиям |
|
Симплекс-метод (линейное программирование) |
Линейная, ограниченная |
Пошаговый метод перемещения по граням многогранника |
Надежный для задач линейной оптимизации |
Неприменим к задачам с нелинейными ограничениями |
|
Метод имитации отжига |
Дискретная/ комбинаторная |
Стохастический метод, имитирующий термодинамический процесс охлаждения системы |
Может избегать локальных минимумов |
Не гарантирует глобальный минимум, нуждается в подборе параметров |
|
Генетический алгоритм |
Универсальный (дискретный/ непрерывный) |
Эволюционный подход: популяции, скрещивание, мутация |
Гибкость, применим к задачам без четкой структуры |
Медленная сходимость, высокая вычислительная нагрузка |
|
Метод роя частиц |
Непрерывная, многомерная |
Частицы перемещаются в пространстве решений, ориентируясь на лучший опыт группы |
Хорошо работает для сложных нелинейных функций |
Может застревать в локальных минимумах, требует тонкой настройки |
|
Метод стохастического градиента) |
Непрерывная, стохастическая |
Актуален для оптимизации функций потерь в обучении моделей |
Эффективен в задачах машинного обучения с большим объемом данных |
Колебания в сходимости, требует адаптации скорости обучения |
Источник: составлено автором на основе полученных данных в ходе исследования.
Вариационные и кубит-эффективные квантовые алгоритмы
Квантовые вычисления на основе логических вентилей используют схему, в которой квантовые состояния кодируют задачи оптимизации и манипулируются с помощью квантовых вентилей. Ключевым классом алгоритмов в этой парадигме являются вариационные квантовые алгоритмы (VQA), которые переформулируют задачи оптимизации в задачи минимизации энергии. Эти алгоритмы используют параметризованные квантовые схемы, оптимизированные с помощью классических методов [5].
Типичный VQA состоит из двух компонентов: параметризованной квантовой схемы, которая кодирует задачу и генерирует результаты на основе определенных параметров, и классической оптимизационной процедуры, позволяющей итеративно корректировать эти параметры для минимизации результатов квантовой схемы. Комбинируя квантовые схемы с классическими методами оптимизации, VQA используют преимущества обеих вычислительных концепций для более эффективного решения сложных оптимизационных задач. Несмотря на свои ограничения, такие как количество кубитов и частота ошибок, VQA демонстрирует многообещающие результаты на современных квантовых компьютерах эпохи NISQ (шумный квантовый промежуточный масштаб). Исследователи применили VQA к задачам минимизации общего расстояния, продемонстрировав их потенциал для решения реальных оптимизационных задач. По мере совершенствования квантового оборудования ожидается, что квантовые компьютеры NISQ станут ценной платформой для усовершенствования этих гибридных алгоритмов и продвижения к практическим, масштабируемым решениям оптимизационных задач.
Алгоритм приближенной квантовой оптимизации (QAOA)
Этот алгоритм чередует квантовую эволюцию и классическую оптимизацию для решения комбинаторных задач. Было разработано несколько усовершенствований QAOA, в том числе квантовый алгоритм чередующих операторов (QAOAz), который обобщает чередующие операторы для более полного исследования пространства решений.
Таблица 2
Квантовые вычислительные модели для оптимизации
|
Модель / Подход |
Принцип действия |
Тип задач |
Преимущества |
Ограничения |
|
Квантовый отжиг |
Использует адиабатический переход к состоянию с минимальной энергией гамильтониана |
Дискретная, комбинаторная, NP-трудные |
Подходит для задач минимизации, например, квадратичная безусловная бинарная оптимизация, эффективен на физических устройствах |
Зависит от параметров отжига, не всегда дает глобальный минимум |
|
Квантовая вариационная оптимизация |
Гибридная модель: вариационный алгоритм + классическая оптимизация параметров |
Нелинейная, многомерная, задачи с ограничениями |
Устойчива к шуму, подходит для NISQ-систем, возможна настройка под задачу |
Требует множества запусков и классических вычислений для оценки функции |
|
Алгоритм Гровера |
Амплитудное усиление вероятности нужного решения в неупорядоченном пространстве |
Поиск, перебор |
Теоретическое ускорение в |
Не решает задачу оптимизации напрямую, а ускоряет поиск решения |
|
Квантовая имитация отжига |
Эмуляция процесса классического отжига с использованием суперпозиции и интерференции |
Задачи на графах, маршрутизация, планирование |
Может находить хорошие приближенные решения |
Неэффективна при сильном шуме или недостатке кубитов |
|
Гибридные квантово-классические схемы |
Объединение квантовой обработки и классической оптимизации на разных этапах |
Универсальные задачи оптимизации |
Высокая гибкость, возможность масштабирования |
Требует синхронизации и эффективного распределения задач |
|
Адиабатическая квантовая оптимизация |
Плавное преобразование исходного гамильтониана в целевой |
Функции с минимумом, задачи типа выполнимости булевой формулы |
Теоретическая гарантия нахождения глобального минимума (при идеальных условиях) |
Реализация требует длительного времени эволюции и устойчивых систем |
Источник: составлено автором на основе полученных данных в ходе исследования.
Также внимания заслуживает алгоритм теплого запуска QAOA (WS-QAOA), который использует классическую предварительную обработку для инициализации параметров QAOA, ускоряя сходимость, и Multi-Angle QAOA (MA-QAOA), который вводит независимые вариационные параметры для каждого слоя, улучшая производительность [10].
Гибридный подход позволяет QAOA использовать преимущества квантовых устройств, такие как суперпозиция и запутанность, опираясь на классические методы оптимизации для уточнения результатов.
В табл. 2 дана краткая характеристика квантовым алгоритмам оптимизации.
Предполагаемое квантовое преимущество зависит от многих параметров, таких как структура входного экземпляра задачи и допустимые уровни ошибок. Поэтому очень важно проводить тестирование квантовых алгоритмов повторно и абстрактно (то есть статистически усреднять их) на основе массовых повторений. Основные детерминированные алгоритмы со сложным полиномиальным временем в шумной среде должны работать лучше, чем вариационные алгоритмы.
Обобщая результаты проведенного исследования, в табл. 3 представлена сравнительная характеристика классических и квантовых алгоритмов оптимизации в разрезе различных критериев.
Для выбора наиболее эффективного алгоритма оптимизации учеными проводятся многочисленные опыты и эксперименты. В частности, решаются задачи, которые не только являются NP-трудными, но и представляют собой сложность в поиске оптимального или даже возможного решения в разумные сроки. Некоторые задачи сложны из-за сложности достижения оптимальности, другие – из-за того, что многие потенциальные решения являются невыполнимыми. Кроме того, эти задачи охватывают различные цели, включая определение выполнимости, минимизацию и максимизацию [1, 6, 12].
Опираясь на проведенные отечественными и зарубежными учеными исследования, на рисунке изображены результаты использования различных алгоритмов оптимизации.
Таблица 3
Сравнительный анализ классических и квантовых алгоритмов оптимизации
|
Критерий сравнения |
Классические алгоритмы оптимизации |
Квантовые алгоритмы оптимизации |
|
Классы решаемых задач |
Линейные, нелинейные, дискретные, стохастические, многокритериальные задачи |
Дискретные задачи выбора, задачи на графах, задачи булевой оптимизации, задачи комбинаторики |
|
Оценка времени решения |
Полиномиальная или экспоненциальная сложность в зависимости от структуры задачи и используемого метода |
Возможное квадратичное или адиабатическое ускорение при определенных условиях реализации |
|
Пример времени выполнения |
Оптимизация булевой функции (100 переменных): менее 1 с на традиционном процессоре |
Решение аналогичной задачи на квантовом устройстве: от 10 до 20 с |
|
Точность и качество решения |
Высокая точность при использовании методов точной оптимизации, приближенная – при эвристических подходах |
В большинстве случаев – приближенные решения, иногда превосходящие классические эвристики |
|
Требуемые вычислительные ресурсы |
Центральный процессор, оперативная память |
Квантовые разряды, схемная глубина, стабильность квантовых вентилей |
|
Устойчивость к внешним факторам |
Не зависит от физических шумов и квантовых эффектов |
Значительно зависит от уровня декогеренции и технической реализации квантовой аппаратуры |
|
Технологическая доступность |
Повсеместно доступна, включая открытое программное обеспечение и промышленные решатели |
Ограничена – требуется доступ к квантовым вычислительным системам (прототипам или облачным платформам) |
|
Возможность масштабирования |
Хорошо масштабируется при наличии достаточных вычислительных мощностей |
Ограничена числом доступных квантовых разрядов и устойчивостью квантовой схемы |
|
Основные преимущества |
Высокая предсказуемость, проверенная теория, зрелая инструментальная база |
Потенциальное ускорение при решении вычислительно трудных задач, новая парадигма обработки данных |
|
Основные ограничения |
Приближенные методы не гарантируют глобального оптимума; экспоненциальные затраты в сложных задачах |
Низкая надежность текущих квантовых систем, необходимость гибридных моделей |
|
Типичные области применения |
Управление логистикой, финансовое моделирование, обучение нейросетей, планирование ресурсов |
Оптимизация маршрутов, портфельное инвестирование, задачи раскладки, интеллектуальное планирование |
Источник: составлено автором на основе полученных данных в ходе исследования.
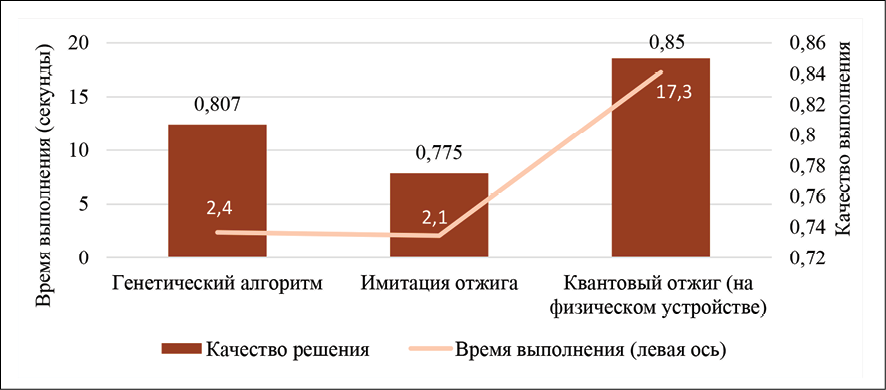
Сравнение эффективности алгоритмов оптимизации Источник: составлено автором на основе полученных данных в ходе исследования
Рисунок демонстрирует эффективность трех подходов к решению задачи максимального разреза графа. Критериями сравнения являются следующие:
1. Качество решения: отражает, насколько близко полученный результат находится к оптимальному (в шкале от 0 до 1).
2. Время выполнения: фактическое время работы алгоритма в секундах.
Согласно приведенным данным, можно отметить, что квантовый отжиг обеспечивает наилучшее качество решения (0,857), но требует значительно больше времени (17,6 с). Имитация отжига – это самый быстрый, но менее точный алгоритм (0,77). В свою очередь, генетический алгоритм является альтернативным по обоим показателям. На основании этой информации можно сделать вывод, что квантовые вычислительные модели способны обеспечивать лучшие результаты по качеству, но пока уступают по скорости и доступности.
Заключение
В данном исследовании освещаются перспективы и ограничения методов квантовой оптимизации по сравнению с классическими подходами.
Квантовые вычисления и их прогнозируемая эффективность по сравнению с традиционными алгоритмами демонстрируют значительный потенциал для решения оптимизационных задач с экспоненциальной сложностью в полиномиальном времени. Кроме того, квантовые алгоритмы способны решить проблему преодоления локальных минимумов путем интеграции классических эвристических методов в процесс. Их основное преимущество заключается в улучшенной сходимости по сравнению со стандартными подходами. Однако время работы традиционных алгоритмов значительно быстрее. Также они остаются эффективными для многих приложений и демонстрируют стабильно хорошие результаты в широком спектре конфигураций.
Таким образом, имеющиеся на сегодняшний день результаты испытаний подчеркивают потенциал квантовых вычислительных процедур в революционном преобразовании процессов решения оптимизационных задач. Но в то же время на данный момент необходимо решить такие проблемы их практического использования, как высокая стоимость материалов для чипов, шумы в цепях и ограниченное количество кубитов.
Конфликт интересов
Благодарности
Библиографическая ссылка
Тырышкин С.Ю. СРАВНИТЕЛЬНЫЙ АНАЛИЗ АЛГОРИТМОВ ОПТИМИЗАЦИИ В КОНТЕКСТЕ КЛАССИЧЕСКИХ И КВАНТОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МОДЕЛЕЙ // Современные наукоемкие технологии. 2025. № 9. С. 144-151;URL: https://top-technologies.ru/ru/article/view?id=40499 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/snt.40499




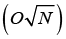 , полезен в NP-задачах
, полезен в NP-задачах