Введение
Интенсивность входного потока представляет собой ключевую характеристику любой системы массового обслуживания (СМО), определяя количество заявок, поступающих в систему за единицу времени, и формируя тем самым ее нагрузку. В классических подходах к моделированию СМО традиционно предполагается стационарность входного потока, когда его интенсивность остается постоянной во времени (λ = const). Такое допущение действительно для многих процессов на ограниченных временных интервалах – например, для производственных линий [1] в течение рабочей смены. Однако в более широком временном контексте большинство реальных систем демонстрирует выраженную нестационарность поведения, обусловленную влиянием внешних факторов: сезонными колебаниями спроса, изменением деловой активности, человеческим фактором и другими динамическими процессами.
Современные исследования [2–4] все чаще обращаются к моделям СМО с нестационарными потоками, где интенсивность поступления заявок является функцией времени λ(t). Подобные модели находят широкое применение при проектировании и анализе: телекоммуникационных сетей (суточные колебания трафика), транспортных систем (пассажиропоток в метро), медицинских учреждений (сезонность обращений), логистических центров (предпраздничный рост заказов), производственных процессов (изменение спроса на продукцию).
Особый практический интерес представляют системы, сочетающие два важных свойства:
1) нестационарный характер входного потока;
2) неоднородность и многофазность обслуживающих приборов по производительности.
В данной работе для моделирования нестационарного потока использовались реальные данные о запросах к серверам Wikipedia за 16 апреля 2025 года. Эти данные демонстрируют типичные суточные колебания трафика: минимальная нагрузка составила 428 553 запроса в час (ночные часы), а пиковая – 1 417 977 запросов в час (утренний период активности). Такой подход позволяет более точно оценить эффективность СМО в условиях, приближенных к реальным. Как показывают исследования [5-7], различие в скорости обработки заявок между приборами может существенно влиять на эффективность системы в целом. При этом оптимальное распределение производительности приборов обслуживания позволяет улучшить ключевые показатели эффективности СМО. Однако большинство существующих работ рассматривает либо нестационарные потоки в однородных системах, либо стационарные потоки в системах с разнородными приборами [8-10].
Настоящее исследование направлено на восполнение этого пробела путем комплексного анализа многофазных СМО, функционирующих в условиях:
- динамически изменяющегося входного потока;
- существенной разницы в производительности обслуживающих приборов;
- необходимости оптимального распределения заявок между фазами.
Цель работы – выявление оптимальных соотношений между нагрузкой на систему и соотношением производительностей приборов в многофазных СМО, обеспечивающих максимизацию пропускной способности системы и минимизацию вероятности отказов. Полученные результаты могут иметь важное прикладное значение для проектирования адаптивных систем обслуживания в различных отраслях экономики.
Материалы и методы исследования
Аналитическое исследование многофазных систем массового обслуживания с нестационарным входным потоком и приборами различной производительности представляет значительные математические сложности. Для таких СМО не существует точных аналитических решений в явном виде, что обусловлено: нелинейностью дифференциальных уравнений Колмогорова [1]; зависимостью параметров от времени; сложным взаимодействием разнородных обслуживающих приборов [10-12].
В связи с этим в 2025 году на базе Казанского национального исследовательского технологического университета был проведен комплекс имитационных экспериментов с использованием программного комплекса AnyLogic. Данная среда обладает рядом ключевых преимуществ: поддержка дискретно-событийного подхода; возможность задания нестационарных параметров; гибкая настройка логики обслуживания; встроенные средства сбора статистики; визуализация процессов в реальном времени. На рисунке 1 представлена модель многофазной СМО, состоящая из стандартных объектов среды AnyLogic [12].
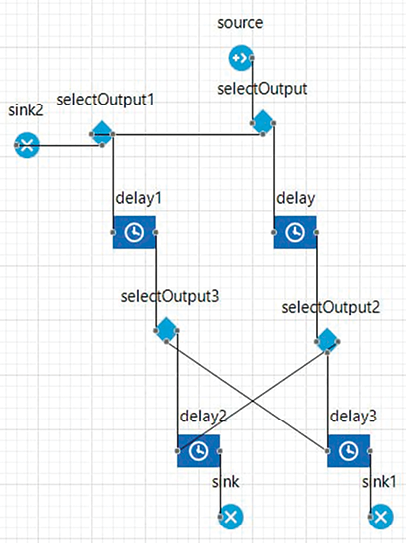
Рис. 1. Модель многофазной СМО Примечание: составлено авторами по результатам моделирования
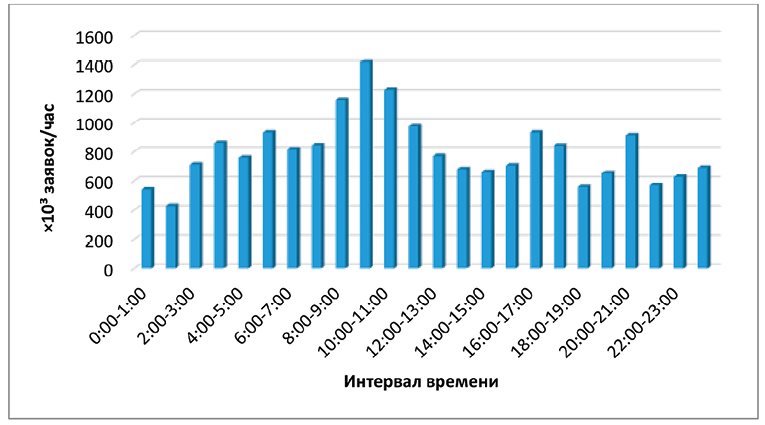
Рис. 2. Гистограмма распределения интенсивности входного потока (×10³ заявок/час) Примечание: составлено авторами на основе данных о часовой нагрузке серверов Wikipedia за 16 апреля 2025 года
Конфигурации многофазной СМО с распределением производительности приборов (μ₁, μ₂, μ₃, μ₄)
|
μ₁ |
μ2 |
μ3 |
μ4 |
||
|
Приборы одинаковой производительности |
СМО-0 |
500 |
500 |
700 |
700 |
|
Приборы различной производительности |
СМО-1 |
450 |
550 |
650 |
750 |
|
СМО-2 |
400 |
600 |
600 |
800 |
|
|
СМО-3 |
350 |
650 |
550 |
850 |
|
|
СМО-4 |
300 |
700 |
450 |
950 |
|
|
СМО-5 |
200 |
800 |
400 |
1000 |
|
|
СМО-6 |
150 |
850 |
350 |
1050 |
|
|
СМО-7 |
100 |
900 |
250 |
1150 |
|
|
СМО-8 |
50 |
950 |
100 |
1300 |
Примечание: составлено авторами по результатам вычислительных экспериментов.
В качестве основы для моделирования нестационарного потока использовались реальные данные о нагрузке на серверы Wikipedia за 16 апреля 2025 года [13]. Расписание интенсивности входного потока представлено на рисунке 2.
Таким образом, в исследуемой системе интенсивность входного потока изменяется в течение суток в диапазоне от 428,553 до 1417,977 заявок в час. Подобное поведение характерно для многих реальных систем, таких как серверные кластеры крупных интернет-ресурсов (на примере Wikipedia) или высоконагруженные call-центры [14; 15]. С разработанной моделью проведена серия вычислительных экспериментов, направленных на сравнительный анализ эффективности многофазных СМО с различными распределениями производительностей обслуживающих приборов. В качестве ключевых показателей эффективности были выбраны: P₀ – вероятность свободного состояния системы и Pотк – вероятность отказа в обслуживании.
Для однозначности сравнения введены следующие обозначения:
- P₀₁ и Pотк₁ – показатели для базовой конфигурации (СМО-0) с приборами одинаковой производительности;
- P₀₂ и Pотк₂ – показатели для тестируемых конфигураций (СМО-1...СМО-8) с различной производительностью приборов.
При моделировании работы систем с неоднородными приборами применялся алгоритм динамического распределения нагрузки, согласно которому входящие заявки направляются на свободный прибор с максимальной производительностью. Данный подход доказал свою эффективность в предыдущих исследованиях для систем без очереди.
Результаты исследования и их обсуждение
Проведенные вычислительные эксперименты охватывали анализ девяти различных конфигураций многофазных СМО, характеристики которых представлены в таблице.
Каждая конфигурация отличается уникальным распределением производительностей обслуживающих приборов при сохранении постоянной суммарной мощности системы.
Результаты анализа вероятности свободного состояния (P₀)
Для оценки влияния неоднородности производительности приборов на эффективность системы был проведен сравнительный анализ изменения вероятности свободного состояния P₀ относительно базовой конфигурации (СМО-0). Результаты представлены на рисунке 3.
Методика расчета
Для каждой конфигурации (от СМО-1 до СМО-8) вычислялось отклонение по формуле:
ΔP₀ = P₀_i – P₀_0,
где P₀_0 = 0,341 (базовое значение для СМО-0).
Полученные значения были визуализированы в виде столбчатой диаграммы. На оси X отображены номера конфигураций (СМО-1 – СМО-8), а на оси Y – значения ΔP₀. Для наглядности использовано цветовое разделение: зеленый обозначает положительные значения, а красный – отрицательные.
Ключевые результаты (рис. 2)
Наибольшая положительная эффективность (ΔP₀ > 0) наблюдается в конфигурациях СМО-1 – СМО-4, где диспропорция составляет 10–40%. Максимальный прирост достигнут в СМО-2 и составляет +0,024.
Переходная зона включает СМО-4 с ΔP₀ = +0,020 и СМО-5, где отклонение становится отрицательным (ΔP₀ = -0,013).
При дальнейшем увеличении диспропорции (более 50%) наблюдается резкое снижение эффективности. Наихудший результат зафиксирован в СМО-8 с минимальным значением ΔP₀ = -0,186.
Результаты анализа вероятности отказа (Pотк)
На рисунке 4 представлены результаты сравнительного анализа изменения вероятности отказа для различных конфигураций системы. График отражает зависимость ΔPотк от степени неоднородности производительности приборов.
Методика расчета
Для каждой конфигурации определялось отклонение по формуле:
ΔPотк=Pотк_0-Pотк_i,
где Pотк_0 = 0,226 (базовое значение для СМО-0).
Результаты были визуализированы на диаграмме, где по оси X указаны номера конфигураций (СМО-1 – СМО-8), а по оси Y – значения ΔPотк. Положительные значения выделены синим цветом, а отрицательные – оранжевым.
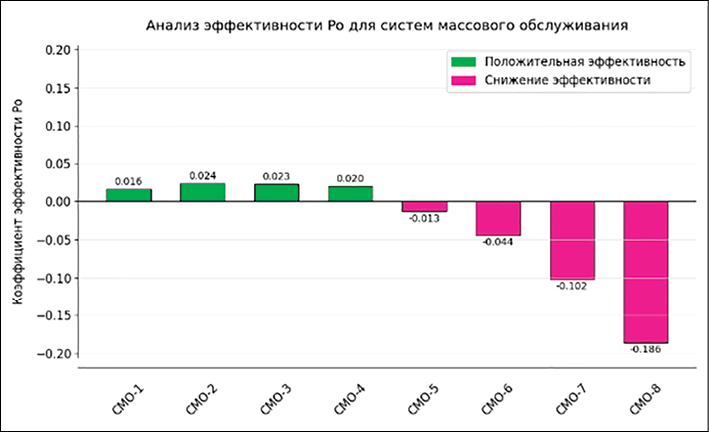
Рис. 3. Зависимость изменения вероятности свободного состояния (ΔP₀) от степени неоднородности производительности приборов в многофазной СМО Примечание: составлено авторами по результатам данного исследования
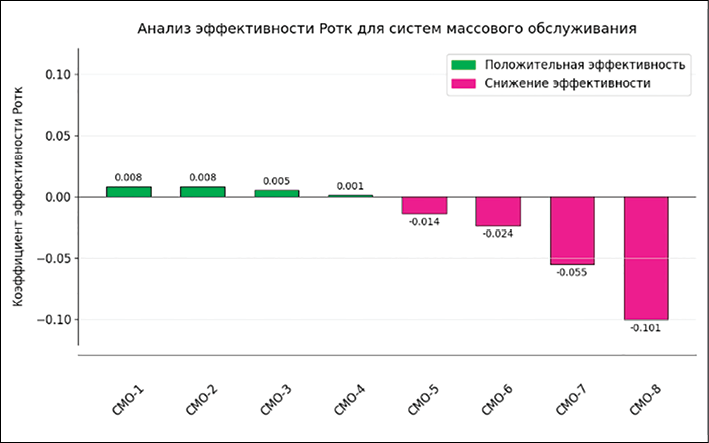
Рис. 4. Зависимость изменения вероятности отказа (ΔPотк) от степени неоднородности производительности приборов Примечание: составлено авторами по результатам данного исследования
Выводы
Проведенное исследование многофазных систем массового обслуживания с нестационарным входным потоком и приборами различной производительности позволило сделать следующие ключевые выводы.
Оптимальная конфигурация
Умеренная неоднородность производительности приборов (20-30%) демонстрирует максимальную эффективность. Для исследованных параметров наилучшие показатели достигнуты в конфигурациях СМО-2 и СМО-3, где наблюдается увеличение вероятности нулевой очереди (P₀) на 4.7-7.0% и снижение вероятности отказа (Pотк) на 3.5-5.2%.
Критические ограничения
Диспропорция производительности свыше 50% приводит к резкому ухудшению характеристик системы: снижению P₀ до 18.6% и росту вероятности отказа до 10.1%. В таких условиях формируются «узкие места» в фазах с минимальной производительностью, что негативно влияет на общую эффективность системы.
Практические рекомендации
Для систем с нестационарной нагрузкой рекомендуется обеспечивать адаптивное распределение нагрузки и избегать экстремальных диспропорций в производительностях устройств. Оптимальная суммарная производительность системы должна на 15-20% превышать пиковую нагрузку для обеспечения устойчивой работы.
Практическая ценность
Полученные результаты имеют важное значение для проектирования IT-инфраструктуры (серверные кластеры, облачные системы), производственных и логистических комплексов, телекоммуникационных сетей нового поколения, а также систем обработки данных в реальном времени.
Исследование подтвердило гипотезу о существовании оптимального уровня неоднородности производительности приборов, обеспечивающего максимальную эффективность многофазных СМО в условиях нестационарных нагрузок.
Конфликт интересов
Библиографическая ссылка
Габдрахманов Б.М., Самерханов И.З., Нуриев Н.К. ВЛИЯНИЕ НЕСТАЦИОНАРНОГО ПОТОКА НА ЭФФЕКТИВНОСТЬ МНОГОФАЗНОЙ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ПРИБОРАМИ РАЗЛИЧНОЙ ПРОИЗВОДИТЕЛЬНОСТИ // Современные наукоемкие технологии. 2025. № 9. С. 45-50;URL: https://top-technologies.ru/ru/article/view?id=40484 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/snt.40484



