Введение
Экзаменационные оценки являются измерителями результатов учебной деятельности. Исследование оценок позволяет выявлять различные недостатки учебного процесса и определять направления его улучшения. Еще одной важной задачей является прогнозирование успеваемости. Прогноз не только позволяет оценить будущее количество обучающихся, но и предложить ряд мероприятий для уменьшения количества неуспевающих.
На экзаменационную оценку влияет большое количество факторов, таких как уровень подготовки обучающегося, личностные характеристики, условия проживания, организация учебного процесса, взаимоотношения с экзаменатором. Многие факторы являются случайными. Все это приводит к тому, что оценку рассматривают как случайную величину, для которой нужно установить закономерности ее формирования.
Анализ данных успеваемости является значительной частью целого направления исследований – интеллектуального анализа образовательных данных (Educational Data Mining) [1; 2]. Цель такого анализа – выявление различных закономерностей, которые помогли бы прогнозировать показатели успеваемости и повышать качество обучения. В основном применяются различные методы математической статистики. В работе Бодрякова В.Ю., Торопова А.П. и Фоминой Н.Г. [3] проведен статистический анализ динамики успеваемости для выявления «проблемных зон качества» образовательного процесса и формирования рекомендаций по его улучшению.
Применение двухфакторного дисперсионного анализа [4; 5] позволяет установить, что оценки разных обучающихся (экзаменов) не принадлежат одной генеральной совокупности. Использование соответствующих средних значений не дает полной характеристики процесса оценивания. Обучающийся характеризуется собственным «смещением» оценки в положительную или отрицательную сторону. Это справедливо и в отношении экзаменов, каждый из которых использует принципы измерения, отличные от применяемых на других экзаменах.
Ряд исследований посвящен регрессионным моделям, оценивающим влияние различных факторов на оценки. Применяются линейные модели [6] на основе ретроспективных данных о показателях обучения в школе и вузе. В работах Галимовой Н.С. и Загитовой Л.Р. [7], а также Лебедевой Т.В., Цыпина А.П. и Сидоренко В.С. [8] используют такие факторы, как баллы ЕГЭ, средний балл аттестата, наличие специального профессионального образования, домашний регион обучающегося, пол, источник финансирования учебной деятельности. В исследовании Канапухина П.А., Коротких В.В. и Щекунских С.С. [9] отмечается отсутствие статистически значимых линейных связей между вступительными баллами и успеваемостью обучающихся. В работе Шафоростовой Е.Н. и Лазаревой Т.И. [10] для прогноза успеваемости предлагается использовать оценки по тестам интеллекта и мотивации. Отмечено влияние перечисленных факторов, но не выявлены линейные связи такого влияния. Кроме классических регрессионных моделей используются нейросетевые модели [11; 12], предсказывающие успеваемость по наблюдаемым оценкам и набору социальных факторов. Все перечисленные исследования отмечают влияние личностных характеристик обучающихся на оценки успеваемости.
В исследовании Егоровой Е.С. и Поповой Н.А. [12] рассматривается неоднородность различных подгрупп студентов и строятся модели классификации этих подгрупп для прогнозирования академических результатов. Исходные данные включают социально-демографические (возраст, пол, социально-экономический статус) и академические данные, собранные во время набора студентов в вуз, а также данные об активности, полученные с помощью электронной информационно-образовательной среды. В работе Сосницкой В.Н. и Потанина Н.И. [13] проверяется наличие функциональной зависимости между средней успеваемостью и вероятностными характеристиками получения каждой из возможных оценок и выдвигается гипотеза о возможном существовании двух психологических характеристик, присущих каждому студенту и определяющих распределение вероятностей его оценок. В данных работах влияние личностных характеристик студента на успеваемость учитывается в виде принадлежности его определенному классу или кластеру.
Среди факторов, влияющих на успеваемость, все чаще рассматриваются характеристики личности, названные в [14] академическими способностями, в которые объединяют когнитивные, психомоторные, коммуникативные, организаторские, волевые способности, для их измерения используются различные психологические тесты.
В анализе данных успеваемости используются в основном характеристики обучающихся. Очевидно, что значительное влияние на оценки оказывают характеристики экзаменатора и технология оценивания знаний. Учет факторов, связанных с экзаменом, должен существенно повысить качество анализа успеваемости. Для более точного описания процесса оценивания знаний модель должна использовать и характеристики обучающихся, и особенности экзаменов.
Цель данной работы заключается в изучении влияния на оценки характеристик обучающихся и особенностей экзаменов. Для этого предлагается использовать модель вероятностного распределения экзаменационной оценки в виде функции Softmax, в определение которой входят латентные параметры, характеризующие уровни подготовленности обучающихся и трудности для каждой градации экзаменационной оценки. Для оценки параметров необходимо построить алгоритм их вычисления по наблюдениям оценок. Адекватность модели должна проверяться статистическими критериями.
Материалы и методы исследования
На экзаменационную оценку влияют, с одной стороны, факторы, связанные с обучающимся, с другой – факторы, связанные с экзаменом, такие как требовательность экзаменатора и сложность вопросов и заданий. Наиболее значимые факторы, такие как академические способности обучающихся, затруднительно измерить непосредственно. Поэтому и факторы обучающихся, и факторы экзаменов предлагается характеризовать латентными переменными. Такой подход давно и успешно применяется в Item Response Theory (IRT) [15, с. 10-18] для обработки данных тестирования. В IRT вероятность
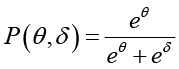
правильного ответа на тестовое задание зависит от «трудности» задания, характеризуемого параметром δ, и уровня «подготовленности» тестируемого, задаваемого параметром θ. Так как эти переменные не наблюдаются непосредственно, то их называют латентными. Вероятность правильного ответа увеличивается при возрастании подготовленности и уменьшается при увеличении трудности.
Оценки обучающихся измеряются в политомической шкале с определенным количеством градаций. В России эта шкала включает следующие градации: «неудовлетворительно», «удовлетворительно», «хорошо» и «отлично». В работе Родионова А.В. [16] для оценки факторов, влияющих на оценки, использовалась Partial Credit Model [17, с. 48-50]. Модель использует латентные параметры трудности для каждой градации оценки, а подготовленность обучающегося описывается одним параметром. Анализ оценок указывает на неравномерность распределения частот для разных градаций, поэтому следует ожидать повышения точности модели при использовании параметра подготовленности для каждой градации оценки.
Для описания вероятностного распределения оценки, измеряемой в политомической шкале, предлагается использовать функцию Softmax [18]. Эта функция широко используется для описания распределений классов, определяемых нейронными сетями. Исходными данными являются наблюдения xij – оценки обучающихся, i – номер обучающегося, j – номер экзамена. Будем считать наблюдения реализациями случайных величин Xij, независимых в совокупности. Для описания соответствующих распределений вероятностей используем функцию Softmax
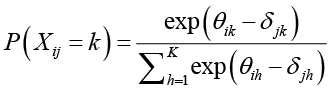 , (1)
, (1)
где k = 1, …, K – номер градации оценки в политомической шкале,
K – количество градаций в шкале,
θik – подготовленность i-го обучающегося добиться k-й оценки,
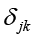 – трудность добиться k-й оценки на j-м экзамене.
– трудность добиться k-й оценки на j-м экзамене.
Введем индикатор Iijk , который равен 1, если xij = k, и 0 – в других случаях. В этих обозначениях
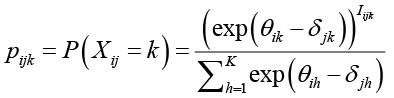 .
.
Логарифм функции максимального правдоподобия
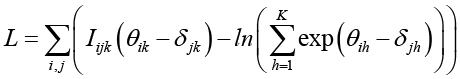
позволяет получить уравнения для вычисления параметров, приравнивая частные производные к нулю
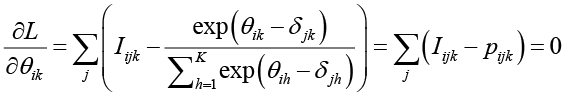 , (2)
, (2)
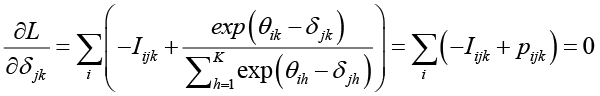 . (3)
. (3)
Пределы суммирования не указаны, так как обучающиеся могут иметь оценки не по всем дисциплинам. Суммирование по i, j подразумевает использование всех оценок, суммирование по i – использование оценок i-го обучающегося, суммирование по j – использование оценок j-го экзамена.
Для итерационного поиска решения таких уравнений в IRT [15, с. 47-50] используется метод касательных
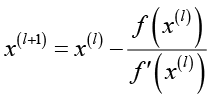 . (4)
. (4)
Для вычислительных процедур в качестве f(x) используются левые части уравнений (2) и (3), а в качестве f′(x) следующие выражения
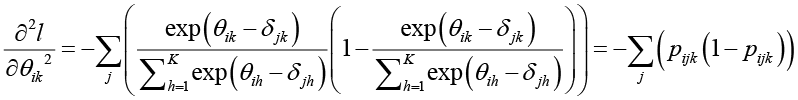 , (5)
, (5)
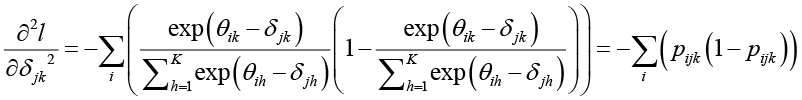 . (6)
. (6)
В предлагаемом подходе смещение всех латентных параметров на одну и ту же величину не изменяет распределение вероятностей. Таким образом, вычислительная процедура сходится к одному набору значений из возможных.
Для определения начальных значений используем выводы работы [19], в которой показано, что при применении байесовского подхода оценка xij = k приводит к увеличению exp(θik) на 1 и к увеличению exp(δjk) на 1 в противоположном случае. Прямое применение байесовского подхода затруднено, так как начальные значения латентных параметров неизвестны и определяются с точностью до некоторого смещения. Возможна ситуация, когда большое количество оценок одного обучающегося приведет к тому, что уровень его подготовленности будет существенно больше уровня подготовленности другого обучающегося с небольшим количеством оценок. Аналогичная ситуация характерна для трудностей оценок экзаменов. Для начальных значений латентных параметров такие неточности байесовского оценивания не играют существенной роли, поэтому положим
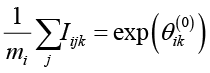 или
или  , (7)
, (7)
где mi – количество оценок i-го обучающегося,
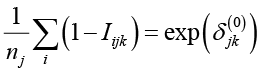 или
или  , (8)
, (8)
где nj – количество оценок j-го экзамена.
Усреднение введено, чтобы компенсировать разницу в количествах оценок у разных студентов (экзаменов).
Особенностью вычислительной процедуры является возможность получения нулевого значения под знаком логарифма или бесконечного роста латентного параметра, если соответствующее значение усредненной суммы равняется единице. Такая ситуация возникает, если все оценки одинаковы или отсутствуют оценки по некоторой градации. В таких случаях латентные параметры ограничивают некоторыми минимальными и максимальными значениями (обычно, предлагается -5 и +5).
Неравенство Рао – Крамера позволяет найти нижние границы дисперсий полученных оценок латентных параметров. Для этого используется информационная матрица Фишера. Для предложенной модели характерно большое количество параметров. Для простоты предположим, что все параметры, кроме θik, известны и совпадают с решением уравнений (2) и (3). В этом случае количество информации Фишера для параметра подготовленности обучающегося
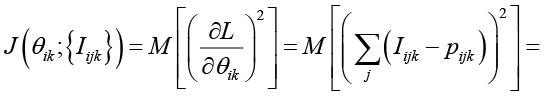
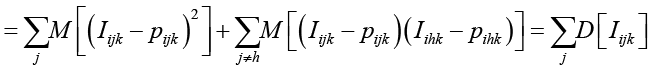
совпадает с суммой дисперсий индикаторов соответствующей оценки, так как вторая сумма математических ожиданий будет равна 0, поскольку индикаторы {Iijk } независимы в совокупности и математическое ожидание произведения будет равно произведению математических ожиданий, каждое из которых равно нулю. Для параметра трудности δjk количество информации будет равно сумме 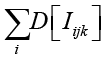 дисперсий индикаторов оценки k на j-м экзамене. Применяя неравенство Рао – Крамера, получаем неравенства
дисперсий индикаторов оценки k на j-м экзамене. Применяя неравенство Рао – Крамера, получаем неравенства
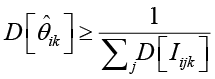 ,
,
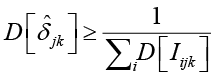 ,
,
которые определяют нижнюю границу дисперсий соответствующих оценок параметров. Для вычисления дисперсий индикаторов 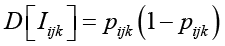 используем оценки вероятностей
используем оценки вероятностей 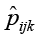 , вычисленные по оценкам латентных параметров. В результате получаем неравенства
, вычисленные по оценкам латентных параметров. В результате получаем неравенства
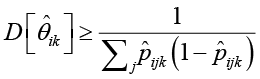 ,
,
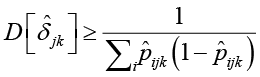 .
.
Неравенства показывают, что с увеличением объема данных дисперсии полученных оценок латентных параметров уменьшаются.
Результаты исследования и их обсуждение
Для проверки адекватности модели обработан набор, включающий 2363 оценки. Изучались оценки для 55 экзаменов 163 студентов одного направления обучения. Обработка данных выполнялась по следующей схеме.
1. Из набора оценок исключались оценки экзаменов и обучающихся, для которых все оценки одинаковы. В таких случаях соответствующие латентные параметры принимают предельные значения (-20 или +20).
2. По формулам (7) и (8) были определены начальные значения латентных параметров.
3. В цикле до достижения требуемой погрешности решения уравнений (2) и (3) вычислялись суммы левых частей этих уравнений, а также производные по формулам (5) и (6). По этим данным методом касательных (4) пересчитывались латентные параметры обучающихся и экзаменов.
4. Определялись статистические характеристики для проверки адекватности модели.
Применялся F-критерий для сравнения внутригрупповых дисперсий
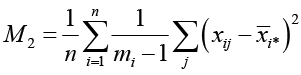 ,
,
n – количество обучающихся, 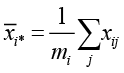 ,
,
с дисперсией всего массива оценок
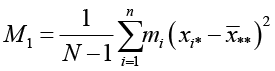 ,
,
N – общее количество оценок, 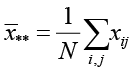 .
.
Если влияние факторов на оценки отсутствует, то M1 и M2 являются разными оценками дисперсии одной и той же случайной величины. Отношение F = M1 / M2 в этих условиях будет иметь распределение Фишера со степенями свободы n – 1 и N – n. Значение F-критерия с уровнем значимости близким к нулю показало несостоятельность этой гипотезы. Такой же результат был получен для групп оценок экзаменов. Это означает, что влияние и обучающихся, и экзаменов на оценки является статистически значимым.
Для проверки того, что предлагаемая модель корректно описывает зависимости законов распределения вероятностей оценок от обучающихся и экзаменов, изучались остатки 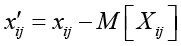 . Математическое ожидание определялось по распределению вероятностей оценки (1), в котором использовались оценки латентных параметров. Гипотезы о принадлежности одной генеральной совокупности остатков оценок и для студентов, и для экзаменов подтвердились с вероятностью близкой к единице. Распределение остатков представлено на рисунке. Гистограмма демонстрирует унимодальность эмпирического распределения. Среднее остатков равно -0,0026. Эмпирическое распределение похоже на распределение Гаусса, хотя эта гипотеза не прошла проверку по критерию хи-квадрат.
. Математическое ожидание определялось по распределению вероятностей оценки (1), в котором использовались оценки латентных параметров. Гипотезы о принадлежности одной генеральной совокупности остатков оценок и для студентов, и для экзаменов подтвердились с вероятностью близкой к единице. Распределение остатков представлено на рисунке. Гистограмма демонстрирует унимодальность эмпирического распределения. Среднее остатков равно -0,0026. Эмпирическое распределение похоже на распределение Гаусса, хотя эта гипотеза не прошла проверку по критерию хи-квадрат.
Исследование зависимостей в явлениях, подверженных случайным воздействиям, требует оценки доли закономерностей, объясняемых моделью, и доли случайных отклонений. В случае с успеваемостью предлагаемая модель определяет закон распределения вероятностей оценки обучающегося на экзамене, в частности математическое ожидание оценки.
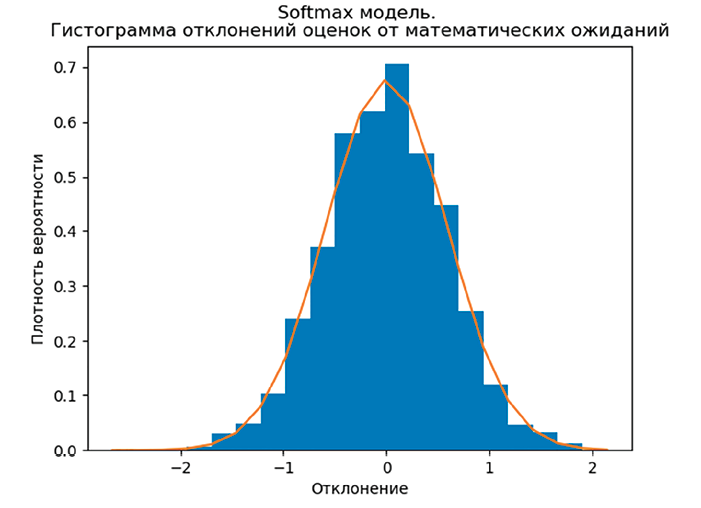
Гистограмма остатков по результатам обработки массива оценок
Насколько точно модель описывает результаты экзаменов, оценивает коэффициент детерминации
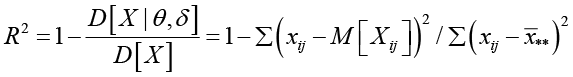 ,
,
который использует сумму квадратов отклонений оценок от соответствующих математических ожиданий. Если бы оценки отклонялись от математического ожидания незначительно, то коэффициент детерминации был бы близок к единице. Однако это не происходит в силу большого количества случайных факторов, влияющих на процедуру оценивания. Для анализируемого списка оценок коэффициент детерминации составил R2 = 0,5916. Это говорит о том, что модель определяет оценку на 59%, а случайное влияние составляет 41%. Вполне возможно, к случайному влиянию будут отнесены закономерности, которые модель не учитывает. Математическое ожидание суммы квадратов отклонений
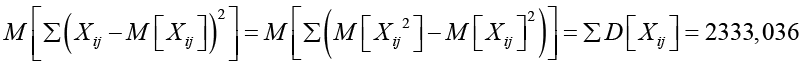
для обработанного набора данных довольно близко к наблюдаемому значению
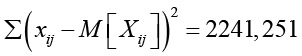 .
.
Это означает, что предложенная модель достаточно точно описывает детерминированную составляющую формирования оценки на экзамене.
Латентные параметры не могут заменить традиционные оценки. Они определяются в процессе итерационных вычислений с точностью до некоторого смещения, одинакового для всех параметров. Латентные параметры подготовленности можно применять для сравнения обучающихся, параметры трудности – для сравнения экзаменов. Сравнение можно применять только в рамках общего массива оценок. Основное назначение латентных параметров заключается в определении законов распределения вероятностей оценок и в прогнозировании успеваемости на этой основе.
Распределения вероятностей экзаменов можно использовать для сопоставления шкал оценивания разных экзаменов [20]. На этой основе возможно введение некоторой стандартной шкалы с усредненными значениями латентных параметров. Применение такой шкалы позволило бы пересчитывать оценки, полученные на разных экзаменах, к оценкам в стандартной шкале и получать, таким образом, более точную картину успеваемости, в частности корректировать результаты экзаменов с завышенными или заниженными оценками.
Заключение
В работе предложена новая модель, которая описывает законы распределения вероятностей экзаменационных оценок в виде функции softmax с латентными параметрами подготовленности обучающихся и трудностей экзаменов. Модель отличается от аналогов [16; 17] применением функции softmax и использованием параметров для каждой градации оценок. Разработаны численные методы определения латентных параметров по набору оценок и методика проверки адекватности модели. Обработка репрезентативного набора оценок авторской программой продемонстрировала возможность применения предложенной модели для решения практических задач.
Преимуществом предложенной модели является более точное описание вероятностного распределения оценок. Практическое применение модели заключается в определении прогнозов оценок и показателей успеваемости по оценкам латентных параметров. Законы распределения оценок можно использовать для выявления экзаменов со значительными отклонениями вероятностей от средних значений для улучшения технологии оценивания.
Конфликт интересов
Библиографическая ссылка
Братищенко В.В. МОДЕЛЬ ЭКЗАМЕНАЦИОННЫХ ОЦЕНОК С ЛАТЕНТНЫМИ ПАРАМЕТРАМИ НА БАЗЕ ФУНКЦИИ SOFTMAX // Современные наукоемкие технологии. 2025. № 9. С. 22-28;URL: https://top-technologies.ru/ru/article/view?id=40481 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/snt.40481



