Актуальность данной работы обусловлена тем, что в настоящее время мы наблюдаем проникновение цифровых технологий во все сферы жизнедеятельности. Не обошла эта участь и образование. Разработаны и приобрели правовую основу такие программы, как «Развитие образования» на 2018–2025 гг., основной целью которой служит достижение высокого качества обучения с применением дистанционных технологий; «Цифровая экономика Российской Федерации», согласно которой до 2024 г. планируется создание современной цифровой образовательной среды, благодаря которой будет обеспечена доступность образования.
Для достижения поставленных целей необходимо в первую очередь обеспечить образовательные учреждения высокоскоростным интернетом, материально-технической базой. К сожалению, по многим объективным и субъективным причинам создание такой цифровой образовательной среды происходит неравномерно. Тем не менее становится актуальным использование доступных цифровых технологий, которые будут способствовать повышению качества обученности, а также формированию и развитию познавательного интереса и мотивации обучающихся. К таким относятся: обучающие компьютерные программы, малые средства информационных технологий, интернет-ресурсы, электронные учебные пособия, учебники и др.
Для нашего исследования интерес представляют малые системы информационных технологий, а именно графические калькуляторы Desmos.
В этой связи целью работы является разработка технологии организации обучения с помощью графического онлайн-калькулятора Desmos при изучении функциональной линии в основной школе.
Материалы и методы исследования
Методами исследования послужили теоретический анализ научной, педагогической и методической литературы, педагогическое наблюдение, опрос, анализ.
Результаты исследования и их обсуждение
Вопросам методики обучения с использованием малых средств информационных технологий (МСИТ) посвящены работы А.В. Бочкарева [1], И.Е. Вострокнутова [2], И.Н. Семеновой [3], А.А Слепухина [3] и др.
Следует согласиться с А.В. Бочкаревым, который подчеркивает, что «анализ эффективности использования систем мультимедиа и информационно-коммуникационных технологий в педагогической среде требует акцента не на оценке конечного результата, а на условиях реализации процесса обучения в целом, что дает возможность отобразить динамику учебной деятельности» [1, с. 206].
Использование графических калькуляторов и методику их применения в процессе обучения математике рассматривали ученые и методисты В.В. Богун [4], Н.Л. Будахина [5], К.Л. Линецкий [6], Т.Л. Седова [6], Е.И. Смирнов [4], Н.К. Трубочкина [6], А.Н. Тихонов [7] и др.
В своих трудах они отмечают, что применение графических калькуляторов на уроках математики повышает интеллектуальную и творческую активность обучающихся, осуществляет интеграцию различных видов учебной деятельности, способствует разработке и внедрению актуальных методов и средств дистанционного обучения на их основе и т.д.
Благодаря их использованию в ряде тем математики значительно увеличивается эффективность урока за счет количества решаемых задач при изучении учебного материала, при этом выполняется один из дидактических принципов – от простого к сложному, исключаются вычислительные ошибки, наличие которых может помешать объяснению и усвоению основной темы, не связанной с этими вычислениями.
А.Н. Тихонов отмечает: «Применение ИКТ на уроках математики способствует: активизации познавательной деятельности, развитию вариативности мышления, математической логики, направленности мыслительной деятельности учащихся на поиск и исследование» [7, с. 115].
Парадигмой современного образования является не факт получения определенного количества знаний учениками, а построение процесса образования так, чтобы обучающиеся сами познавали новый материал, делали собственные маленькие открытия, получали от этого удовольствие. Достичь цели можно только через учебную деятельность обучающегося под умелым руководством учителя, в функции которого входит научить получать знания и правильно их применять.
Таким образом, в данной статье рассмотрим технологию организации обучения с помощью графического онлайн-калькулятора Desmos, основываясь на деятельностном методе обучения.
Как отмечает В.В. Богун, учитель должен составлять задания для обучающихся с применением графических калькуляторов так, чтобы возникала возможность использовать имеющийся личностный опыт работы для конструирования новых знаний. Это возможно при анализе, отборе и обработке информации из таблиц и готовых графиков функций, в ходе которых возникшие противоречия способствуют рефлексивному размышлению, а это, в свою очередь, приводит к открытию обучающимися личностных знаний, что обеспечивает достижение ими метапредметных результатов образования [4].
При подготовке к урокам математики необходимо учитывать следующие дидактические возможности графического онлайн-калькулятора Desmos:
− источник учебной информации,
− наглядное пособие,
− тренажер,
− средство диагностики и контроля.
Приведем пример фрагмента одного из уроков алгебры в 8 классе по теме «Преобразование графиков функций» с использованием графического онлайн-калькулятора Desmos, по учебнику «Алгебра. 8 класс» (авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов).
Цель урока: Научить обучающихся строить графики функций с использованием параллельного переноса, растяжения, сжатия, симметрии относительно осей координат графиков известных функций, а также определять связь между ними по данному графику.
На уроке используются интерактивные методы обучения: «Мозговой штурм», дискуссия, работа в малых группах.
На этапе открытия новых знаний обучающимся предлагается провести «мозговой штурм» и с помощью графического онлайн-калькулятора Desmos выполнить задания по карточкам:
1. Задание: Выяснить связь между графиками функции у = f(х) и у = af(х), где a –число, не равное нулю.
План выполнения:
1) постройте с помощью калькулятора график функции y = x2, заданием соответствующих коэффициентов;
2) с помощью бегунка меняйте значение коэффициента a: а) при a > 1; б) при 0 < a < 1; в) при a < 0;
3) как меняется график квадратичной функции в зависимости от значения коэффициента a?
На этапе анализа и «открытия нового знания» под руководством учителя и благодаря выполнению данного задания, обучающиеся делают вывод, что: «График функции у = af(х) при a > 1 можно получить из графика функции у = f(х) растяжением от оси x исходного графика в а раз; а при 0 < a < 1 – сжатием к оси х графика функции у = f(х) в 1/a раз; а при a < 0 – с помощью симметрии относительно оси Ох» [8, с. 289].
Аналогично изучается связь между графиками функции у = f(х) и у = f(х) + n, где n – произвольное число. Однако учителю необходимо организовать обсуждение и анализ так, чтобы предоставить больше самостоятельности для обучающихся, чтобы они общими усилиями смогли сделать вывод, что: «График функции у = f(х) + n можно получить из графика функции у = f(х) с помощью сдвига вдоль оси у на n единиц вверх, если n > 0, или на │n│ единиц вниз, если n < 0» [8, с. 291].
Доказательную часть полученного вывода можно обсудить в форме дискуссии, предварительно вспомнив материал геометрии, что при параллельном переносе всякая точка A(x0; y0) переходит в точку B(x0; y0 + n).
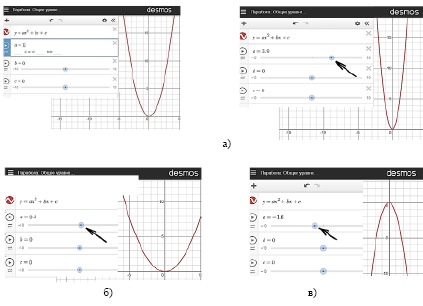
Рис. 1. Динамические модели для анализа роли коэффициента а квадратичной функции
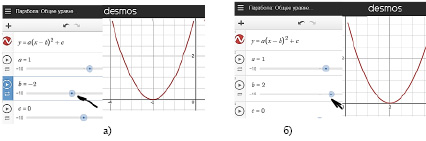
Рис. 2. Динамические модели для анализа роли коэффициента b квадратичной функции
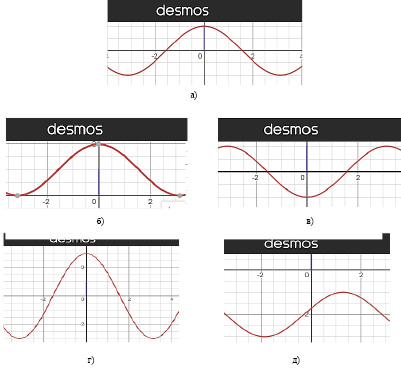
Рис. 3. Задания для этапа рефлексии полученных знаний
Далее, обучающиеся самостоятельно, в малых группах, исследуют с помощью графического онлайн-калькулятора Desmos связь графиков функций у = f(х) и у = f(х – b).
Приходят к выводу, что: «График функции у = f(х – b) можно получить из графика функции у = f(х) с помощью сдвига вдоль оси x на b единиц вправо, если b > 0, или на │b│ единиц вниз, если b < 0» [8, с. 292].
Обобщающим этапом урока является изучение связи между графиками функций у = f(х) и у = f(х – m) + n, где m, n – произвольные числа.
Этот этап урока необходимо провести как самостоятельную работу обучающихся с дальнейшей демонстрацией полученных с помощью графического онлайн-калькулятора Desmos графиков функций у = f(х – m) + n или с проверкой по эталону.
И в конце сформулировать вывод: «График функции у = f(х – m) + n можно получить из графика функции у = f(х) в результате последовательно выполненных двух параллельных переносов: сдвига вдоль оси x на m единиц и сдвига графика функции y = (x – m)2 вдоль оси y на n единиц» [8, с. 292].
После этого уже можно на этапе первичного закрепления новых знаний выполнить номера из учебника.
На этапе рефлексии полученных знаний можно с помощью графического онлайн-калькулятора Desmos заготовить несколько готовых графиков различных функций и попросить обучающихся определить их коэффициенты и, наоборот, по заданным коэффициентам определить соответствие предложенным графикам функций.
Например, задан график функции у = f(х) на рис. 3, а. Установите соответствие между следующими функциями:
1) у = f(х) + 1; 2) у = – f(х);
3) у = f(х+5) – 2; 4) у = 3f(х)
и графиками функций на рисунках б), в), г), д):
Сокращение времени на построение данных графиков, используемая с помощью бегунка анимация позволяют увеличить объем фактически изучаемого материала, высвобождая время для того, чтобы обучающиеся могли:
– выстраивать собственную точку зрения по изменению графика функции в зависимости от ее коэффициентов;
– самостоятельно исследовать, осмысливать и делать выводы по изучаемой теме;
– формировать компетенции по самообучению;
– приобретать новый опыт социализации при работе в группах.
Экспериментальной базой исследования явилась МАОУ «НПСОШ № 2» г. Якутска. В эксперименте приняли участие 142 ученика параллели 8 классов, которых поделили на две группы: экспериментальную, в которой уроки проводились с использованием графического онлайн-калькулятора Desmos, и контрольную, в которой уроки проходили в традиционной форме.
В начале и конце эксперимента были проведены контрольные срезы в обеих группах по теме «Преобразование графиков функций», результаты анализа которых показали, что качество обученности в экспериментальных классах значительно повысилось по сравнению с констатирующим этапом с 45,07% до 59,16%, в то время как в контрольных классах повышение лишь с 43,67% до 46,48 %.
Также проведен опрос обучающихся экспериментального класса, по итогам которого можно отметить, что 95,8% респондентов отметили положительную динамику усвоения изученных тем благодаря использованию графического онлайн-калькулятора Desmos.
Заключение
Анализ полученных данных двух замеров, проведенный опрос и итоги педагогического наблюдения в экспериментальных и контрольных классах свидетельствуют об эффективности разработанной технологии организации обучения с помощью графического онлайн-калькулятора Desmos при изучении функциональной линии в основной школе. В дальнейшем необходимо рассмотреть методику применения малых средств информационных технологий на уроках математики в условиях дистанционного обучения.
Библиографическая ссылка
Эверстова В.Н. ТЕХНОЛОГИЯ ОРГАНИЗАЦИИ ОБУЧЕНИЯ С ПОМОЩЬЮ ГРАФИЧЕСКОГО ОНЛАЙН-КАЛЬКУЛЯТОРА DESMOS ПРИ ИЗУЧЕНИИ ФУНКЦИОНАЛЬНОЙ ЛИНИИ В ОСНОВНОЙ ШКОЛЕ (НА ПРИМЕРЕ ТЕМЫ «ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ФУНКЦИЙ» В 8 КЛАССЕ) // Современные наукоемкие технологии. 2021. № 12-2. С. 337-341;URL: https://top-technologies.ru/ru/article/view?id=38999 (дата обращения: 21.02.2026).
DOI: https://doi.org/10.17513/snt.38999



