Ригидные объекты являются наиболее распространенными в задачах распознавания образов, в частности при поиске данных дистанционного зондирования Земли (ДЗЗ), печатных символов или анализе других устойчивых геометрических фигур. Фундаментальное свойство объектов не менять своей формы при выполнении поворотов и изменении масштаба позволяет упростить задачу их распознавания. Наиболее информативными устойчивыми признаками ригидных объектов являются их контуры, которые фактически служат инвариантами по отношению ко многим преобразованиям [1]. Понятие инварианта в математике и в распознавании образов является важнейшим, поскольку непосредственно связано с задачами классификации объектов различной природы. Системы инвариантов позволяют объединять объекты одного класса и, напротив, разделять объекты, принадлежащие разным классам рассматриваемой совокупности. Выделение контуров является одной из важнейших процедур предобработки изображений в задачах распознавания образов.
Наиболее распространенным способом описания контуров служит цепной код Фримена и его модификации [2]. Контур представляется в дискретном поле (решетке) последовательностью отрезков прямых, квантуемых набором из восьми стандартных направлений от 0 до 7 в окрестности 3х3. Длина вектора определяется наклоном и размером ячейки решетки. Для построения кода фиксируется начальная точка отсчета, затем контур обходится в выбранном направлении и описывается последовательностью цифр. С помощью относительно простых численных методов можно проводить масштабирование, повороты или другие преобразования, необходимые для распознавания. Примером использования кода Фримена для распознавания контуров с применением ЭВМ служит работа [3]. Для распознавания контуров можно применять методы сравнения кодов на основе корреляционных функций, линий положения и инвариантных моментов.
Несмотря на относительную простоту, контур сам по себе представляет специфический графический объект, интересный для специального исследования. К возникающим здесь задачам относятся: выделение контуров из фона; получение компактных инвариантных описаний; сжатие путем перехода от растрового к векторному описанию или приведения к коду, удобному для распознавания. Целью настоящей работы является решение некоторых актуальных задач описания контуров ригидных объектов цепными кодами, сжатия, передачи и распознавания контуров ригидных объектов.
Материалы и методы исследования
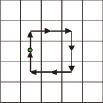
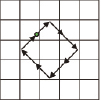
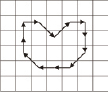
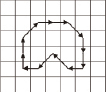
Рассмотрим способы кодирования направлений и их влияние на процессы описания и сравнение контуров. На рис. 1 представлены две модификации системы кодирования направлений, по Фримену [2; 3]. Рассмотрим особенности систем кодирования применительно к следующим простым примерам, представленным в табл. 1. Примеры содержат исходные и повернутые контуры с обходом по часовой стрелке.
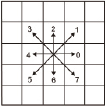
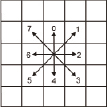
а) кодирование [1] б) кодирование [2]
Рис. 1. Типовые способы кодирования направлений в цепном коде
Таблица 1
Примеры контуров
|
Исходные контуры |
Контуры после поворота |
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
Схемы кодирования, представленные на рис. 1, дают соответственно следующие варианты векторов описаний исходного и повернутого контуров (табл. 2). В рассмотренных случаях сумма всех разностей направлений приводит к нулевому результату, т.к. контур начинается и заканчивается в одной и той же точке.
Таблица 2
Кодирование контуров по Фримену
|
Для кодирования рис. 1, а |
Для кодирования рис. 1, б |
|||
|
Контур |
Кодирование направлений |
Разности направлений |
Кодирование направлений |
Разности направлений |
|
a |
(2,0,0,6,6,4,4,2) |
(0,2,0,-6,0,2,0,2) |
(0,2,2,4,4,6,6,0) |
(0,-2,0,-2,0,-2,0,6) |
|
b |
(1,7,7,5,5,3,3,1) |
(0,-6,0,2,0,2,0,2) |
(1,3, 3, 5,5,7,7,1) |
(0,-2,0,-2,0,-2,0,6) |
|
c |
(2,0,7,1,0,6,6,5,4,4,3,2) |
(0,2,-7,6,1,-6,0,1,1,0,1,1) |
(0,2,3,1,2,4,4,5,6,6,7,0) |
(0,-2,-1,2,-1,-2,0,-1,-1,0,-1, 7) |
|
d |
(2,1,0,0,7,6,6,4,3,5,4,2) |
(0,1,1,0,-7,1,0,2,1,-2,1,2) |
(0,1,2,2,3,4,4,6,7,5,6,0) |
(0,-1,-1,0,-1,-1,0,-2,-1,2,-1, 6) |
Кодирование с применением комплексных чисел рассмотрено в работах [4; 5]. Вектор контура представляется комплексным числом Δx + iΔy, где Δx – смещение точки по оси X, а Δy – смещение по оси Y. Таким образом, контур определяется совокупностью элементарных векторов. Знание размера вектора позволяет восстановить координаты концов. Принцип цепного кодирования представлен на рис. 2. В перечисленных методах кодирование зависит от начальной точки и неустойчиво к зашумлению.
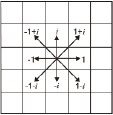
Рис. 2. Комплекснозначное кодирование
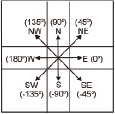
Рис. 3. Кодирование углами
Одной из разновидностей цепного кода является кодирование углами векторов, как это показано на рис. 3 [6]. В табл. 3 представлены примеры построения цепных кодов с применением кодирования углами.
Таблица 3
Кодирование контуров углами и их разностями
|
Контур |
Кодирование углами |
Разности углов |
|
a |
(90, 0, 0, -90, -90, 180, 180, 90) |
(0, 90, 0, 90, 0, -270, 0, 90) |
|
b |
(45, -45, -45, -135, -135, 135, 135, 45) |
(0, 90, 0, 90, 0, -270, 0, 90). |
|
c |
(90, 0, -45, 45, 0, -90, -90, -135, 180, 180, 135, 90) |
(0, 90, 45, -90, 45, 90, 0, 45, -315, 0, 45, 45) |
|
d |
(90, 45, 0, 0, -45, -90, -90, 180, 135, -135, 180, 90) |
(0, 45, 45, 0, 45, 45, 0, -270, 45, 270, -315, 90) |
Смещение начала отсчета приводит к циклическому сдвигу элементов описания, что затрудняет непосредственное сравнение контуров и приводит к необходимости дополнительного анализа. На основе цепных кодов можно последовательно определить все внутренние углы контура, которые являются инвариантом к масштабированию, повороту и сдвигу.
Для сравнения и распознавания контуров в условиях возможного смещения начала отсчетов предлагаются три подхода: на основе корреляционных и автокорреляционных функций, линий положения (для разворота и совпадения ориентации векторов) и инвариантных моментов (инвариантных ко всей группе аффинных преобразований).
При поворотах, масштабировании и изменении точек отсчета описание контуров цепными кодами в общем случае меняется. В то же время для распознавания путем сравнения контуров объектов важно иметь их инвариантные характеристики.
Метод сравнения контуров, описанных комплекснозначными цепными кодами, приведен в работе [4]. Предлагаемый способ сравнения контуров A и B сводится к построению корреляционной функции следующего вида:
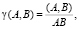
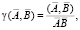
где A, B – описания двух контуров; (A, B) – скалярное произведение, A, B – нормы векторов (описаний контуров). 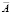 – описание, полученное вычитанием среднего значения из элементов контура. При совпадении контуров имеем максимальное значение γ(A, B) = 1. Однако это возможно только при условии совпадения точек отсчета. Для решения проблемы точки отсчета приходится пользоваться автокорреляционной функцией с параметром циклического сдвига начальной точки. Если A = kB, т.е. векторы контуров, отличаются коэффициентом масштабирования, то
– описание, полученное вычитанием среднего значения из элементов контура. При совпадении контуров имеем максимальное значение γ(A, B) = 1. Однако это возможно только при условии совпадения точек отсчета. Для решения проблемы точки отсчета приходится пользоваться автокорреляционной функцией с параметром циклического сдвига начальной точки. Если A = kB, т.е. векторы контуров, отличаются коэффициентом масштабирования, то 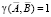

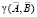
 . Такой подход приводит к построению автокорреляционной функции. Все необходимые пояснения применительно к комплекснозначным векторам – описаниям контуров, приведены в работе
. Такой подход приводит к построению автокорреляционной функции. Все необходимые пояснения применительно к комплекснозначным векторам – описаниям контуров, приведены в работе 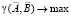 [4].
[4].
Рассмотрим возможности сжатия описаний контуров, представленных цепными кодами. Надо отметить, что эти описания являются достаточно экономичными по объему информации. В общем случае каждое направление по Фримену кодируется тремя битами, что делает цепной код интересным для хранения и передачи данных. Тем не менее для передачи и хранения описаний контуров можно применять методы сжатия и оптимизации. В связи с ограниченным количеством различных направлений векторов и двоичных кодов, описания могут быть эффективно сжаты без потерь с применением стандартных алгоритмов LZW и PCX [7].
С другой стороны, для передачи описаний контуров как сообщений могут быть эффективно применены методы кодирования Хаффмана и Фано [8; 9], учитывающие вероятность (частоту) направлений элементарных векторов. Отсутствие этого учета снижает эффективность передачи описания контура как сообщения. В работе [6] определена вероятность (частота) появления двоичных цифр, представляющих углы поворота в описании контуров цепным кодом Фримена.
Таблица 4
Частота встречаемости углов в цепном коде описания контуров
|
Отклонение угла, в град. |
0 |
±45 |
±90 |
±135 |
±180 |
|
Вероятность (частота встречаемости) |
0.453 |
0.488 |
0.044 |
0.012 |
0.003 |
Из таблицы видно, что самая высокая вероятность (0.488) соответствует углам ±450 и является самой низкой (0.003) для отклонений ±1800 от текущей позиции. Знание вероятностей позволяет оценивать и минимизировать информационную емкость кодирования и передачи цепного кода контура как сообщения. Указанные методы используются для сжатия данных без потерь кодами переменной длины, состоящими из целого количества битов. Символам, появляющимся с большей вероятностью, ставятся в соответствие более короткие коды.
Результаты исследования и их обсуждение
Рассмотрим сообщение (90, 0, -45, 45, 0, -90, -90, -135, 180, 180, 135, 90). Общая цена кодирования по Фримену составляет 36 бит. Упорядочим его элементы в соответствии с табл. 4 (-45, -45, 0, 0, 90, -90, -90, 90, -135, 135, 180, 180). Применяя метод Фано, получим следующую систему кодирования углов (табл. 5).
Таблица 5
Кодирование описания контура по Фано
|
Угол |
±45 |
0 |
90 |
±135 |
±180 |
|
Код |
1 |
01 |
001 |
0001 |
0000 |
С учетом этого общая цена кодирования без учета знака составит 34 бита. Конечно, эффективность кодирования Фано зависит от вида самого контура. В целом же изменение системы кодирования углов оптимизирует описание, уменьшает общую стоимость хранения/передачи графических объектов в виде контуров.
Если восстановить координаты концов векторов в описании контура, то для нормализации его положения можно применить метод линий положения. Метод подробно описан в работе [10]. Две ортогональные линии положения определяют, находя минимум функционала:
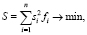
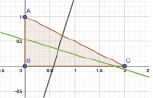
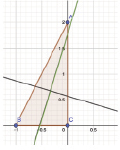
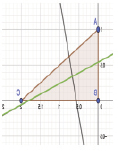
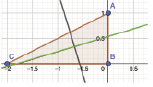
где si – расстояние от точки (xi, yi) с яркостью fi до линии положения объекта, 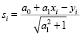 . На рис. 4 показаны примеры построения линий положения для треугольного контура, при fi = 1.
. На рис. 4 показаны примеры построения линий положения для треугольного контура, при fi = 1.
|
|
|
|
|
|
Рис. 4. Линии положения для простого контура
Одна (зеленая) линия является основной. Вторая, вспомогательная линия проходит перпендикулярно главной через центр тяжести контура. Линии положения позволяют вычислить и нормализовать положение контура, т.е. привести его в некоторое стандартное положение. Это позволяет решить проблему начальной точки отсчета и сравнения контуров без перебора.
Рассмотрим возможность применения инвариантных моментов для сжатия и последующего распознавания контуров. Инвариантные моменты для двумерных бинарных и полутоновых изображений описаны в работах [1; 11]. Если восстановить координаты концов векторов, то можно поставить в соответствие контуру алгебраические моменты, инвариантные к аффинным преобразованиям. В табл. 6 приведены результаты кодирования треугольного контура и бинарного изображения буквы.
Таблица 6
Инвариантные моменты
|
Инварианты |
|
|
|
|
|
|
М1 |
1.11111 |
1.11111 |
1.11111 |
2.94954 |
2.94957 |
|
М2 |
0.64197 |
0.64197 |
0.64197 |
7.52499 |
7.52541 |
|
М3 |
0.93278 |
0.93278 |
0.93278 |
10.53995 |
10.54512 |
|
М4 |
0.27435 |
0.2743 |
0.27435 |
10.51106 |
10.50961 |
|
М5 |
0.13740 |
0.13741 |
0.13741 |
21.03661 |
21.03792 |
|
М6 |
0.20972 |
0.20972 |
0.20972 |
14.29213 |
14.29324 |
|
М7 |
-0.01951 |
-0.01951 |
0.01951 |
-22.90534 |
-22.21851 |
Видно, что значения инвариантов практически совпадают. Отличия могут быть вызваны при работе с поворотами реальных изображений, которые вносят искажения. Таким образом, каждому контуру вне зависимости от его сложности, поворота и точки отсчета будет поставлен в однозначное соответствие код из семи действительных чисел – по числу уникальных моментов. Этот код можно использовать для распознавания контуров бинарных и полутоновых изображений любым из известных методов.
Представляет отдельный интерес задача построения инвариантных моментов для одномерного случая описания контуров кодами направлений. Пусть имеется описание контура A = (x1, x2,..., xn), где n – размерность вектора. Так как вторая координата отсутствует, то группа центральных моментов определяется в этом случае по сокращенной формуле:
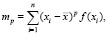
где 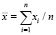 , т.е. все элементарные отрезки контура одной яркости.
, т.е. все элементарные отрезки контура одной яркости.
Тогда группа центральных моментов степени p ≤ 3 примет вид:
m0 = n, 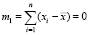 (свойство контура),
(свойство контура), 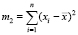 ,
, 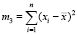 .
.
Далее выпишем значения моментов:
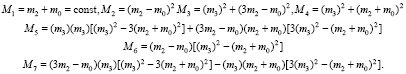
В этом случае метод инвариантных моментов применим для описаний, полученных изменением точки отсчета. В случае нормализации моментов их значения не зависят и от масштабирования векторов. Примеры практического применения метода инвариантных моментов для распознавания образов содержатся в работах [12; 13].
Заключение
Выделение контуров является одной из важнейших процедур обработки изображений. Контур, в общем случае, несет большое количество информации о ригидных объектах и может успешно применяться в задачах их распознавания. В работе рассмотрены различные варианты цепного кодирования контуров по Фримену, показаны алгоритмы, позволяющие выполнять сравнение контуров, в том числе путем корреляционного анализа и линий положения. Рассмотрены вопросы сжатия цепных описаний контуров без потерь на основе кодов Фано для их передачи в виде сообщений. Рассмотренный инструментарий может быть использован при решении задач распознавания целевых объектов по результатам дистанционного зондирования Земли.
Работа выполнена при финансовой поддержке РФФИ (проекты № 20-07-00022-а, № 18-29-03011-мк) и Программы фундаментальных исследований Президиума РАН «Перспективные физико-химические технологии специального назначения» (проект «Разработка и исследование методов и технологии высокопроизводительного сжатия целевой информации, передаваемой по каналам космической связи в интересах национальной безопасности Российской Федерации»).
Библиографическая ссылка
Хачумов М.В. СЖАТИЕ, ПЕРЕДАЧА И РАСПОЗНАВАНИЕ КОНТУРОВ РИГИДНЫХ ОБЪЕКТОВ, ОПИСАННЫХ ЦЕПНЫМИ КОДАМИ // Современные наукоемкие технологии. 2020. № 8. С. 79-85;URL: https://top-technologies.ru/ru/article/view?id=38177 (дата обращения: 05.02.2026).
DOI: https://doi.org/10.17513/snt.38177