Существующие технические системы требуют постоянного развития методологии обеспечения их оптимального функционирования. Наиболее актуальным в энергетике в настоящее время является направление, связанное с организацией цифровых подстанций [1, 2]. Цифровая подстанция, благодаря своей структуре, позволяет концентрировать полную информацию обо всем оборудовании в едином хранилище, что, в свою очередь, дает возможность разработки методов диагностики, нацеленных на комплексную оценку состояния подстанции.
С точки зрения мониторинга параметров раличных процессов в настоящее время активно разрабатываются и применяются компьютеризированные системы [3–5]. В случае, сложных технических систем, компьютеризированные системы оперируют широкой номенклатурой параметров, содержащих скрытую информацию [6–8]. Существенной эффективностью с точки зрения решения задач извлечения скрытой информации обладают комбинированные подходы [9–11]. Совершенствование методов диагностики цифровых подстанций может быть реализовано на базе синтеза двух подходов: натурно-модельного эксперимента и теории диакоптики. Применение теории диакоптики позволяет получить унифицированный подход и модели для диагностики сложных систем различной природы. Использование методологии натурно-модельного эксперимента позволяет наиболее эффективно использовать экспериментальные данные для настройки адекватной модели объекта.
Цель исследования: разработка и исследование алгоритмического и математического обеспечения диагностики сложных систем на базе теории диакоптики и научно-модельного подхода.
Методы и фундаментальные положения
Цифровая подстанция представляет собой совокупность подсистем перетока мощности, измерительной подсистемы, а также подсистемы передачи данных. Соответствующая обобщенная структурная схема представлена на рис. 1. Информационный обмен в системах типа «цифровая подстанция» происходит в соответствии с протоколом передачи данных МЭК-61850. На рис. 1 приняты следующие обозначения: УСО – устройство связи с объектом; ЩПТ – щит постоянного тока; ЩСН – щит собственных нужд; СМ – система мониторинга; РЗА – релейная защита и автоматика; ПА – противоаварийная автоматика; ККЭ – контроль качества электроэнергии; АСКУЭ – автоматизированная система коммерческого учета электроэнергии; РАС – регистрация аварийных событий; ТМ – телемеханика; СМПР – система мониторинга переходных режимов; ОМП – определение мест повреждений; АРМ – автоматизированное рабочее место; ССПТИ – система сбора и передачи технологической информации; ЦУС ФСК – центр управления сетями федеральной сетевой компании.
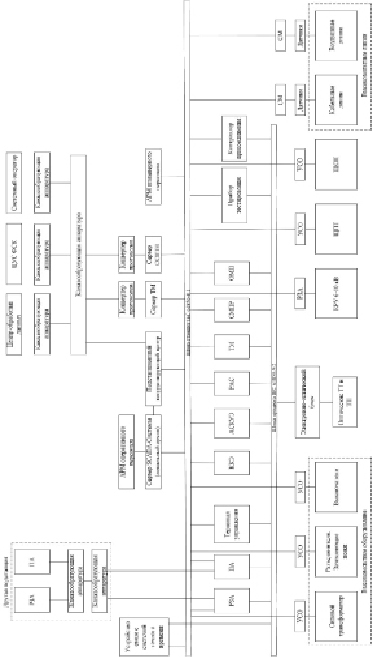
Рис. 1. Обобщенная структурная схема цифровой подстанции
Базовой идеей диакоптики является решение «большой» системы уравнений путем разделения ее на составляющие, соответствующие отдельным подсистемам с последующим комбинированием и синтезом решения исходной системы. Традиционная реализация концепции диакоптики использует теорию тензорного анализа, анализа контуров, топологий и декомпозиции. Для использования методологии тензорного анализа в терминах теории диакоптики требуется предварительное определение модели процессов и соответствующих им подсистем. Понятие «подсистема» в данном случае подразумевает возможность не учитывать наличие других подсистем. Следовательно, эти подсистемы являются независимыми и уравнения, их описывающие, могут быть решены отдельно.
Исходя из базовых положений тензорной [12] методологии сформулированы следующие правила определения величин, характеризующих работоспособность устройств, входящих в моделируемую систему:
1. Перетоки мощности и информации с постоянной интенсивностью λопределяют идентичную загрузку l устройств при изменении структуры системы, т.е.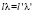 
.
2. Интеграция отдельных систем не вызывает каких-либо изменений в модели, и анализ сложной системы может быть выполнен путем рассмотрения ее подсистемы с последующим применением решения на систему в целом. Таким образом, при рассмотрении подсистем и системы в целом соотношение между интенсивностями их загрузки имеет вид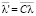 
, где C – матрица перехода.
3. Изменение структуры системы не приводит к изменениям основных соотношений между физическими величинами, описывающими простейший элемент. Иными словами,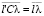 
.
Для дополнения системного представления используется математическое описание связывающих ветвей между подсистемами. Для получения различных компонентов разделенной системы используется следующая система уравнений:
, 
,
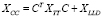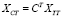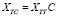, (1)
где XTT – матрица, содержащая информацию обо всех подсистемах, XLLD – диагональная матрица связей, C – матрица контуров, заполненная 1 и 0 для описания соединений между подсистемами.
С учетом системы (1) можно в следующем виде записать общее представление о системе:
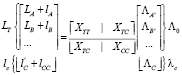. (2)
Используя выражение (2) и систему (1) при рассмотрении процессов перетока мощностей, заменив, можно записать выражение
,
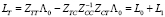в котором левая часть представляет собой решение задачи для подсистемы, а правая – полное решение с учетом ветвей связи. Однако ввиду того, что значения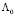 
изменяются во времени, после нахождения этих значений для подсистемы полная модель должна также быть пересчитана.
Для снижения вычислительных затрат предлагается обобщенный алгоритм, в качестве основы которого используются две идеи диакоптики. Согласно первому подходу предполагается, что если система изначально решается относительно некоторых номинальных значений, то затем, без необходимости пересчета всей задачи, может быть получено достаточно точное решение, если какие-то из элементов системы изменяют свое состояние. Математически, рассматривая систему из n уравнений относительно их номинальных значений, можно записать
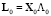, (3)
где X0 – системная матрица,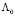 
– вектор состояния системы, L0 – вектор входных воздействий. Предполагается, что m компонентов системы подвергаются отностельно значительным изменениям αi (i = 1…m). В таком случае система уравнений (3) приобретает вид
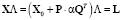, (4)
где X и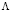 
– новая системная матрица и вектор состояния соответственно; P и Q – матрицы размерностью nxm, содержащие только 0 и ±1 и показывающие размещение изменившихся элементов исходной системы уравнений. Прямой способ решения системы (4) заключается в факторизации матрицы коэффицентов с последующим итерационным подбором вектора X. Однако, если количество элементов, изменивших свое состояние (m), намного меньше, чем размерности системы (n), может быть использовано следующее выражение:
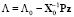, (5)
где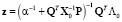 
.
Согласно второму дополнительно используемому подходу для декомпозиции исходной системы используются фиктивные разделители, причем открытое состояние разделителя математически соответствует декомпозиции системы. Данный подход обеспечивает управление распараллеливанием решения всей системы уравнений в целом.
Блок-схема разработанного алгоритма представлена на рис. 2.
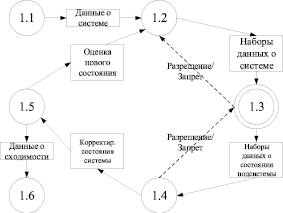
Рис. 2. Алгоритм работы подсистемы моделирования
После первоначального считывания системных данных модулем 1.1 пакеты данных, описывающих отдельные подсистемы, отправляются модулем 1.2 в несколько копий решателей 1.3. Результаты, полученные модулями 1.3, передаются в модуль 1.4, который собирает пакеты результатов, поступающих от отдельных решателей в произвольном порядке, а затем отправляет полный набор результатов для координации в модуль 1.5. Если скоординированные оценки состояния удовлетворяют критерию сходимости, результаты выводятся, в противном случае оценка состояния передается в модуль 1.2 и цикл вычислений повторяется. Программа предназначена для работы в многоядерной системе и может быть использована при кластерной обработке данных. Одной из задач является минимизация потерь на передачу данных и координации одновременного выполнения программных модулей. Рассматривая одну итерацию в цикле моделирования, очевидно, что объем данных, передаваемых между модулями 1.4–1.5 и 1.5–1.2, примерно в n раз больше, чем соответствующие передачи данных между модулями 1.3–1.4 и 1.2–1.3 (где n обозначает количество активных процессоров, выполняющих модуль 1.3). Следовательно, чтобы минимизировать потери, передача данных 1.4–1.5 и 1.5–1.2 была сделана максимально эффективной за счет размещения модулей 1.2, 1.4 и 1.5 (вместе с 1.1 и 1.6) на одном процессоре и использования общего доступа к памяти для неявной передачи данных. Такая возможность доступна, если модули 1.2, 1.4 и 1.5 реализованы в виде потоков, а не задач. Напротив, связь между модулями 1.2–1.3 и 1.3–1.4 включает в себя явную передачу данных, поскольку разные копии 1.3 выполняются на разных ядрах, чтобы максимизировать преимущества, полученные от параллельной структуры алгоритма. Для такой передачи данных потери могут быть минимизированы путем минимизации фактически передаваемых объемов данных. Алгоритм обеспечивает значительное сокращение передаваемых данных между модулями 1.2 и 1.3 путем вычисления якобианов в модуле 1.3 и отправки от 1.3 до 1.4 только тех столбцов обратных якобианов, которые соответствуют конечным узлам разорванных ветвей. Последнее признано значительным улучшением алгоритма диоптики, поскольку оно уменьшает соответствующий трафик данных в 10–100 раз для типичной крупномасштабной системы. В общем случае, число процессоров, доступных для выполнения подсистем 1.3, не равно количеству подсистем, на которые система подразделяется, поэтому кроме прочего необходимо координировать параллельное выполнение потоков отправки и получения. В то время как низкоуровневая синхронизация 1.2–1.3 и 1.3–1.4 обеспечивается в рамках процедур программной среды, прикладная программа должна гарантировать, что никакой решатель 1.3 не останется бездействующим, в то время как некоторые пакеты данных все еще должны быть обработаны. Первоначально процесс решения начинается с отправки пакетов данных всем доступным процессорам. Когда пакет результатов получен 1.4, процесс, который только что завершил выполнение 1.3, становится доступным. Чтобы максимизировать вычислительную эффективность, свободная подсистема получает соответствующие данные и запускается без задержки. Это достигается путем назначения потока, исполняющего модуль 1.2, как «срочного» (с более высоким приоритетом, чем у других потоков) и принудительной отмены планирования потоков каждые несколько миллисекунд.
Реализация и апробация предложенных моделей и алгоритмов
Основываясь на полученных результатах по синтезу моделей для системы диагностики, включая анализ гетерогенной информации, моделирование измерительных устройств с помощью электрических цепей [13, 14], моделирование подсистемы информационного обмена и подсистемы перетоков мощности, разработана модифицированная информационная система диагностики цифровых подстанций на базе технологий National Instruments (NI). В частности, реализация системы диагностики осуществлена в программном пакете NI LabVIEW 2013 при использовании следующих модулей: NI OPC Servers, LabVIEW SignalExpress, NI TimeSync, LabVIEW Electrical Power Suite, LabVIEW Math & Analysis. Интерфейс пользователя разработанной информационной системы представлен на рис. 3.
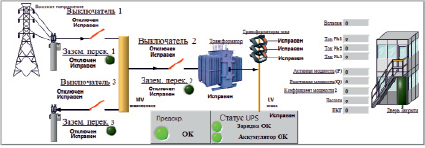
Рис. 3. Интерфейс пользователя информационной системы диагностики цифровых подстанций на базе технологий National Instruments
Предложена адптированная методика оценки адекватности математического обеспечения на базе метода натурно-модельных испытаний [15]. Она характеризуется следующим. Используется единый механизм для экспериментальных проверок адекватности теоретических моделей (в виде совокупности функциональных зависимостей параметров отдельных компонентов) и для диагностики систем путем сравнения высокоточных данных, полученных в разное время. Инструментальную основу методики составляет разработанная в среде графического программирования NI LabVIEW 2013 программа. Суть методики заключается в обеспечении множественного сравнения различных функциональных зависимостей параметров отдельных компонентов. Осуществляется сравнение теоретической и соответствующей ей высокоточно-определенной зависимости, чем обеспечивается возможность мониторинга её состояния. Процесс диагностики включает в себе множество процедур сравнения пар параметров. В каждой паре один из параметров образцовый, а другой – сравниваемый. При сравнении теоретической и высокоточной зависимости или параметра, последняя является образцовой, а теоретическая – сравниваемой. Если сравниваются два экспериментально полученных значения, то образцовой является более ранняя зависимость, а сравниваемой – более поздняя. В каждой паре функциональные зависимости сравниваются в каждой точке аргумента. Критерием оценки адекватности теоретических значений является непревышение максимальным по модулю значением отклонения сравниваемой функциональной зависимости от образцовой заданного допустимого значения. Заключение по результатам сравнений формулируется отдельно.
Для тестов, выполняемых на обычном ПК, аппаратная архитектура состоит из процессора Intel CoreTM i5 2,4 ГГц (2 ядра), 8 ГБ ОЗУ и ОС Windows 7 Professional. В таблице представлены результаты эксперимента по определению максимального количества отключений подсистем, которое может обработать сеть подстанции, не нарушая сквозных требований задержки SV, сообщений отключения GOOSE и состояния GOOSE. Большой сетевой трафик возникает на подстанции, когда происходит чрезмерное отключение и генерируются многочисленные широковещательные сообщения GOOSE (содержащие состояние отключенного автоматического выключателя). Это событие перегружает сеть и может вызвать дополнительные задержки.
Среднее, минимальное, максимальное, отклонение и время задержки стандартного отклонения для сообщений SV в миллисекундах
|
Тип соединения |
Среднее |
Минимальное |
Максимальное |
Отклонение |
Стандартное отклонение |
|
1, Звезда |
0,0432 |
0,0288 |
0,1119 |
0,0001 |
0,0090 |
|
1, Кольцо |
0,0892 |
0,0490 |
0,1801 |
0,0002 |
0,0137 |
|
2, Звезда |
0,0586 |
0,0464 |
0,1214 |
0,0002 |
0,0129 |
|
2, Кольцо |
0,0966 |
0,0464 |
0,2156 |
0,0009 |
0,0296 |
|
3, Звезда |
0,0874 |
0,0464 |
0,2519 |
0,0006 |
0,0244 |
|
3, Кольцо |
0,1421 |
0,0464 |
0,4558 |
0,0036 |
0,0602 |
Выводы
Представлены результаты разработки информационной системы диагностики основных элементов цифровых подстанций. Разработано алгоритмическое и математическое обеспечение информационной системы. Разработана программная реализация предложенных решений в форме информационной системы, реализованной на базе технологий компании National Instruments. Предложена методика оценки адекватности математического обеспечения на базе метода натурно-модельных испытаний. Представлены результаты предварительных исследований. Преимуществом предложенного решения является возможность параллельного решения задачи и повышение оперативности диагностики. Показано, что полученные результаты могут быть использованы для автоматизации мониторинга и диагностики, основанных на средствах имитационного моделирования.
Представленные результаты получены в ходе выполнения проекта РФФИ № 18-38-00950 «Исследование и разработка алгоритмов агрегации гетерогенных данных для развития методов диакоптики и диагностики сложных технических систем на примере цифровых подстанций». Работы были выполнены с использованием оборудования ЦКП ДиЭЭ ЮРГПУ (НПИ).
Библиографическая ссылка
Наракидзе Н.Д. РАЗРАБОТКА И АПРОБАЦИЯ АЛГОРИТМИЧЕСКОГО И МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ ИНФОРМАЦИОННОЙ СИСТЕМЫ ДИАГНОСТИКИ ЦИФРОВЫХ ПОДСТАНЦИЙ НА БАЗЕ ТЕНЗОРНОЙ МЕТОДОЛОГИИ И ТЕХНОЛОГИЙ NATIONAL INSTRUMENTS // Современные наукоемкие технологии. – 2020. – № 8. – С. 57-63;URL: https://top-technologies.ru/ru/article/view?id=38173 (дата обращения: 21.12.2024).