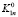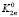В настоящее время при создании программных проектов используется большое количество интегрированных сред разработки приложений, компиляторов и языков программирования. Коллекция компиляторов GNU Compiler Collection (GCC) [1], распространяемая фондом свободного программного обеспечения на условиях лицензий GNU GPL и GNU LGPL, является наиболее доступным и универсальным инструментом генерации исполняемого кода для основных языков программирования: C, C++, Java, Fortran, Ada, Go, D. Отличительной особенностью коллекции компиляторов GCC является поддержка многих операционных систем и аппаратных платформ.
Эффективность генерируемого программного кода, в первую очередь – скорость выполнения проекта, является важнейшей характеристикой языков программирования и компиляторов. Одним из востребованных, универсальных и эффективных языков программирования, в том числе для реализации вычислительных алгоритмов, остается язык C++ [2, 3].
Многие современные компиляторы, в том числе из коллекции GCC, содержат встроенные средства оптимизации исходного кода программы, направленные в том числе на повышение скорости работы приложений. Для объективной оценки влияния различных уровней оптимизации компилятора на повышение эффективности исполняемого кода необходим сравнительный анализ результатов работы нескольких программ, отличающихся алгоритмическими особенностями и протестированных на компьютерах с различными платформами.
Цель исследования в данной работе состоит в получении усредненных оценок повышения эффективности программного кода для различных уровней оптимизации компилятора MinGW-64 GCC [4] при выполнении на трех компьютерах с различной платформой шести тестовых алгоритмов, реализованных на языке С++. Так как время работы программных приложений существенно зависит от используемых базовых действительных типов (одинарная, двойная, расширенная точность), тестирование проводилось для двух основных типов: с двойной точностью (double) и с расширенной точностью (long double). Действительный тип с одинарной точностью (float) не тестировался ввиду того, что в вычислительных задачах применение указанного типа ограничено недостаточно широким диапазоном представления чисел и малой длиной мантиссы.
Материалы и методы исследования
Компилятор для языка программирования C++ из коллекции GCC допускает применение следующих уровней оптимизации, в порядке увеличения скорости работы программы: -O1, -O2, -O3 и -Ofast. Информацию о флагах оптимизации компилятора GCC можно получить с помощью команды man gcc. Конкретный перечень оптимизирующих процедур по каждому из перечисленных уровней оптимизации приведен в [1, 4]. Отметим, что включение опций оптимизации несколько увеличивает время компиляции программ; их использование может оказаться нецелесообразным в проектах, выполняющихся за короткое время.
Результаты ускорения выполнения программ с использованием ключей оптимизации во многом зависят от используемой платформы, поэтому в данном исследовании тестовые расчеты проводились независимо на трех персональных компьютерах с различными характеристиками: ПК1 – IBM PC 32 bit X86 Intel CPU 2.8 ГГц RAM 2 Гб; ПК2 – Note Book 64 bit AMD Phenom(tm) II Quad-Core 2.0 ГГц RAM 4 Гб; ПК3 – IBM PC 64 bit Intel(R) Core(TM) i5-3470 3.2 ГГц RAM 8 Гб.
Введем следующие обозначения. Пусть
i – порядковый номер задачи (1, 2, …, 6);
j – порядковый номер ПК (1, 2, 3);
m – тип данных (1 – double, 2 – long double);
n – уровень оптимизации (0 – без оптимизации; 1 – O1; 2 – O2; 3 – O3; 4 – Ofast).
Тогда tijmn – время выполнения i-й задачи на j-м компьютере для m-го действительного типа данных с n-м уровнем оптимизации компилятора. Для объективности оценки времени выполнения алгоритмов значение параметра tijmn вычислялось как среднее арифметическое из 10 повторных расчетов, после чего фиксировалось время выполнения i-й задачи (в секундах): ti1mn – для первого ПК, ti2mn – для второго, и ti3mn – для третьего.
Очевидно, что средний коэффициент ускорения выполнения i-й задачи на трех ПК может быть вычислен по формуле
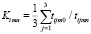; i = 1, 2, …, 6;
m = 1, 2; n = 0, 1, 2, 3, 4, (1)
где tijm0 – время работы алгоритма без оптимизации.
Принятые обозначения использованы в представленных ниже результатах проведенных расчетов. Тестирование проводилось на примерах типичных вычислительных алгоритмов, которые широко встречаются в практике программирования. Все полученные значения приведены с округлением до трех значащих цифр.
Результаты исследования и их обсуждение
Тест-1: итерационный алгоритм. В программе реализован метод последовательных приближений решения краевой задачи для уравнения Пуассона с нелинейными граничными условиями [5, 6]. Особенностью данного алгоритма является отсутствие массивов; задействованы функции пользователя с многократными вызовами; число итераций фиксировано.
Тест-2: сортировка одномерного массива. В качестве теста используется простейший алгоритм обменами (метод пузырька) для упорядочивания одномерного массива c 200000 элементами действительного типа двойной и расширенной точности.
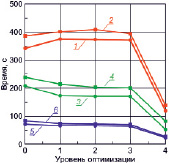
На рис. 1 представлены результаты, полученные в первых двух тестах.
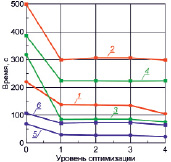
а) б)
Рис. 1. Зависимости времени выполнения программ от уровня оптимизации компилятора в тесте-1 – (а) и в тесте-2 – (б): 1, 2 – ПК1; 3, 4 – ПК2; 5, 6 – ПК3; для базовых действительных типов double – 1, 3, 5 и long double – 2, 4, 6
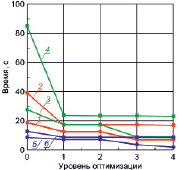
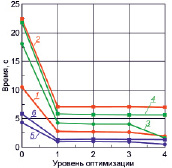
а) б)
Рис. 2. Зависимости времени выполнения программ от уровня оптимизации компилятора в тесте-3 – (а) и в тесте-4 – (б). Остальные обозначения те же, что и в подписи к рис. 1
Как видно из рис. 1, в первом тесте применение оптимизации компилятора с первого по третий уровни не дают заметного эффекта и только при четвертом уровне (-Ofast) среднее время выполнения программы сокращается более чем в 2,5 раза. Для второго алгоритма ситуация кардинально отличается: здесь уже при первом уровне оптимизации значение среднего коэффициента ускорения превышает 2,5 для типа double и достигает 1,7 для типа long double. Включение же второго и третьего уровней оптимизации не приводит к заметным изменениям по сравнению с первым уровнем. Эффект от применения оптимизации четвертого уровня наиболее значителен для типа double (K = 3,1); для типа long double аналогичный показатель гораздо ниже (K = 1,69).
Тест-3: перемножение матриц (вариант А). В данном тесте реализован алгоритм перемножения двух квадратных матриц (1000*1000) c элементами двойной и расширенной точности в его классическом виде «строка – на – столбец».
Тест-4: перемножение матриц (вариант Б). Решается та же задача. Отличие от предыдущего алгоритма заключается в том, что в данном случае учитывается расположение элементов двумерных массивов в оперативной памяти компьютера. Компилятор GCC для языка C++ размещает двумерные массивы в памяти ПК по строкам, поэтому в данном примере для ускорения работы алгоритма транспонируется вторая матрица (строки и столбцы меняются местами), после чего матрицы перемножаются по схеме «строка – на – строку».
На рис. 2 представлены полученные результаты.
Сравнивая результаты данных тестов, отметим, что абсолютное время выполнения задачи по второму алгоритму для всех ПК сократилось в 3–6 раз. Отметим особо результаты вычислений на ПК2 для типа double: при четвертом уровне оптимизации (ключ -Ofast) время выполнения алгоритма сократилось более чем в 11 раз (18,1 с без оптимизации и 1,6 с с четвертым уровнем оптимизации). При максимальном уровне оптимизации средний коэффициент ускорения превышает значение 3,0 для типа double и 2,5 – для типа long double.
Тест-5: метод Гаусса. Численное решение систем линейных алгебраических уравнений (СЛАУ) является актуальной задачей для многих разделов вычислительной математики. Метод исключения Гаусса – один из наиболее известных и часто используемых прямых методов решения СЛАУ [7]. В данном примере тестируется алгоритм решения системы A*x = b методом Гаусса с выбором ведущего элемента по столбцу. Здесь A – матрица (N*N); x и b – векторы из N элементов. Тестирование проводилось для СЛАУ при N = 1400.
Тест-6: метод Гивенса. В данном примере решается та же система линейных алгебраических уравнений, что и в предыдущем тесте, но методом вращений (Гивенса). Метод вращений является наиболее устойчивым к вычислительной погрешности [8, 9], хотя и требует больших усилий при реализации алгоритма.
Результаты полученных расчетов для тестов 5, 6 представлены на рис. 3.
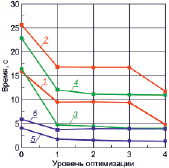
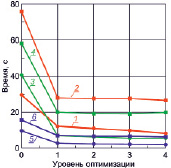
а) б)
Рис. 3. Зависимости времени выполнения программ от уровня оптимизации компилятора в тесте-5 – (а) и в тесте-6 – (б). Остальные обозначения те же, что и в подписи к рис. 1
Сравнивая результаты тестов 5 и 6, приведенные на рис. 3, отметим, что абсолютное время решения СЛАУ методом Гивенса в среднем в 2–2,5 раз больше, чем решение той же задачи методом Гаусса. В тесте 5 при максимальном уровне оптимизации средний коэффициент ускорения оказался равным 3,44 для типа double, и 1,93 – для типа long double; при этом для типа long double уровни оптимизации 1–3 приводят к близким значениям ускорения (1,67–1,70). В тесте 6 средний коэффициент ускорения при четвертом уровне оптимизации достигает значения 5,2 для базового типа double и 2,7 – для типа long double.
Обобщая проведенные исследования, приведем гистограмму распределения коэффициентов ускорений при выполнении шести тестовых алгоритмов с различными уровнями оптимизации компилятора (рис. 4).
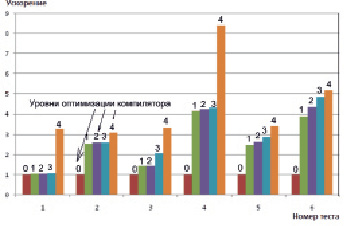
Рис. 4. Коэффициенты ускорения при выполнении программ в шести тестах с выбором ключей оптимизации: 0 – нет оптимизации, 1 – ключ оптимизации -O1, 2 – ключ оптимизации -O2, 3 – ключ оптимизации -O3, 4 – ключ оптимизации -Ofast
По результатам проведенных расчетов получены итоговые оценки на основании соотношения
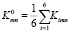; m = 1, 2; n = 0, 1, 2, 3, 4, (2)
которые определяют средние значения коэффициентов ускорения в шести тестовых алгоритмах при различных ключах оптимизации компилятора для двух действительных типов. Результаты, полученные по формуле (2), представлены в таблице
Средние значения ускорений
|
n |
0 |
1 |
2 |
3 |
4 |
|
|
1 |
2,60 |
2,73 |
3,08 |
4,46 |
|
|
1 |
2,20 |
2,21 |
2,22 |
2,60 |
Заключение
Применение средств оптимизации программного кода всех уровней, имеющихся в компиляторе GCC, приводит, как правило, к различному ускорению работы приведенных алгоритмов. Максимальный эффект, как и следовало ожидать, наблюдается при выборе ключа оптимизации четвертого уровня (-Ofast). Наибольшее среднее значение коэффициента ускорения (4,46) получено в алгоритмах с базовым действительным типом double; среднее значение аналогичного показателя для типа long double достигает значения 2,6.
Библиографическая ссылка
Болотнов А.М., Нурисламова Э.А. ВЛИЯНИЕ ОПТИМИЗАЦИИ КОМПИЛЯТОРА GCC НА ЭФФЕКТИВНОСТЬ ПРОГРАММНОГО КОДА В ЯЗЫКЕ C++ // Современные наукоемкие технологии. 2019. № 12-2. С. 266-270;URL: https://top-technologies.ru/ru/article/view?id=37869 (дата обращения: 19.05.2025).
DOI: https://doi.org/10.17513/snt.37869