Рис. 1 - Вид гребного винта с поворачивающимися лопастями
Главные параметры функционирования системы судна представлены в рис. 2.
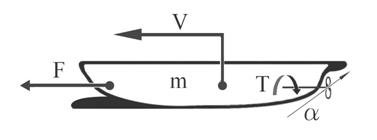
Рис. 2 - Параметры функционирования системы судна
Матричная форма уравнений математической модели имеет вид [1]:
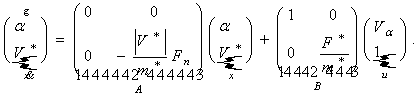(1)
где V - скорость судна, F - движущая сила, m - масса судна, T - вращающий момент двигателя, 
- угол поворота лопастей винта, 
- управление (скорость изменения угла поворота лопастей винта) (градусы в секунду), символ «* » означает измерение в относительных единицах; Vn , Fn обозначают номинальную скорость судна и номинальную движущую силу (при номинальном угле поворота лопастей винта).
Таким образом, математическая модель функционирования водного судна описана системой нелинейных разностных уравнений вида [2]:
где x(k) - вектор, компоненты которого определяют состояние объекта в момент времени k; 
- 2-мерный вектор управляющих воздействий; 
- матрица параметров, 
- матрица влияния управляющих воздействий;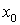 
- вектор состояния в начальный момент времени.
Управляющее воздействие формируется по закону [1,2]:
где 
- максимальная скорость поворота лопастей винта [градусы в секунду] (полагаем, что минимальная скорость поворота равна 
); 
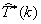- оценка значения крутящего момента двигателя в момент времени tk [отн. ед.]; Tmin, Tmax - минимальное и максимальное допустимые значения крутящего момента двигателя соответственно [отн. ед.]; TOL - погрешность [отн. ед.] (регулятор начинает изменять скорость поворота лопастей только когда значение крутящего момента близко к максимально или минимально допустимым значениям на величину TOL); 
- ошибка рассогласования [градусы]; smooth значение позволяет «гладко» изменять скорость поворота лопастей винта, когда текущий угол поворота находится близко от заданного (с помощью уменьшения управляющего воздействия на величину отклонения текущего значения угла от заданного).
Система судна подвергнута внутренним возмущениям, которые могут быть описаны изменением компонент матриц параметров системы.
С физической точки рассмотрения возмущений предположим, что в определённые моменты времени (табл.1) движущая сила F и скорость судна V увеличиваются на 10%.
Таблица 1. Моменты времени влияния возмущений
|
Время, cек. |
0.12 |
0.19 |
0.23 |
Таким образом,
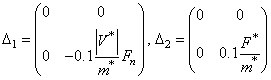(4)
А матрицы параметров:
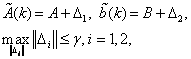(5)
Радиус устойчивости системы 
, размах неопределённостей 
Таким образом, при наличии данных неопределённостей система остаётся устойчивой.
Время влияния возмущений на систему длится 0.005 секунды.
Значение отклонения состояния системы в k-й момент времени от номинального состояния без возмущений определяется, как значение квадратичной функции Гамильтона и может быть найдено в виде [1]:
(6)
где 
- вектор состояния системы, найденный с помощью прогноза на один шаг дискретной модели:
(7)
где 
- матрицы параметров, вектора пространства состояний и управления в предыдущий ((k - 1)-й) момент времени соответственно.
Для определения интенсивности наложенных возмущений вычисляется сумма Фробениусовых норм разниц матриц параметров:
(8)
матрицы системы, найденные по компонентам вектора номинального состояния .
. (9)
Чем меньше значение параметра S(k) тем меньше уровень чувствительности системы к влиянию внутренних возмущений; если 
, то система неустойчива. Таким образом, можно использовать значение S(k) в качестве коэффициента усиления для устойчивого регулятора.
Следовательно, робастное управление может быть сформировано как:
(10)
где каждый множитель произведения описан выше.
Значение робастного управления добавляется к адаптивному значению управления, и итоговое значение определяется выражением:
(11)
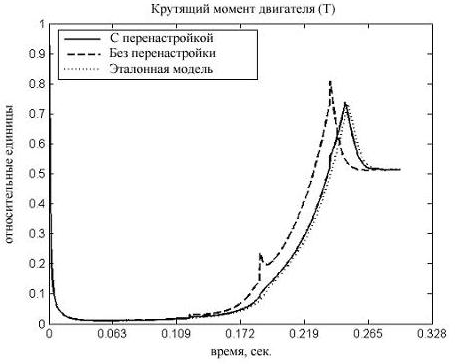
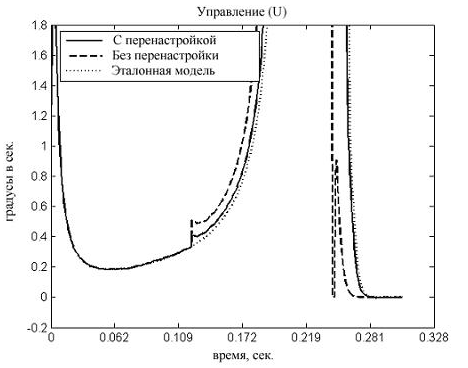
Рис. 3 - Момент двигателя (слева) и скорость поворота лопастей винта судна (справа)
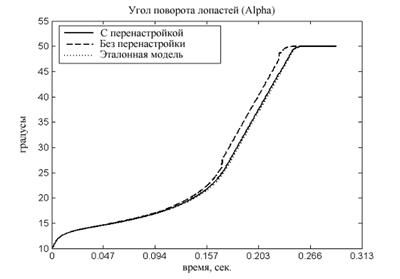
Рис. 4 - Результаты моделирования (угол поворота лопастей винта)
Определены оценки среднеквадратичного отклонения переходных процессов по углу поворота лопастей от эталонной траектории: 2.5353 для алгоритма управления без робастного регулятора и 0.4174 - с ним. Исходя из полученных результатов, можно заключить, что робастная перенастройка параметров адаптивного регулятора обеспечивает компенсацию влияния возмущений, что свидетельствует о её эффективности.
СПИСОК ЛИТЕРАТУРЫ:
- Краснов И.Ю. Adaptive algorithm of robust control for nonlinear non-stationary systems. Фундаментальные исследования, 2006. - №2. - С. 38-41.
Библиографическая ссылка
Краснов И.Ю. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РОБАСТНОГО УПРАВЛЕНИЯ УГЛОМ ПОВОРОТА ЛОПАСТЕЙ ГРЕБНОГО ВИНТА ВОДНОГО СУДНА // Современные наукоемкие технологии. – 2007. – № 1. – С. 39-43;URL: https://top-technologies.ru/ru/article/view?id=23996 (дата обращения: 23.11.2024).