Моделирование перемещения червей и гусениц в живой природе многозвенными системами со звеньями переменной длины и шарнирами является актуальным и востребованным вследствие широких возможностей для создания роботов, реализующих аналогичный принцип передвижения и способных перемещаться в ограниченном пространстве. Однако в настоящее время большинство исследований плоских робототехнических систем базируется на модели абсолютно твердых звеньев [1–3]. Вопросы управления плоскими механизмами рассматриваются в работах [3, 4]. Общие вопросы управления и стабилизации движения механических систем исследуются в работах [5–6]. Вопросы трения в зоне контакта с опорной поверхностью рассматриваются в работах [7–9]. Разработанные механизмы перемещаются за счет поперечного волнообразного движения тела. Роботов, перемещающихся за счет изменения длины звеньев тела, как у червя или гусеницы, продольного волнообразного переноса тела на данный момент, не выявлено. Таким образом, предложенная модель плоского робота опережает имеющиеся разработки и будет являться теоретическим фундаментом для дальнейшей практической реализации нового принципа перемещения ползающих роботов – волнообразного переноса корпуса робота за счет одновременного изменения длины звеньев и углов между звеньями.
Целью статьи является разработка нового способа перемещения плоских механизмов. Задача заключается в линеаризации системы дифференциальных уравнений движения плоского механизма и получении ее аналитического решения. Для этого необходимо составить системы дифференциальных уравнений движения, описывающих поведение рассматриваемых в статье механизмов. Следующий этап – создание нового алгоритма для синтеза целенаправленного движения плоского механизма со звеньями переменной длины. Создание нового алгоритма обусловлено новым способом перемещения на основе изменения длин звеньев и, соответственно, отсутствием переносимости результатов, полученных для моделей роботов с абсолютно твердыми звеньями. Новизна способа заключается в комбинации двух волнообразных движений звеньев робота в виде продольных и поперечных волн. В отличие от моделей с абсолютно твердыми звеньями, которые управлялись только одним моментом, создаваемым двигателем в шарнире, соединяющем звенья, для модели со звеньями переменной длины необходимы три управляющих воздействия. В добавление к моменту в шарнире необходимы еще две продольные силы, действующие вдоль звена и обеспечивающие изменение длин звеньев механизма. При этом необходимо наличие анизотропной силы трения, возникающей в зоне контакта площадок механизма, в которых сосредоточены точечные массы, с опорной поверхностью.
Модель плоского механизма с абсолютно твердыми звеньями
Рассмотрим движение плоского механизма с двумя звеньями на опорной поверхности ХОY, которая является плоскостью движения рассматриваемой системы. Модель имеет три сосредоточенные массы в точках А, В, С, которые обозначим следующим образом: в точке А расположена масса m1, в шарнире В – m0, в точке С – m2 (рис. 1).
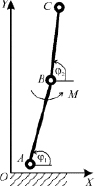
Рис. 1. Плоский механизм с тремя сосредоточенными массами и невесомыми звеньями под действием внутренних усилий и сил трения на плоскости
За обобщенные координаты, однозначно характеризующие положение механизма, выберем координаты точки В, которые обозначим х, у и углы j1, j2, которые составляют с осью ОХ звенья АВ = l1 и ВС = l2 соответственно. Все обобщенные координаты являются функциями времени.
Кинетическая энергия механизма складывается из кинетической энергии звеньев путем суммирования кинетических энергий каждой сосредоточенной на звене массы:
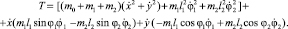 (1)
(1)
Для выбранной модели дифференциальные уравнения движения, записанные в форме уравнений Лагранжа второго рода, имеют вид
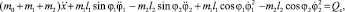 (2)
(2)
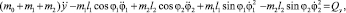 (3)
(3)
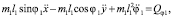 (4)
(4)
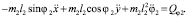 (5)
(5)
Здесь Qx, Qy, Qφ1, Qφ2 – обобщенные силы, обусловленные силами сухого трения и управляющим моментом в шарнире.
Модель плоского механизма со звеньями переменной длины с точечными площадками контакта
В этом случае звенья будем считать переменной длины, являющимися функциями времени: AB = l1(t), BC = l2(t).
Кинетическая энергия механизма складывается из кинетической энергии звеньев путем суммирования кинетических энергий каждой сосредоточенной на звене массы.
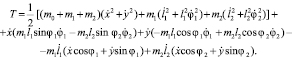 (6)
(6)
Для данной модели дифференциальные уравнения движения имеют вид
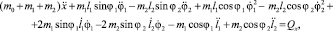 (7)
(7)
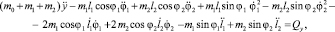 (8)
(8)
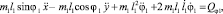 (9)
(9)
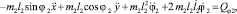 (10)
(10)
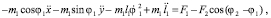 (11)
(11)
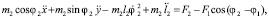 (12)
(12)
где Qx, Qy, Qφ1, Qφ2, F1, F2 – обобщенные силы, обусловленные силами сухого трения, управляющим моментом в шарнире, управляющими продольными силами, обеспечивающими изменение длины звена.
Рассмотрим разделенный на части механизм (рис. 2, слева). Покажем слева силы, действующие отдельно на звенья.
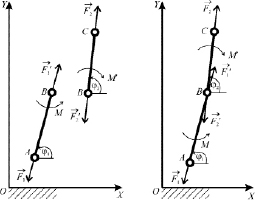
Рис. 2. Силы, обеспечивающие изменение длины звена
В соответствии с третьим законом Ньютона для звена АВ при его удлинении, т.е. движении точки А от точки В, на точку А действует сила 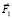 , а на точку В сила
, а на точку В сила 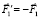 . При удлинении звена ВС, т.е. при движении точки С от точки В, на точку С действует сила
. При удлинении звена ВС, т.е. при движении точки С от точки В, на точку С действует сила 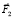 , а на точку В сила
, а на точку В сила 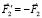 .
.
Рассмотрим соединенную модель механизма, представленную на правой части рис. 2. Звено АВ действует на звено ВС в шарнире В проекцией силы 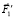 на направление звена ВС, т.е.
на направление звена ВС, т.е. 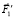 cos(j2 – j1). Соответственно, звено ВС действует на звено АВ с силой
cos(j2 – j1). Соответственно, звено ВС действует на звено АВ с силой 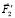 cos(j2 – j1).
cos(j2 – j1).
Линеаризация систем дифференциальных уравнений движения и их аналитическое решение
Проведем линеаризацию систем дифференциальных уравнений движения рассмотренных механизмов с целью получения аналитического решения и оценки адекватности поведения механизмов на малом промежутке времени. Рассмотрим идеальные условия, при которых на механизм не действуют внешние силы. Пусть в таких условиях находится механизм, показанный на рис. 1, с точечными площадками контакта и двумя звеньями постоянной или переменной длины. При таких условиях правая сторона системы дифференциальных уравнений движения будет равна нулю. Линеаризованная система для модели с абсолютно твердыми звеньями принимает вид
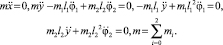 (13)
(13)
Аналитическое решение системы (13) имеет вид:
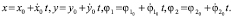 (14)
(14)
Линеаризованная система для модели со звеньями переменной длины имеет вид
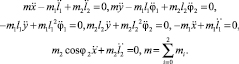 (15)
(15)
Аналитическое решение системы (15) имеет вид:
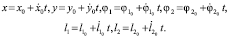 (16)
(16)
Таким образом, аналитическим решением системы линеаризованных дифференциальных уравнений движения являются уравнения равномерного движения с параметрами, зависящими от начального положения механизма. Если механизм в начальный момент времени находился в состоянии покоя, то он и будет сохранять это состояние неограниченно долго. Итак, показана адекватность системы дифференциальных уравнений движения.
Следующий этап – учет сил в правой части дифференциальных уравнений движения.
Целенаправленное движение механизма, обусловленное изменением длины его корпуса
Поступательное движение механизма реализуется за счет изменения длины звена и анизотропного покрытия нижней части робота, непосредственно контактирующей с поверхностью (рис. 3).
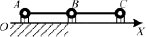
Рис. 3. Схематическая модель зон контакта, обеспечивающих анизотропное трение
Аналогия для подобной модели анизотропного трения может быть проведена с автомобильными шинами с направленным рисунком протектора, когда при движении автомобиля вперед сила трения больше, чем при движении назад. В данном случае, при движении в направлении оси х коэффициент трения меньше, чем при движении в обратном направлении. Таким образом, если проекция внутренней управляющей силы 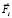 (i = 1,2), действующая на соответствующую сосредоточенную массу положительна, то сила трения меньше, чем в случае, когда проекция силы отрицательна. То есть коэффициенты трения k0, k1, k2 являются переменными, зависящими от знака проекции внутренней управляющей силы
(i = 1,2), действующая на соответствующую сосредоточенную массу положительна, то сила трения меньше, чем в случае, когда проекция силы отрицательна. То есть коэффициенты трения k0, k1, k2 являются переменными, зависящими от знака проекции внутренней управляющей силы 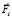 (i = 1,2).
(i = 1,2).
Перемещение из состояния покоя происходит в три этапа.
На первом этапе перемещается вперед точечная масса С за счет удлинения звена ВС под действием внутренней управляющей силы 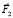 и того, что сила трения в направлении оси х меньше, чем в обратном. За счет этого достигается неподвижность точечных масс А и В.
и того, что сила трения в направлении оси х меньше, чем в обратном. За счет этого достигается неподвижность точечных масс А и В.
На втором этапе точечная масса С, сместившаяся вперед, подтягивает точечную массу В за счет внутренних управляющих сил – 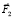 и/или ее подталкивает внутренняя управляющая сила
и/или ее подталкивает внутренняя управляющая сила 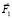 . При этом точечные массы А и С остаются неподвижными.
. При этом точечные массы А и С остаются неподвижными.
На третьем этапе сместившиеся вперед точечные массы В и С подтягивают точечную массу А за счет внутренней управляющей силы – 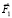 .
.
Так достигается прямолинейное движение механизма только за счет изменения длины его звеньев. При таком алгоритме перемещения возможно реализовать прямолинейное движение механизма и при обычном трении только за счет небольших значений продольных сил, чтобы была обеспечена неподвижность двух точечных масс из трех. Однако этот вопрос требует дополнительного исследования.
Следует отметить, что это не единственный возможный алгоритм прямолинейного перемещения механизма. Например, при достаточно большой анизотропии трения первый этап может выглядеть следующим образом. Перемещаются вперед точечные массы В и С, за счет удлинения звена АВ под действием внутренней управляющей силы 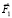 и/или еще дополнительное перемещение может получать точка С за счет внутренней управляющей силы
и/или еще дополнительное перемещение может получать точка С за счет внутренней управляющей силы 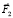 . При этом силой трения должна обеспечиваться неподвижность точечной массы А. Или второй этап может выглядеть так. Сместившая вперед точечная масса С подтягивает остальную конструкцию, состоящую из точечных масс А и В за счет действия продольных сил –
. При этом силой трения должна обеспечиваться неподвижность точечной массы А. Или второй этап может выглядеть так. Сместившая вперед точечная масса С подтягивает остальную конструкцию, состоящую из точечных масс А и В за счет действия продольных сил – 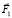 и/или –
и/или – 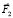 . Таким образом, будет достаточно двух этапов для организации целенаправленного движения.
. Таким образом, будет достаточно двух этапов для организации целенаправленного движения.
Если будет возможность регулировать направление анизотропного сцепления с поверхностью, робот сможет не разворачиваясь двигаться в обратном направлении.
Повороты робота реализуются за счет момента в шарнире В. Повтором и комбинацией поступательных и вращательных движений робот может реализовывать целенаправленное движение и перемещаться по плоскости в любую заданную точку.
Заключение
В результате проведенного исследования рассмотрены две модели механизмов: с точечными массами и со звеньями переменной длины. Составлены системы дифференциальных уравнений движения, проведена линеаризация и получены их аналитические решения. Предложен и описан новый алгоритм целенаправленного перемещения плоского механизма со звеньями переменной длины.



