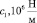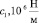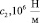К вопросам свободных колебаний механических конструкций разнообразных назначений и технической их диагностике привлечено внимание многих исследователей, в том числе в работах [1–3]. Представленная здесь работа по колебаниям ротора с гасителем продолжает подобные исследования и относится к области акустической диагностики механических систем [4, 5].
Прямая задача по свободным колебаниям ротора с гироскопическим виброгасителем рассмотрена в работах [6, 7]. В отличие от них, в данной работе по решению прямой задачи проведены исследования зависимостей частот колебаний от физических параметров ротора. Исследована также обратная спектральная задача на примере определения жесткостей опор ротора с виброгасителем. Доказана единственность решения обратной задачи и представлен алгоритм решения по известным значениям трех частот колебаний ротора.
Прямая задача определения частот свободных колебаний ротора с гасителем
Приведем некоторые теоретические сведения по прямой задаче. Ротор с виброгасителем [6] (рисунок) состоит из консольного участка оправки 1 и маховика 2. Имеются системы координат: x0y0z0 – неподвижна, x1y1z1 – движется поступательно вместе с центром масс, xyz – вращается вместе с ротором вокруг точки C относительно системы x1y1z1. В данной схеме: C – центр масс; A0B0 = L – расстояние между опорами; α – угол между осью вала z и проекцией на плоскость y1z1; β – угол между осью вала z и проекцией на плоскость x1z1; с1 и с2 – постоянные коэффициенты жесткостей опор A0 и B0 ротора по всем приведенным направлениям.
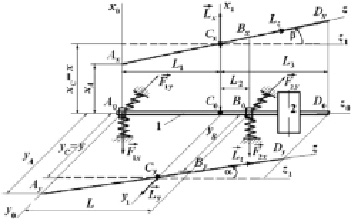
Схема оправки с виброгасителем: 1 – вал оправки (ротор), 2 – маховик
Действие виброгасителя учитывает гироскопический эффект, возникающий при перемещении оси вращения z0 вала оправки 1 за счет ее колебаний в направлении z.
За обобщенные координаты приняты координаты точки C 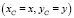 и угловые координаты α и β. Перемещения оси вращающегося ротора в положения, соответствующим проекциям AxBx и AyBy, приводят к зависимостям [6]:
и угловые координаты α и β. Перемещения оси вращающегося ротора в положения, соответствующим проекциям AxBx и AyBy, приводят к зависимостям [6]:
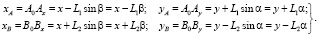 (1)
(1)
В равенствах (1) ввиду малости углов α и β принимаем 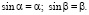
Для рассматриваемой механической системы с четырьмя степенями свободы уравнения Лагранжа имеют вид
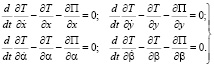 (2)
(2)
Здесь T и П – функции кинетической и потенциальной энергии ротора [6]:
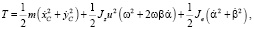
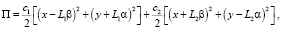
где m – масса ротора, Je = Jx = Jy, Jz – центральные моменты инерции, 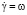 – угловая скорость вращения ротора вокруг оси z.
– угловая скорость вращения ротора вокруг оси z.
Тогда уравнения (2) с учетом выражений функций T и П примут вид
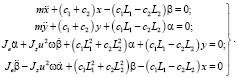 (3)
(3)
Полученные равенства (3) полностью описывают свободные колебания ротора с виброгасителем.
Учитывая, что ротор совершает свободные колебания, примем решения системы (3) в виде
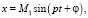
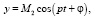
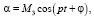
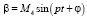 ,
,
где p – частота, 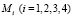 – амплитуды колебаний. Подставляя функции x, y, α, β и их производные в (3) получим [7]:
– амплитуды колебаний. Подставляя функции x, y, α, β и их производные в (3) получим [7]:
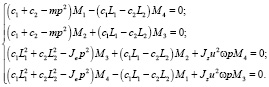 (4)
(4)
Учитывая условие существования ненулевого решения [8] системы (4) относительно амплитуд 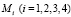 , получим следующее частотное уравнение:
, получим следующее частотное уравнение:
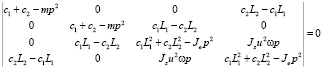 . (5)
. (5)
Раскрыв определитель (5) при известных физических параметрах ротора, находим значения частот его свободных колебаний.
Исследуем теперь влияние характеристик ротора на собственные частоты его колебаний. При этом решая прямую задачу, получим, что увеличение массовых параметров ротора ведет к уменьшению частот его колебаний. В табл. 1, например, представлена зависимость собственных частот колебаний от массы ротора при физических параметрах
Je = 1,5 кг•м2, u = 5,
ω = 10000c-1, 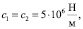
Jz = 0,031•кг м2, L1 = 0,48 м, L2 = 0,02 м. (6)
Подобные уменьшения всех частот колебаний наблюдаются и при увеличении значений центральных моментов Je, Jz инерции ротора.
Таблица 1
Зависимость частот pi от массы ротора при его параметрах (6)
|
m, кг |
р1, с–1 |
р2, с–1 |
р3, с–1 |
р4, с–1 |
|
7,5 |
79,11 |
1115,54 |
1184,47 |
5314,7 |
|
8 |
79,09 |
1079,31 |
1148,05 |
5278,13 |
|
8,5 |
79,07 |
1046,33 |
1114,91 |
5235,42 |
|
9 |
79,05 |
1016,14 |
1084,58 |
5199,74 |
Исследования показывают также, что увеличение жесткостных параметров ротора с гасителем ведет к увеличению частот его колебаний. Например, в табл. 2 приведены значения частот, соответствующие коэффициенту c1 жесткости левой опоры (при фиксированном коэффициенте c2 жесткости правой опоры) при параметрах (6) системы и массе ротора m = 7,5 кг. Подобная зависимость частот колебаний от меняющихся коэффициентов жесткостей обоих опор ротора представлена в табл. 3.
Таблица 2
Зависимость частот рi от жесткости c1 опоры ротора при параметрах (6)
|
|
р1, с–1 |
р2, с–1 |
р3, с–1 |
р4, с–1 |
|
5 |
79,11 |
1115,54 |
1184,47 |
5314,70 |
|
6 |
86,08 |
1159,00 |
1250,37 |
5344,11 |
|
7 |
91,85 |
1199,20 |
1314,14 |
5373,46 |
|
8 |
96,69 |
1236,58 |
1375,97 |
5402,74 |
Таблица 3
Зависимость частот рi от c1 жесткостей опор ротора при параметрах (6)
|
|
|
р1, с–1 |
р2, с–1 |
р3, с–1 |
р4, с–1 |
|
5 |
5 |
79,11 |
1115,54 |
1184,47 |
5314,70 |
|
6 |
6 |
94,58 |
1217,31 |
1300,18 |
5344,12 |
|
7 |
7 |
109,94 |
1310,08 |
1406,93 |
5373,46 |
|
8 |
8 |
125,19 |
1395,70 |
1506,58 |
5402,74 |
Отметим также, что подобные зависимости наблюдаются и при физических параметрах ротора, отличных от (6). Проведенные исследования важны для решения проблемы сохранения безопасных частот колебаний ротора, связанных с изменениями его физических параметров.
Обратная задача и метод ее решения
К задаче определения частот колебаний ротора с виброгасителем рассмотрим обратную задачу диагностирования его характеристик. Решение такой задачи приведем на примере определения по известным частотам колебаний коэффициентов c1 и c2 жесткостей опор ротора.
Для решения поставленной задачи преобразуем уравнение (7) к виду
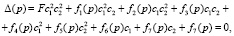 (7)
(7)
в котором 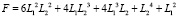 и функции
и функции 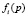 (
(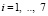 ) выражаются через физические параметры ротора:
) выражаются через физические параметры ротора:
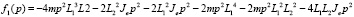 ,
,
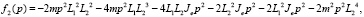
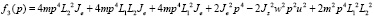 ,
,
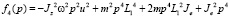 ,
,
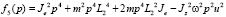 , (8)
, (8)
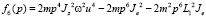 ,
,
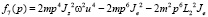 ,
,
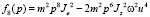 .
.
Рассмотрим сначала вопрос о существовании решения задачи. Задачу с частотным уравнением (7) обозначим через L, а задачу с такими же физическими параметрами (функциями (8)) и подобным частотным уравнением
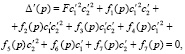
но с другими коэффициентами 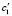 и
и 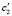 жесткостей опор ротора обозначим через L'. Тогда можно показать справедливость следующей теоремы о единственности решения поставленной обратной задачи.
жесткостей опор ротора обозначим через L'. Тогда можно показать справедливость следующей теоремы о единственности решения поставленной обратной задачи.
Теорема. Если частотные уравнения Δ(p) и Δ'(p) задач L и L' имеют вещественные корни (собственные частоты), совпадающие с учетом их кратностей, то выполняются равенства: 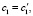
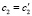 .
.
Доказательство. Очевидно, что вещественные корни уравнения (7) и являются собственными частотами спектральной задачи L. Причем частотное уравнение (7) является целой функцией от параметра p. Численными методами с помощью команд пакета Maple несложно показать, что функции (8) являются линейно независимыми.
Так как Δ(p) и Δ'(p) – целые функции, отличные от нуля, то по теореме Адамара [8] они восстанавливаются по параметру p с точностью до постоянного множителя K: 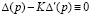 . Из последнего равенства и линейной независимости функций (8) получаем, что K = 1, откуда:
. Из последнего равенства и линейной независимости функций (8) получаем, что K = 1, откуда: 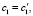
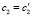 . Теорема доказана.
. Теорема доказана.
Из теоремы следует, что коэффициенты c1 и c2 жесткостей опор ротора можно определить по известным собственным частотам колебаний единственным образом.
Построим теперь метод нахождения жесткостей c1, c2 опор ротора. Пусть даны три собственные частоты p1, p2 и p3. Подставив их в уравнение (9), имеем следующие системы нелинейных относительно искомых параметров c1, c2 уравнений
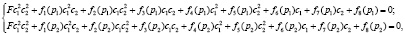 (11)
(11)
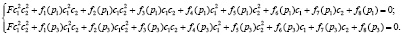 (12)
(12)
Решив (11) и (12), получим несколько наборов вещественных решений каждой из систем. Общее единственное решение этих систем и будет искомым набором значений (c1, c2).
Пример. Определить коэффициенты жесткостей опор ротора с гасителем при известных значениях трех частот колебаний 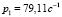 ,
, 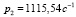 ,
, 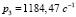 и следующих физических параметрах механической системы: Je = 1,5 кг•м2, m = 7,5 кг, ω = 10000c-1, u = 5, Jz = 0,031•кг м2, L1 = 0,48 м, L2 = 0,02 м.
и следующих физических параметрах механической системы: Je = 1,5 кг•м2, m = 7,5 кг, ω = 10000c-1, u = 5, Jz = 0,031•кг м2, L1 = 0,48 м, L2 = 0,02 м.
Решение. Подставляя заданные физические параметры ротора в (8) при частотах p1 и p2, получим, что система (11) имеет вещественные решения (найденные с помощью программы в командах математического пакета Maple):
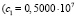 ;
; 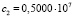 ),
),
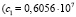 ;
; 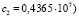 .
.
Система (12) при частотах p1, p3 и функциях (8) имеет при этом решения, имеющие физический смысл:
(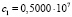 ;
; 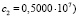 ,
,
(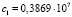 ;
; 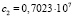 ),
),
(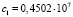 ;
; 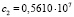 ),
),
(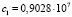 ;
; 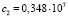 ).
).
Сравнивая полученные решения двух систем уравнений, видим, что общим для них является лишь один набор переменных (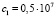 ;
; 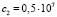 ), который и будет искомым. Значит, коэффициенты жесткостей опор равны:
), который и будет искомым. Значит, коэффициенты жесткостей опор равны: 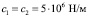 . Заметим, что по решению прямой задачи именно этим жесткостям опор соответствуют заданные значения собственных частот колебаний ротора с гасителем.
. Заметим, что по решению прямой задачи именно этим жесткостям опор соответствуют заданные значения собственных частот колебаний ротора с гасителем.
Заключение
В представленной работе по решению прямой задачи свободных колебаний ротора с гироскопическим гасителем исследовано влияние на частоты колебаний его физических параметров. Впервые поставлена и решена обратная спектральная задача – задача диагностирования характеристик ротора с гасителем по известным частотам его свободных колебаний. Доказана теорема о единственности решения поставленной задачи диагностирования. Найден метод решения задачи, который сводится к решению двух систем нелинейных уравнений при известных значениях трех частот колебаний ротора. Практическая значимость результатов состоит в возможности по найденному алгоритму определения и других характеристик (например, массовых) ротора с гасителем по его шуму. Кроме того, метод решения исследованной задачи можно применить при акустическом диагностировании характеристик и (или) условий закреплений других механических систем и их составляющих в виде роторов, валов, стержней и т.д.
Исследование выполнено при финансовой поддержке РФФИ и Правительства Республики Башкортостан в рамках научного проекта № 17-41-020230-р_а.