Задачи с параметрами уверенно вошли в материалы государственной итоговой аттестации и единого государственного экзамена по математике. Их решение вызывает немалые трудности у учащихся, которые могут быть объяснены отсутствием в ныне действующих учебниках четких методических указаний по решению задач данного класса.
Психологов всегда интересовал процесс усвоения знаний и умений учащимися. Как правильно организовать работу по усвоению знаний и умений учащимися? Ответить на этот вопрос позволила теория поэтапного формирования умственных действий П.Я. Гальперина.
Классно-урочная форма обучения, на наш взгляд, позволяет организовывать следующие этапы данной теории: ориентировка школьников в материале и способах работы с ним; осуществление пошагового контроля за усвоением каждого действия каждым школьником в ходе решения задачи; переход от пошагового контроля школьников к их самоконтролю [4].
Приведем примеры разработанных нами систем заданий по теме «Квадратные уравнения с параметрами» [2]. При их составлении мы руководствовались тем, что:
– число задач, входящих в систему, должно быть достаточным для организации каждого из этапов теории;
– сложность задач в системе должна нарастать постепенно;
– последовательность задач должна способствовать активному участию школьников в моделировании ориентировочной основы формируемого действия.
Изучение данной темы необходимо начать с рассмотрения неполных квадратных уравнений с параметрами.
Задание 1. При всех значениях параметра а решить уравнения:
1) ax2 = 0;
2) (a – 2)(x – 1)2 = 0;
3) 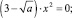
4) 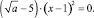
Далее переходим к решению приведенных квадратных уравнений, числовое значение дискриминанта которых представляет собой квадрат целого числа.
Задание 2. При всех значениях параметра а решить уравнение
x2 + 5ax = 14a2.
x2 + 5ax – 14a2 = 0; D = 25a2 + 56a2 = 81a2;
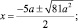
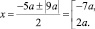
Ответ: при всех действительных значениях параметра а уравнение имеет корни x = –7a и x = 2a.
Задание 3. При всех значениях параметра а решить уравнения:
1) x2 = –6ax – 8a2;
2) x2 – 18a2 = 3ax;
3) x2 + 8ax + 7a2 = 0;
4) x2 – 15a2 = 2ax.
Следующим этапом решения квадратных уравнений с параметром является решение уравнений, дискриминант которых есть полный квадрат некоторого двучлена.
Задание 4. При всех значениях параметра а решить уравнение
x2 + (4 – 2a)x = 8a.
x2 + (4 – 2a)x – 8a = 0;
x2 + 2(2 – a)x – 8a = 0;
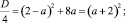
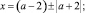
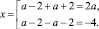
Ответ: при всех действительных значениях параметра а уравнение имеет корни x = 2a и x = –4.
Решение вышепредставленных уравнений позволяет составить ориентировочную основу действий (ООД) для решения квадратных уравнений с параметрами данного типа.
ООД решения квадратных уравнений с параметрами
• Привести уравнение к стандартному виду.
• Найти дискриминант квадратного уравнения.
• Найти контрольное значение параметра, исследуя дискриминант.
• Найти корни уравнения при контрольном значении параметра.
• Найти корни уравнения при остальных значениях параметра.
• Заполнить развертку по параметру и записать ответ.
Развертка по параметру позволяет систематизировать, обобщить и интерпретировать полученные результаты [3]. Далее учащиеся должны познакомиться с новым для них приемом решения квадратных уравнений – понижения степени. Овладевая им, учащиеся начинают понимать, что при определенных значениях параметра, квадратное уравнение приобретает статус линейного, решение которых учащимся известно [5, 6].
Задание 5. При всех значениях параметра а решить уравнение
(2a – 3)x2 + a + 1 = (3a – 2)x.
Для решения данного уравнения воспользуемся приемом понижения степени. Приравняем к нулю коэффициент при x2 и найдем значение параметра а, при котором квадратное уравнение превращается в линейное:
2a – 3 = 0; a = 1,5.
При a = 1,5 исходное уравнение принимает вид
–(3•1,5 – 2)x + 1,5 + 1 = 0,
откуда x = 1.
Найдем корни уравнения
(2a – 3)x2 – (3a – 2)x + a + 1 = 0
для всех a - 0:
D = (3a – 2)2 – 4(2a – 3)(a + 1);
D = a2 – 8a + 16; D = (a – 4)2;
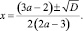
Анализируя значения дискриминанта, получаем контрольное значение параметра a = 4. Для a = 4 исходное уравнение имеет корень четной кратности x = 1.
Если a ≠ 1,5 и a≠ 4, то
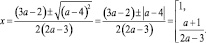
Ответ: a = 1,5; a = 4: x = 1;
a ≠ 1,5 a ≠ 4: x = 1, 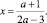
Если при решении задания 5 дискриминант представлял собой полный квадрат двучлена, то уравнение задания 6 не обладает данным преимуществом. Поэтому при его решении необходимо провести полное исследование дискриминанта (квадратного трехчлена).
Задание 6. При всех значениях параметра а решить уравнение
(a – 2)x2 – 2ax = 3 – 2a.
Преобразуем уравнение к стандартному виду
(a – 2)x2 – 2ax + 2a – 3 = 0
и применим к нему прием понижения степени.
Если a – 2 = 0, то a = 2, и уравнение принимает вид –4x + 1 = 0, откуда x = 0,25.
Если a ≠ 2, то
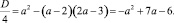
Исследуем дискриминант:
1. Если
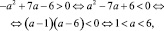
то уравнение имеет два корня. Получили два новых контрольных значения параметра а: и
Если a = 1, то уравнение принимает вид
x2 + 2x + 1 = 0,
откуда x = –1.
Если a = 6, то уравнение принимает вид
4x2 – 12x + 5 = 0,
откуда x = 1,5.
Если 1 < a < 6, то
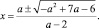
2. Если
(a – 1)(a – 6) > 0,
то уравнение не имеет корней.
Ответы: a = 1: x = –1; a = 2: x = 0,25;
a = 6: x = 1,5;
1 < a < 2 и 2 < a < 6:
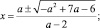
a < 1 и a > 6: решений нет.
Овладение новым приемом решения квадратных уравнений ставит вопрос о корректировке ООД решения квадратных уравнений с параметрами.
ООД решения квадратных уравнений с параметрами
• Привести уравнение к стандартному виду.
• Найти контрольные значения параметра, используя прием понижения степени уравнения.
• Найти корни уравнения при этом значении параметра.
• Найти дискриминант квадратного уравнения.
• Найти контрольное значение параметра, исследуя дискриминант.
• Найти корни уравнения при новых контрольных значениях параметра.
• Найти корни уравнения при остальных значениях параметра.
• Заполнить развертку по параметру и записать ответ.
Усвоить ориентировочную основу решения полных квадратных уравнений с параметрами можно при помощи уравнений задания 7.
Задание 7. При всех значениях параметра а решить уравнения:
1) ax2 + (a + 1)x + 1 = 0;
2) (a – 1)x2 + 1 = 2x + a;
3) (b – 2)x2 + 3b +2 = 4bx;
4) ax2 = (a + 1)x + 1 + 2a.
Далее переходим к рассмотрению дробно-рациональных уравнений с параметрами, решение которых сводится к решению квадратных уравнений. При решении уравнений данного вида необходимо с самого начала указывать значения параметра и переменной, при которых уравнение имеет смысл. Знание области допустимых значений переменной и параметра позволяет в дальнейшем исследовать корни уравнения.
Изучение дробно-рациональных уравнений начинаем с уравнений, числитель которых представляет собой квадратный трехчлен в самом «хорошем случае» – его дискриминант является полным квадратом.
Задание 8. При всех значениях параметра а решить уравнение
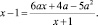
Укажем область допустимых значений переменной х: x ≠ –1.
Преобразуем уравнение к стандартному виду
x2 – 6ax + 5a2 – 4a – 1 = 0
и найдем его корни:
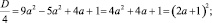
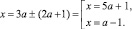
Найденные корни должны быть отличны от нуля, то есть 5a + 1 ≠–1 или a – 1 ≠ –1. Откуда a ≠ –0,4, a ≠ 0.
Найденные значения параметра а представляют собой его контрольные значения. При них исходное уравнение имеет один корень x = 1 или x = –1,4.
Ответ:
a ≠ –0,4: x = –1,4;
a ≠ 0: x = 1;
a ≠ –0,4, a ≠ 0: x = 5a + 1; x = a – 1.
Задание 9. При всех значениях параметра а решить уравнение
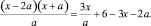
Решение данного уравнения требует ограничений на параметр: a ≠ 0. При этом условии исходное уравнение равносильно уравнению
x2 – (2a – 3)x – 6a = 0.
Решая его, находим, что x = 3 или x = –2a. Записываем ответ.
Ответ:
a = 0: решений нет;
a ≠ 0: x = 3; x = –2a.
Далее знакомим учащихся с решением дробно-рациональных уравнений, решение которых сводится к квадратному уравнению с дискриминантом, не являющимся полным квадратом. Учащиеся понимают, что в этом случае корень из дискриминанта не извлекается, и они сталкиваются с необходимостью решать иррациональные уравнения, что довольно трудоемко, особенно для детей, которые по возрастным показателям еще не владеют техникой их решения. В этом случае на помощь может прийти прием, ведущий к цели более коротким и технически простым путем.
Задание 10. При всех значениях параметра а решить уравнение
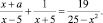
Запишем ограничения на значения переменной x: x ≠ ±5. После необходимых преобразований, перейдем к системе, равносильной исходному уравнению:
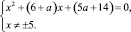
Дискриминант квадратного трехчлена, стоящего в левой части уравнения, равен
D = 36 + 12a + a2 – 4(5a + 14) = a2 – 8a – 20.
Так что для того, чтобы уравнение имело корни, необходимо, чтобы a2 – 8a – 20 ≠ 0. Последнее неравенство выполняется для a ≠ –2 или a ≠ 10.
При остальных значениях параметра а квадратное уравнение решений не имеет и, тем более, не имеет решений исходное уравнение.
Итак, при a ≠ –2 или a ≠ 10 квадратное уравнение имеет два корня
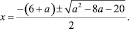
Исключим посторонние корни. Для этого найдем значения параметра а, при которых х будет равняться 5 или –5:
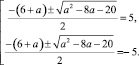
Выполнение данных условий требует решения четырех иррациональных уравнений.
Выйти из затруднительного положения позволяет следующее рассуждение: каждое значение параметра задает свое, соответствующее только этому значению параметру, уравнение. Естественно, что каждое уравнение, в свою очередь, предполагает свой «набор» корней. Значит, справедливо и обратное: определенному значению переменной х соответствует «свое» значение параметра а.
Поэтому вычислим значения квадратного трехчлена в «запрещенных» точках:
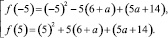
Тогда
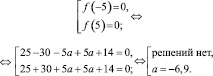
Итак, если a = –6,9, то
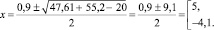
Но x = 5 не является корнем, следовательно, остается корень x = –4,1.
Для завершения решения, найдем корни уравнения в контрольных точках a = –2 и a = 10: если a = –2, то x = –2; если a = 10, то x = –8.
Ответ:
a = –6,9: x = –4,1;
a = –2: x = –2;
a = 10: x = –8;
–2 < a < 10: решений нет;
a < –6,9; –6,9 < a < –2; a > 10:
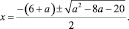
В свете рассмотренных дробно-рациональных уравнений с параметрами внесем дополнения в ориентировочную основу решения уравнений, сводимых к квадратным.
ООД решения дробно-рациональных уравнений с параметрами
• Найти области допустимых значений переменной и параметра.
• Привести уравнение к стандартному виду.
• Найти контрольное значение параметра, используя прием понижения степени уравнения.
• Найти корни уравнения при этом значении параметра.
• Найти дискриминант квадратного уравнения.
• Найти контрольные значения параметра, исследуя дискриминант.
• Найти корни уравнения при новых контрольных значениях параметра.
• Найти контрольные значения параметра по области допустимых значений переменной, используя прием подстановки «запрещенных» значений переменной в формулу корней квадратного уравнения.
• Найти корни уравнения при остальных значениях параметра.
• Заполнить развертку по параметру и записать ответ.
Составленная ориентировочная основа решения квадратных уравнений и уравнений, к ним сводимых, позволяет выделить приемы нахождения контрольных значений параметра, от знания которых зависит решение уравнения:
1. Нахождение области допустимых значений параметра.
2. Использование приема понижения степени уравнения.
3. Исследование дискриминанта.
4. Исключение посторонних корней уравнения по области допустимых значений переменной (прием подстановки «запрещенных» значений переменной в формулу корней квадратного уравнения).
Рассмотрим решение дробно-рационального уравнения с параметром, сводимого к квадратному, которое сочетает в себе использование всех выделенных приемов нахождения контрольных значений параметра.
Задание 11. При всех значениях параметра а решить уравнение
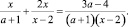
Областью допустимых значений переменной являются все x ≠ 2, параметра – все a ≠ –1.
При a = –1 уравнение не имеет смысла, а значит, не имеет решений.
Преобразуем уравнение к виду
x2 + 2ax + 4 – 3a = 0
и найдем его корни, отличные от 2. Дискриминант квадратного трехчлена, стоящего в левой части уравнения, равен
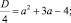
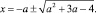
Естественно, для того чтобы уравнение имело решения, дискриминант должен быть неотрицательным:
a2 + 3a – 4 ≥ 0,
откуда 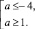
Получили новые контрольные значения параметра а: a = –4 и a = 1.
Если a = –4, то x = 4. Если a = 1, то x = –1.
Составим уравнение, позволяющее найти те значения параметра а, при которых переменная х принимает значение 2:
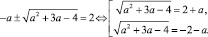
Видим, что для нахождения контрольных значений параметра а, при которых корни уравнения принимают статус «запрещенных», необходимо решить два иррациональных уравнения. Чтобы избежать этого, воспользуемся рассмотренным выше приемом и найдем новые контрольные значения параметра а, подставив в уравнение
x2 + 2ax + 4 – 3a = 0,
«запрещенные» значения переменной x:
22 + 2a•2 + 4 – 3a = 0,
откуда a = –8. Систематизируем полученные решения и запишем ответ.
Ответ:
a = –8: x = 14;
a = –4: x = 4;
a = 1: x = –1;
–4 < a < 1, a ≠ –1: решений нет;
a ≠ –8, –4 < a, a > 1: 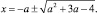
Предлагаемая методика построения ООД позволяет обучить школьников решению целого класса задач с параметрами, а совместное выделение приема нахождения контрольных значений готовит учащихся к осуществлению исследовательской деятельности, освоению профессионально значимых умений [1].



