Физика является основой формирования научных знаний о природе, на ее основе формируется мировоззрение выпускника технического вуза. Усвоение технических наук, овладение навыками инженерного искусства во многом зависит от системности и фундаментальности физико-математического образования в вузе.
Проблема формирования научного мировоззрения в процессе обучения физике отражена в работах В.Ф. Ефименко, Л.Я. Зориной, Р.Х. Казакова [2], В.Н. Мощанского, В.В. Мултановского, Н.С. Пурышевой, А.А. Синявиной, А.В. Усовой, Л.С. Хижняковой [5] и др. Ими доказано, что систематизация материала курса физики на основе фундаментальных физических теорий и идеи научной картины мира, реализация единства системы знаний и методов научного познания служат основой формирования системных научных знаний, развития научного мышления обучающихся.
В физических теориях отражаются результаты научного стиля мышления, воплощаются в свернутом виде элементы цикла познания. Каждая из физических теорий исследует свой фрагмент природы, содержательная структура всех физических теорий одинакова.
Cодержательная структура физической теории как концептуальной системы состоит из диалектически взаимосвязанных элементов: эмпирического основания теории; концептуального теоретического ядра теории; дедуктивного теоретического следствия. Физическая теория образует целостную систему знаний о фрагменте природы. Ее элементы гносеологически взаимосвязаны и упорядочены [3, 4].
Каждый элемент физической теории имеет различный логический генезис. Так, эмпирическое основание физической теории формируется в ходе эмпирически-индуктивных обобщений результатов экспериментов и наблюдений. Теоретическое ядро образуется как концептуальное содержательное обобщение эмпирических закономерностей с применением диалектической логики. Дедуктивные следствия физической теории образуются с применением дедуктивного метода и представляют теоретические обобщения второго уровня.
Дедуктивный вывод теоретических следствий в физике отличается от аксиоматически-дедуктивного метода в математике. Теоремы математики как логические следствия аксиоматического основания выводятся дедуктивно без привлечения дополнительных аксиом. Частные физические законы выводятся с привлечением дополнительных утверждений и моделей.
Применяя основные законы физической теории к конкретным физическим системам, получаем теоретические дедуктивные следствия, описывающие динамику этой системы. Важнейшим признаком научного знания является его принципиальная проверяемость. Следует подчеркнуть, основные законы физической теории не поддаются непосредственной эмпирической проверке – проверке практикой. Экспериментальной проверке техническими средствами подвергаются дедуктивные следствия теоретического ядра, что подтверждает (или опровергает) истинность ядра физической теории.
Примерами дедуктивных следствий теоретического ядра классической механики являются: «Элементы динамики вращательного движения твердого тела. Элементы статики. Элементы гидростатики и гидродинамики. Элементы теории механических колебаний и волн».
Они служат иллюстрацией применения основных законов к конкретным механическим системам. Для них вводятся более сложные модели: упругое тело, пластическое тело, несжимаемая жидкость, математический маятник и др. Через теоретические следствия, дедуктивно выведенные из фундаментальных законов, реализуются объяснительная и предсказательная функции физической теории. Предсказательная функция выражается в том, что теория своими средствами и в границах применимости предсказывает изменение состояния физической системы по известному состоянию в начальный момент времени. Научный эксперимент не выявляет внутренние причинно-следственные связи в физической системе, определяющие явление. В эксперименте наблюдается внешнее проявление этих связей. Теория в границах применимости объясняет закономерности протекания, причинно-следственные связи в конкретной системе физической теории.
Элементы темы «Динамика вращательного движения твердого тела» представляет собой конкретное следствие фундаментального ядра классической механики. Здесь вводится более сложный модельный объект реального тела – абсолютно твердое тело, которое учитывает особенности свойств объектов описываемых систем (в сравнении с материальной точкой). Абсолютно твердое тело как модель реального твердого тела представляет собой непрерывную совокупность (континуум) материальных точек. В эксперименте реальное тело можно принять за абсолютно твердое, если деформация тела столь незначительна, что этой деформацией можно пренебречь.
Вращательное движение твердого тела вокруг неподвижной оси, как и поступательное движение, является основным видом движения твердого тела. Остальные разновидности движения твердого тела сводятся к одному из основных движений или к их совокупности.
Для количественного описания вращательного движения твердого тела используются кинематические характеристики этого движения: угловая скорость ω и угловое ускорение ε. Между угловым ускорением и динамическим взаимодействием на твердое тело, называемым моментом внешних сил, существует количественная связь – основное уравнение динамики вращательного движения твердого тела:  . Оно представляет трансформацию основного уравнения динамики:
. Оно представляет трансформацию основного уравнения динамики: 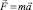 для конкретной механической системы.
для конкретной механической системы.
Тема «Элементы статики» рассматривается как раздел механики, в котором изучаются условия равновесия тел. Данную тему можно рассматривать как дедуктивное следствие теоретического ядра – раздел динамика.
Используя материал тем «Элементы гидростатики», есть возможность рассмотреть взаимосвязь физики с техникой. Так, например, действие многих гидравлических устройств – прессов, тормозных систем автомобиля, гидроприводов и гидроусилителей и т.п. – основано на законе Паскаля.
«Элементы гидродинамики несжимаемой жидкости» иллюстрируют применение фундаментальных законов классической механики для описания конкретной механической системы и подтверждают их истинность в границах своей применимости.
В окружающем нас мире и технике часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными.
Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными. Простейшим видом колебательного процесса являются простые гармонические колебания, в которых динамическая переменная s(t) описывается уравнением с использованием функций синуса (косинуса) s(t) = Acos [α(t)]. При этом колебательная система, как материальный объект, называется гармоническим осциллятором. Элементы теории механических колебаний также являются примером дедуктивного следствия ядра физической теории «Механика Ньютона». При описании процессов, происходящих в колебательных системах, мы иллюстрируем применение основных законов к конкретным механическим системам.
Рассмотрим на примере колеблющегося груза на пружине применение второго закона Ньютона для вывода уравнения движения. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Выбираем инерциальную систему координат, связанную с Землей, приняв за начало координат положение равновесия тела. Второй закон Ньютона 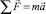 трансформируется:
трансформируется:
Fx = max,
где Fx – это упругая сила, определяемая законом Гука:
Fx = –kx.
Следовательно,
max = –kx,
откуда
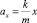 .
.
Или 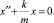 Решением этого дифференциального уравнения второго порядка является гармоническая функция: x(t) = Acos (ωt + φ). Пружинный маятник является примером гармонического осциллятора. В качестве возвращающей силы не обязательно должна быть сила упругости. Например, для математического маятника – это равнодействующая сил тяжести и упругости. Периодическая функция времени x = f(t) позволяет предсказать состояние колебательной системы со временем. Так реализуется предсказательная функция физической теории для конкретной механической системы.
Решением этого дифференциального уравнения второго порядка является гармоническая функция: x(t) = Acos (ωt + φ). Пружинный маятник является примером гармонического осциллятора. В качестве возвращающей силы не обязательно должна быть сила упругости. Например, для математического маятника – это равнодействующая сил тяжести и упругости. Периодическая функция времени x = f(t) позволяет предсказать состояние колебательной системы со временем. Так реализуется предсказательная функция физической теории для конкретной механической системы.
Для получения уравнений скорости и ускорения нужно применить закон изменения первой и второй производной. Тогда уравнение скорости
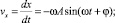
и уравнение ускорения
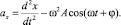
При изучении колебательных процессов важно использовать закон сохранения импульса и особенно закон сохранения энергии, которые входят с состав ядра механики Ньютона. С энергетической точки зрения колебательный процесс представляет собой периодический обмен энергией между различными элементами системы и превращение энергии одного вида, например кинетической, в другой вид энергии, например потенциальную.
Покажем, что для любого положения колеблющегося тела его полная энергия не изменяется в процессе колебаний на примере груза, совершающего свободные гармонические колебания на достаточно жесткой пружине.
Закон изменения кинетической энергии:
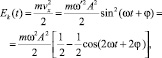
где 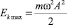 – максимальное значение кинетической энергии груза.
– максимальное значение кинетической энергии груза.
Закон потенциальной энергии:
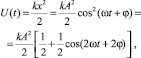
где 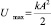 – максимальная потенциальная энергия пружины.
– максимальная потенциальная энергия пружины.
Кинетическая и потенциальная энергии изменяются с частотой 2ω, то есть в два раза большей, чем частота колебаний координаты. Сравнивая выражения для изменения потенциальной и кинетической энергий, видим, что энергии изменяются в противофазе. При свободных гармонических колебаниях собственная частота осциллятора 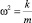 , следовательно
, следовательно
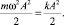
Полная механическая энергия не изменяется в процессе колебаний:
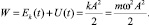
Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.
Приведем пример методики решения задачи на основе аналогии между механическими и электрическими колебаниями.
Задача. Найти период колебаний осциллятора, изображенного на рис. 1. k1 и k2 – жесткости пружин; m – масса тела.
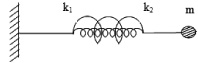
Рис. 1
Для решения такой задачи следует перейти к эквивалентной электрической системе (рис. 2). Двум пружинам механического осциллятора в электрической системе соответствуют два конденсатора, имеющие емкости C1 и C2, а массе – индуктивность L. Как должны будут соединены конденсаторы, следует дополнительно конкретизировать. В первом случае при смещении груза m на некоторое расстояние (х) каждая из пружин получит такое же удлинение (x1 и x2): х = x1 = x2. Так как смещению х соответствует заряд q, то конденсаторы следует соединить последовательно, поскольку при этом q =q1 = q2. Таким образом, получаем эквивалентную схему (рис. 2) и далее находим период электрических колебаний:
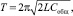
где 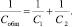
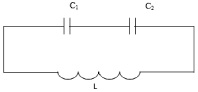
Рис. 2
Далее, используя аналогию, запишем период колебаний механического осциллятора:
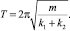
Дедуктивные следствия как теоретические обобщения второго уровня проверяются практикой. Экспериментальная проверка техническими средствами подтверждает (или опровергает) истинность ядра физической теории. Теория колебаний многократно проверена на практике и нашла широкое применение в различных технологических процессах и машинах. Примером могут служить сортировочные машины, вибрационные конвейеры, вибролитье, виброрезание и т.д. Понимание природы колебаний, умение правильно выбрать динамическую модель машины, адекватную колебательным процессам, оценить виброактивность механизмов и машины в целом, знание методов уменьшения виброактивности и методов виброзащиты машин, аппаратов, людей, а также способов полезного использования колебаний в рабочих процессах совершенно необходимы для будущего инженера. Результат решения любой физической задачи следует также рассматривать как дедуктивное следствие основных (фундаментальных) законов физической теории.
В качестве иллюстрации сказанного рассмотрим задачу одного из примеров дедуктивного следствия физической теории – «Динамика вращательного движения твердого тела».
Задача. На горизонтальную ось насажен шкив радиусом R. На шкив намотан шнур, к свободному концу которого подвесили гирю массой m. Считая массу М шкива равномерно распределенной по ободу, определить ускорение а, с которым будет опускаться гиря, силу натяжения нити Т и силу давления шкива на ось (рис. 3) [1].
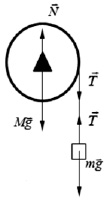
Рис. 3
Решение: Поскольку шкив только вращается, то уравнения движения шкива запишем в виде
 (1)
(1)
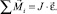 (2)
(2)
На шкив действуют силы тяжести Mg, натяжения нити Т, реакции оси N. Сила реакции оси N по третьему закону Ньютона численно равна искомой силе давления шкива на ось. Уравнение (2) можно записать в проекции на ось, направленную вертикально вниз:
Mg + T – N = 0. (3)
Шкив вращается под действием лишь момента силы Т. Следовательно, уравнение (2) дает равенство
TR = Jε. (4)
Момент инерции шкива, поскольку его масса распределена по ободу,
J = M•R2. (5)
Уравнения (3), (4) содержат три неизвестных: T, N, e. Недостающее уравнение запишем, применив второй закон Ньютона для поступательного движения гири в проекции на ту же ось:
mg – T = ma. (6)
Так как шнур сматывается без скольжения, ускорение гири равно тангенциальному ускорению точек на ободе шкива и угловое ускорение можно записать
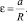 (7)
(7)
Подставив в уравнение (5) значения J, e по формулам (4) и (7) найдем из системы уравнений (3), (4), (6) неизвестные величины:
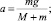
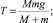
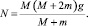
Мы видим, что решение проблемы находится с использованием уравнений динамики вращательного и поступательного движения и уравнения для ускорения и сил натяжения нити Т и давления шкива на ось получены дедуктивно с использованием эмпирического факта 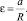
Студент в процессе практических и лабораторных работ, в ходе самостоятельной работы приобретает: навыки дедуктивного вывода следствий ядра физической теории; умения оперирования физическими понятиями; навыки и умения экспериментального исследования механических систем, навыки решения стандартных задач механики и теоретического анализа и обобщения результатов решения.
Таким образом, знание логического генезиса дедуктивных следствий физической теории служит формированию системности знаний физических теорий, развитию теоретического мышления студентов.



