Проведенный анализ трудов отечественных и зарубежных ученых в области разработки и применения методов цифровой обработки сигналов (ЦОС) позволяет заключить, что, с точки зрения основополагающих принципов построения вычислительных средств цифровой обработки сигналов, все известные технические реализации СП можно разделить на две основные группы.
К первой из них относятся вычислительные процессоры, базирующиеся на реализации ортогональных преобразований сигналов [7, с. 76, 8, с. 38-39, 9, с. 77]. Такие преобразования, как правило, определены над полем комплексных чисел и называются дискретным преобразованием Фурье (ДПФ), которое определяется выражением:
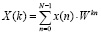. (1)
где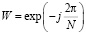 
– поворачивающий коэффициент; 
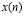– количество отсчетов, 
, 
.
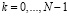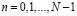Для реализации обратного преобразования сигналов используется обратное ДПФ (ОДПФ), согласно равенства
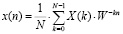, (2)
Анализ выражений (1) и (2) показывает, что значения входного сигнала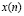 
являются подмножеством поля комплексных чисел С. В этом случае ортогональные преобразования, задаваемые выражением ДПФ и ОДПФ, так же определяются над этим полем, т. е. поле С используется для определения преобразований, применяемых при построении математической модели ЦОС. Следовательно, реализация таких моделей связана с реализацией арифметических операций поля комплексных чисел, что нельзя считать удачным. Действительно, сигнал х(п), полученный в результате АЦП, представляет собой список чисел, объем информации которого – конечная и вполне определенная величина. Осуществив преобразование этого сигнала в соответствии с выражением (1), получим сигнал X(k), числовое представление которого обладает теоретически бесконечным объемом информации, так как в результате определения модели над бесконечным полем С значения х(n) умножаются и суммируются на коэффициенты из С, часто являющиеся иррациональными числами. Известно, что иррациональное число выражается бесконечной дробью, что приводит к бесконечному объему информации цифрового представления сигнала. Практически объем информации такого представления конечен, но больше первоначального и определяется точностью представления чисел в вычислительном устройстве или, другими словами, длиной разрядной сетки. Длина разрядной сетки для представления результатов промежуточных вычислений обычно в два и более число раз превышают длину разрядной сетки, представляющие входные данные. Значит, благодаря этому непроизвольно вводится информационная избыточность и усложняются вычисления, так как они проводятся в поле комплексных чисел [1, с. 60-97, 2].
Таким образом, очевидно, что реализация прямого и обратного ДПФ предопределяет значительные погрешности при вычислении значений спектральных коэффициентов в поле комплексных чисел, обусловленных тем, что поворачивающие коэффициенты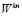 
представляют собой иррациональные числа, а это при значительных значениях N приводит к существенной аддитивной арифметической погрешности.
Вычисления спектра и восстановление по нему исходного сигнала непосредственно по выражениям (1) и (2) требует выполнения значительного числа операций умножения и сложения в поле комплексных чисел. Непосредственное вычисление ДПФ при комплексных значениях x(nT) требует для каждого значения k (N–1) умножений и (N–1) сложений комплексных чисел или 4(N–1) умножений и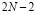 
сложений действительных чисел. Следовательно, для вычисления всех N значений коэффициентов ДПФ входного вектора x(nT) потребуется примерно N2 умножений и N2 сложений комплексных чисел. Таким образом, для больших значений N (N > 100) входного вектора прямое вычисление ДПФ согласно (1) требует весьма большего числа арифметических операций умножения и сложения, что затрудняет реализацию вычислений в реальном масштабе времени процессов и спектров [4, с. 60-97].
Лучшие показатели быстродействия получаются при использовании так называемых быстрых алгоритмов, которые существуют для ДПФ [5, с. 73-74, 14]. Исходная идея данных алгоритмов быстрого преобразования Фурье (БПФ) состоит в том, что N-точечная последовательность разбивается на две более короткие последовательности, для которых вычисляется ДПФ с последующим восстановлением исходного ДПФ. Если N=2v , v>0 и целое, то процесс уменьшения размера ДПФ может продолжаться до тех, пока не останутся только двухточечные ДПФ. При этом общее число этапов вычисления ДПФ будет равно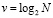 
, а число требуемых арифметических операций будет порядка 
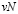, т.е. уменьшается примерно в 
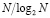раз.
При реализации БПФ возможно несколько вариантов вычислений в зависимости от способа деления последовательности отсчетов на части (прореживание по времени либо по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге, т.е. от основания БПФ. Так для прореживания по времени реализации БПФ определяется
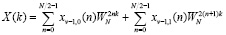, (3)
где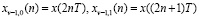 
– соответственно последовательность с четными и нечетными номерами;
.
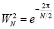Процесс вычисления коэффициентов дискретного преобразования Фурье с использованием алгоритма с прореживанием по частоте задается выражением
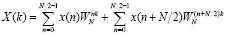, (4)
где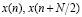 
– соответственно первая и вторая части входной последовательности отсчетов.
Необходимо отметить, что в обоих алгоритмах БПФ – и с прореживанием по времени, и с прореживанием по частоте – требуется примерно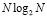 
операций комплексного умножения и оба алгоритма могут быть реализованы по способу с замещением, используя только один массив ячеек памяти. Таким образом, применение БПФ с основанием 2 позволяет выполнить более эффективное вычисление ортогональных преобразований сигналов по сравнению с прямым преобразованием (1).
В основу данных алгоритмов положен принцип разбиения исходного ДПФ на совокупность малоточечных реализаций. Различия заключаются в способах вычисления таких малоточечных алгоритмов и последующем объединение частичных результатов. При этом размер преобразований не обязательно равен степени двойки. Другими словами, становится возможность быстрой реализации ортогональных преобразований произвольной длины, что очень важно для ряда практических задач [6, с. 98-100].
В работе [11, с. 59-60] представлен обобщенный алгоритм Кули-Тьюки с произвольным основанием и поворачивающими множителями. Данный быстрый алгоритм реализации ДПФ применим в случае, если N является составным, т.е.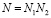 
, где N1 и N2 – положительные числа. Тогда вычисление исходного N-точечного ДПФ сводится к вычислению N1 N2 –точечных и N2 N1 –точечных ДПФ и N умножений на множители поворота 
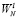. В этом случае в выражение (1) производится подстановка
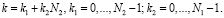(5)
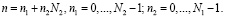(6)
Применение выражений (5) и (6) позволяет свести равенство (1) к виду
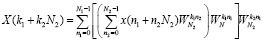. (7)
Таким образом, быстрый алгоритм вычисления ДПФ включает в себя две основные ступени: на первой ступени представленные в соответствии с (6) входные выборки подвергаются N2-точечному преобразованию Фурье на второй ступени производится вычисление N1-точечных ДПФ. Между первой и второй ступенями осуществляются операции поворота путем умножения на поворачивающие множители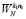 
. Полученная последовательность на выходе СП ДПФ переставляется в соответствии с (5).
Дальнейшим шагом в повышении эффективности реализации ортогональных преобразований с использованием дискретного преобразования Фурье стал алгоритм простых множителей [17, с. 22-25]. Данный алгоритм применяется когда длина входной последовательности N представима в виде произведения взаимнопростых множителей. В этом случае обеспечивается возможность сокращения числа операций умножений, за отказа от поворачивающих множителей, используемых в (7).
Для этого производится перестановка входной последовательности согласно условия
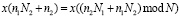, (8)
где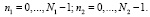 
А перестановка выходной последовательности определяется
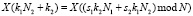, (9)
где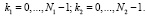 
При этом значения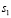 
и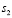 
задаются из следующих уравнений в соответствии с китайской теоремой об остатках
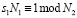, (10)
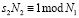. (11)
В этом случае алгоритм вычисления ДПФ представляется в виде
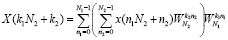. (12)
Таким образом, алгоритм простых множителей является способом представления одномерного ДПФ в виде многомерного, причем размерность зависит от числа простых сомножителей N. Алгоритм простых множителей имеет ступенчатую форму объединения малоточечных преобразований. При этом на первой ступени производится N1 N2 –точечных ДПФ, а на второй ступени – N2 N1 –точечных ДПФ. Отказ от выполнения поворота промежуточных результатов по первой координате позволил сократить время вычисления ДПФ более чем на 10 процентов по сравнению с алгоритмом (6).
Дальнейшее сокращение времени реализации ортогональных преобразований сигналов возможно достичь если ступенчатый характер объединения частичных малоточечных преобразований заменить вложенным [12, с. 76-78]. В некоторых работах представлен алгоритм Винограда используемый для быстрого вычисления ДПФ. Применение последнего позволяет сократить число операций умножений по сравнению с БПФ в 2-3 раза при незначительном увеличении числа сложений.
В основу алгоритма Винограда положена замена длинного преобразования ДПФ серией коротких путём построения гнездового алгоритма, аналогичному алгоритму вычисления, свёрток, и сведение коротких преобразований к циклическим свёрткам. При этом при построении гнездового алгоритма используется КТО.
Пусть дано ортогональное преобразование в поле комплексных чисел длины N, выполняемое согласно (1.1), причем N=N1N2 и НОД(N1,N2)=1. Тогда используя КТО, представим показатель kn поворачивающего коэффициента W в модулярном коде.
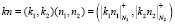, (13)
где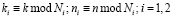 
.
Для осуществления обратного преобразования к позиционному виду используется КТО, согласно которой
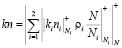. (14)
где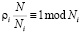 
.
Тогда ДПФ, в модулярном коде вычисляется
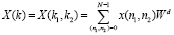, (15)
где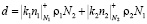 
.
Применение китайской теоремы об остатках позволяет перейти от вычисления одномерного ДПФ к многомерному согласно выражения
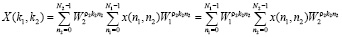. (16)
Выражение (16) соответствует определению двумерного ДПФ с ядрам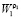и 
и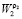 
. Таким образом, гнездовой алгоритм Винограда сводит вычисление одномерного ДПФ к двухмерному, если строки и столбцы матрицы преобразования и исходных данных представить в соответствии с КТО. При этом вычисление ДПФ проводится в 3 этапа:
1) переставляются строки и столбцы матрицы ДПФ и отсчётов последовательности xi(n) в соответствии с КТО.
2) выполняется двумерное ДПФ, соответствующее внутренней сумме выражения (16)
3) результаты внутреннего преобразования, являются вектором над которыми выполняется внешнее ДПФ, соответствующее внешней сумме (16).
Оптимальные алгоритмы для вычисления малоточечных ДПФ при N≤16 приведены в работе [13, с. 71-73]. Гнездование этих алгоритмов позволяет эффективно осуществлять вычисления ДПФ длинных последовательностей.
Если положить, что значение N=N1, N2,…Ni, где НОД (Ni,Nj)=1, то тогда вычисление ДПФ по алгоритму Винограда сводиться к вычислению малоточечных преобразований размером Ni, i =1,2, … d. При этом если для реализации преобразований размера Ni потребуется Mi комплексных умножений и Ai комплексных сложений соответственно равно
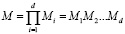, (17)
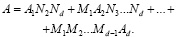(18)
Очевидно, что число сложений (18) зависит от порядка выполнения операций. Поэтому наиболее оптимальным считается такой порядок, при котором количество операций минимально.
Рассмотренные алгоритмы ускоренного вычисления ортогональных преобразований сигналов, связанные с применением быстрых алгоритмов ДПФ, являются распространенными и универсальными способами сокращения объема вычислений. Однако при их использовании вычисления выполняются с трансцендентными (тригонометрическими) функциями, что приводит к накоплению аддитивных погрешностей при увеличении размерностей задачи [15, с. 23-24, 16, с. 22-23]. Более того, для реализации БПФ требуется двухканальный вычислитель для обработки действительной и мнимых частей сигнала, что требует значительных схемных затрат, и в конечном итоге приводит к резкому снижению надежности всей вычислительной системы. Поэтому для уменьшения среднеквадратической погрешности вычислений и повышению надежности функционирования СП ЦОС целесообразно обратить внимание на группу алгоритмов цифровой обработки сигналов, в которой бы не используются операции поля комплексных чисел [18].