В Федеральном законе «Об образовании в Российской Федерации» № 273-Ф3 от 29 декабря 2012 года, «Национальной доктрине образования Российской Федерации до 2025 года», Федеральных образовательных стандартах общего образования и высшего профессионального образования сделан акцент на необходимость овладения обучающимися процессом творчества (поиск идей, рефлексия, моделирование, выдвижение гипотез и их доказательство и т.д.), культурой мышления, развития у них креативных способностей.
Креативность трактуется учёными как дивергентное мышление (Дж. Гилфорд,
Е.П. Торенс, М.А. Холодная); творческие интеллектуальные способности (Ф.Баррон); система личностных качеств, побуждающих личность к творческой самореализации и саморазвитию (В.Г. Рындак); интеллектуальная активность (Д.Б. Богоявленская); способность порождать оригинальные идеи в условиях разрешения или постановки новых проблем (А. Олах); интегральное социально значимое личностное качество (Л.С. Выготский, М. Вертгеймер, Дж. Гильфорд, В.М. Дружинин, О.К. Тихомиров) и др.
Креативное мышление личности проявляется в конструктивной деятельности в совокупности способностей и умений генерировать новые нестандартные идеи, выбирать продуктивные способы решения задач.
Средством развития креативного мышления, как показывает практика, являются познавательные задачи, решение которых предполагает интеллектуальную активность, генерирование новых идей, поиск продуктивных оригинальных решений.
Есть различные подходы к определению познавательных задач (Г.А. Балл, Л.Л. Гурова,
А.В. Брушлинский, И.Я. Лернер, А.М. Матюшкин и др.). Мы, следуя П.Г. Лабзиной, под познавательными задачами будем понимать «знаковую модель, речевая формулировка проблемной ситуации, не содержащая готовых образцов, а требующая новых решений, она способствует формированию активной, инициативной личности, с выраженными дискурсивно – креативными способностями» [4, с. 3].
Приведем познавательные задачи по одному из разделов математики «Зеркальные числа».
Зеркальными, или обращенными числами, называют числа, записанные одними и теми же цифрами, но в обратном порядке. Приведем примеры зеркальных чисел: 27853 и 35872; 100457 и 754001.
Приведенные ниже задачи можно предлагать ученикам 8-11 классов.
Задача 1. Двузначное число в сумме с зеркальным числом даёт полный квадрат. Найти все такие числа.
Решение.Искомое двузначное число равно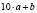 
. Зеркальное ему число равно 
.
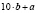Сумма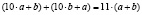 
может быть полным квадратом при условии 
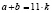, где k – полный квадрат. Поскольку 
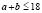, то k=1 и 
.
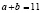Ответ: 29 и 92; 38 и 83; 47 и 74; 56 и 65.
Задача 2. Доказать, что разность двузначного числа и зеркальному ему кратна 9.
Доказательство. Пусть дано двузначное число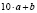 
. Вычтем из него зеркальное число 
; 
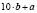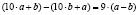. Видно, что это число кратно 9.
Задача 3. Произведение цифр двузначного числа в два раза больше суммы его цифр. Если от этого числа отнять 27, то получим число, зеркальное ему. Найти это число.
Решение. Пусть дано двузначное число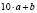 
. Зеркальное ему число имеет вид 
.
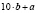Согласно условию задачи, можем составить систему:
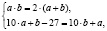
Откуда имеем
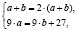
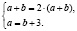
Подставив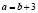 
в первое уравнение системы, получим 
, 
, 
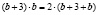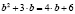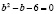, откуда b=3,
b = –2. Так как b – цифра, то она отрицательной быть не может. Окончательно имеем: b=3, a=6.
Ответ: 63.
Задача 4. Если переставить цифры некоторого числа, то получим число на 27 больше. Отняв от данного числа утроенную сумму его цифр, получим 24. Найти это число.
Решение. По условию задачи можем составить систему уравнений:
,
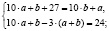
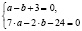откуда имеем a=6, b=9.
Ответ: 69.
Задача 5. Трехзначное число больше зеркального ему на 396, а сумма цифры сотен и цифры единиц данного числа в 1,5 раза больше цифры десятков. Найти это число.
Решение. Пусть дано трехзначное число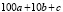 
. Зеркальное ему число имеет вид 
.
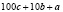Воспользуемся свойством: « Разность трехзначного числа и зеркального ему равна произведению разности цифр сотен и единиц этого число на 99».
Действительно:
.
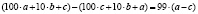Согласно свойству и условию задачи имеем: 396: 99=4.
Составим систему: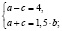 
откуда имеем
, 
, 
.
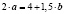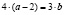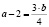Так как а – целое число, то b кратно 4
(и b ≤9).
При b =0 имеем: a=2, c=2 – ложное решение.
При b=4 имеем: a=5, c=1. Получим число 541.
При b=8 имеем: a=8, c=4. Получим число 884.
Ответ: 541, 884.
Задача 6. Трехзначное число относится к зеркальному как 7:4. Найти эти числа.
Решение. Разность двух зеркальных трехзначных чисел кратна 99 (см. задачу 5). Так как разность числителя и знаменателя дроби, представляющей отношение искомых чисел, равна 3 (7 – 4 = 3), то дробь эта сокращена, по меньшей мере, на 33. Умножив числитель и знаменатель дроби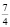 
на 33, получим пару искомых чисел: 
; 
.
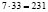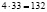Умножив полученные числа на 2 и на 3, получим еще две пары зеркальных чисел, отвечающих условию:
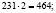
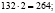
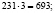
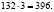
Ответ: 231 и 132; 462 и 264; 693 и 396.
Задача 7. Найти наименьшее трехзначное число, отношение которого к зеркальному равно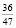 
.
Ответ: 324.
Задача 8. Найти трехзначное число, зная, что число его десятков есть среднее геометрическое чисел сотен и единиц, а если в его записи поменять местами цифры сотен и единиц и вычесть новое число из искомого, то разность будет равна 297.
Решение. Пусть дано число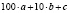 
.
Зеркальное ему число имеет вид
.
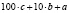Согласно свойству, описанному в задаче 5, и условию задачи имеем систему:
,
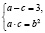откуда
, 
,
, 
,
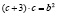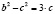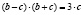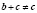поэтому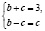 
, с=1, b=2, a=4.
Число имеет вид 421.
Ответ: 421.
Задача 9. Даны два двузначных зеркальных числа. Нашли разность этих чисел, затем поменяли местами цифры полученной разности и сложили два новых зеркальных числа. Найти полученную сумму.
Ответ: 99.
Задача 10. Сумма некоторого двузначного числа с его зеркальным равна 55, а произведение тех же чисел равно 736. Найти эти числа.
Ответ: 23 и 32.
Задача 11. Цифры некоторого семнадцатизначного числа записывают в обратном порядке. Полученное число складывается с первоначальным. Докажите, что хотя бы одна из цифр их суммы будет четной.
Доказательство. Рассуждения по поводу доказательства истинности высказанного предположения могут быть такими.
Записав цифры семнадцатизначного числа в обратном порядке, мы заметим, что девятая цифра числа останется на том же месте.
Если эта цифра задает четное число, то сумма двух четных чисел будет четной; если же эта цифра задает нечетное число, то сумма двух нечетных чисел также будет четной. Что и требовалось доказать.
Большое число поисковых задач читатель найдет в наших работах [1, 2].