Оптимизация количественных характеристик микроструктуры поверхностного слоя образцов из стали 110Г13Л, упрочнённых статико-импульсной обработкой (СИО), предполагает построение функциональных зависимостей входных характеристик от факторов эксперимента:
Y=F(x), (1)
где Y – оценка микроструктурных характеристик; x – вектор технологических факторов.
В работе выполнялось регрессионное моделирование, так как аналитическую форму зависимости (1) получить не предоставляется возможным из-за многофакторности процесса СИО. Функция (1) представлена в виде полинома второго порядка:
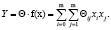(2)
где θ – вектор неизвестных параметров регрессионной модели; X – вектор факторов количественных характеристик микроструктуры; f(x) – вектор аргументов модели известных функций от факторов.
В качестве аргументов модели использованы аргументы полиномов первого и второго порядка. Дальнейшее повышение степени аргументов при исследовании закономерностей изменения микроструктуры в процессе СИО является не эффективным.
При построении регрессивных моделей вида (2.6) использованы планы, близкие к Д – оптимальным для обеспечения наибольшей точности оценок параметров модели и точности прогноза выходной характеристики в качестве факторов.
Значения факторов в плане определялось с учетом обеспечения реальных условий проектирования процесса. Оценка дисперсий воспроизводимости эксперимента определяются по следующей формуле:
S2в[y]=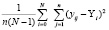
, (3)
где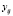 
– значение выходной характеристики в j-м опыте i-й серии; yi – среднее значение характеристик в i-й серии; n – число дублирующих опытов каждой серии; N – число серий опытов.
В каждой точке факторного пространства проводилась серия опытов, при этом число опытов в серии выбиралось не менее трех. Проверка предпосылок регрессионного анализа проводилась путем исследования однородности дисперсий воспроизводимости опытов в различных точках факторного пространства и соответствия распределения каждой выходной характеристики определенному закону распределения.
Построение регрессионной модели процесса СИО предполагает оценку 0 – параметров регрессионной модели и выбора ее аргументов определяемых вектором f(x):
0 = (FTF)-1 (FTY),
где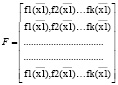 
–
матрица аргументов модели;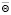 
– вектор оценок параметров модели; у – вектор значений выходной характеристики; 
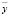– число оцениваемых параметров; 
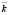– число оцениваемых параметров.
S2в{у}(FTF )-1 – является дисперсионной матрицей оценок параметров. Оценка дисперсий параметров определяется по диагональным элементам дисперсионной матрицы, а ее значимость – по критерию Стьюдента t:
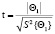; (4)
где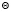 
– модуль значений i-гo параметра; 
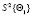– оценка дисперсий i-гo параметра.
Для подбора аргументов регрессионной модели использован шаговый метод. В модели вначале вводится аргумент, наиболее коррелированный с выходной характеристикой процесса, и оцениваются параметры модели. Затем поэтапно вводятся аргументы возможного набора с одновременной проверкой их значимости и удалением из модели незначимых аргументов. Информативность модели оценивается с помощью дисперсионного отношения:
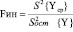, (5)
где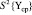 
– дисперсия отклонений фактических значений Y от их среднего значения Yср; S2{Y} – остаточная дисперсия отклонений предсказанных значений Y от их фактического значения Yср..
В качестве критерия адекватности регрессивной модели используется дисперсионное отношение
.
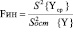Чем меньше значение (5), тем более обоснованным является предложение об адекватности модели. Обработка результатов экспериментов проводилась на ПЭВМ IBM PC в пакете программ Statistica 5.1.
Для оценки микроструктурных изменений при СИО в качестве параметров оптимизации были выбраны количественные характеристики микроструктуры: средний диаметр зерна dm, площадь сечения зерна S, среднее число зерен в 1 мм2 N, микротвердость Hµ. Рассматривая каждый параметр количественных характеристик необходимо учитывать их значимость при СИО.
Таким образом, в результате оптимизации определен основной критерий микроструктурных изменений, которым является средний диаметр зерна dm.