Экстраполятор трения пластины является базой для прогнозирования вязкостного сопротивления воды движению судна при его безотрывном обтекании. Аналитические экстраполяторы трения основаны на решениях уравнений движения жидкости при заданном профиле скорости в пограничном слое (ПС). При этом особенности движения жидкости в ламинарном подслое не учитываются [1, 2, 3, 4,…]. Кроме того, им присущи значительные погрешности в области средних чисел Рейнольдса. Для устранения этого недостатка часто применяют эмпирические зависимости [2, 5].
В работе разрабатываются экстраполяторы трения на основании решения уравнения движения жидкости в ламинарном подслое. В результате для пристеночной области движение жидкости описывается уравнением Лапласа [1]:
![]() . (1)
. (1)
Наиболее простым способом отыскания проекции скорости вдоль пластины ux является разделение переменных ![]() , с учетом которого решение уравнение определяется функцией вида:
, с учетом которого решение уравнение определяется функцией вида:
![]() . (2)
. (2)
Постоянные А1 и А2 определяются как:
![]() , (3)
, (3)
а именно из значенй касательных напряжений t00 на носике пластины (при х=0) и t0L – конце пластины (при х=L). Соответствующий закон изменения касательных напряжений по длине пластины примет вид
![]() . (4)
. (4)
В настоящее время [1,2,5,…] в пристеночной области ux описывается линейным законом ![]() , который удовлетворяет уравнению движения (1) и хорошо согласуется с экспериментально подтвержденным фактом [5], что
, который удовлетворяет уравнению движения (1) и хорошо согласуется с экспериментально подтвержденным фактом [5], что
![]() (5)
(5)
в области ламинарного подслоя и переходной зоне по толщине ПС при ![]() . По существу линейная зависимость для ux является частным тривиальным решением (1). Решение вида (2) более общим и не противоречит условию (5). Невозможность точного определения l из условия (5) не исключает возможности использования (4) для определения экстраполятора трения Cf для пластины. В этом случае l можно рассматривать как коэффициент, определяемый из условия согласования Cf с экспериментальными данными. Для этого случая выражение для экстраполятора будет, конечно, полуэмпирическим. Но используемые в настоящее время экстраполяторы, например, Прандтля-Шлихтинга,
. По существу линейная зависимость для ux является частным тривиальным решением (1). Решение вида (2) более общим и не противоречит условию (5). Невозможность точного определения l из условия (5) не исключает возможности использования (4) для определения экстраполятора трения Cf для пластины. В этом случае l можно рассматривать как коэффициент, определяемый из условия согласования Cf с экспериментальными данными. Для этого случая выражение для экстраполятора будет, конечно, полуэмпирическим. Но используемые в настоящее время экстраполяторы, например, Прандтля-Шлихтинга,
![]() (6)
(6)
так же являются полуэмпирическими, за счет корректировки выполненной Шлихтингом (по экспериментальным данным) [2] для решения полученного Прандтлем.
Перейдем к определению структурной зависимости для экстраполятора трения Cf0. Коэффициент трения пластины единичной ширины, длиной L определится в результате суммирования касательных напряжений по длине пластины,
![]() , (7)
, (7)
которая при ![]() и
и ![]() , дает соотношение:
, дает соотношение:
![]() . (8)
. (8)
Формула (8) кроме неопределенного члена lL содержит значения касательных напряжений t00 и t0L в носике и на конце пластины. Для их определения воспользуемся интегральным соотношением для ПС пластины [1]: ![]() , где
, где ![]() – толщина потери импульса ПС. Тогда структура формулы для экстраполятора трения Cf0 будет:
– толщина потери импульса ПС. Тогда структура формулы для экстраполятора трения Cf0 будет:
![]() , (9)
, (9)
что хорошо согласуется с известным решением для Cf0, полученным из интегрального соотношения [1]: ![]() . Относительная толщина на задней кромке пластины δL**/L, в настоящее время, может быть определена по одной из следующих формул [1, 2 ,5, …]:
. Относительная толщина на задней кромке пластины δL**/L, в настоящее время, может быть определена по одной из следующих формул [1, 2 ,5, …]:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
Коэффициенты a, n, m, b в них определяются из экспериментальных данных для пластины обобщённых Шлихтингом [2] и Г.Е. Павленко [7].
В результате обработки этих данных (с использованием метода наименьших квадратов и исключением явных промахов) получены следующие экстраполяторы трения:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Эти зависимости приведены на рис. 1, где (для сравнения) нанесены и другие экстраполяторы трения.
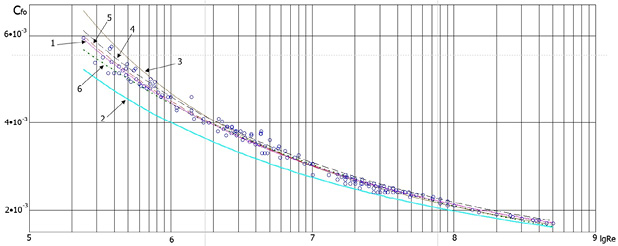
Экстраполятор трения. Обобщение экспериментальных данных (точки):1 – по формуле Прандтля-Шлихтинга ![]() ; 2 – по формуле А.Ф. Пустошного и В.М. Котловича
; 2 – по формуле А.Ф. Пустошного и В.М. Котловича ![]() ; 3 – по формуле МКОБ
; 3 – по формуле МКОБ ![]() ; 4, 5, 6 – по формулам (15), (13), (14) соответственно
; 4, 5, 6 – по формулам (15), (13), (14) соответственно
Анализируя результаты, приходим к следующим выводам:
– экстраполятор трения (13)
![]()
хорошо соответствует обобщенным экспериментальным данным (рисунок). При этом его значения численно близки к соответствующим значениям, полученным с использованием экстраполятора Прандтля-Шлихтинга. Но в тоже время, этот экстраполятор частично устраняет недостаток отмечаемый для формулы Прандтля-Шлихтинга – занижение значений трения при малых числах Рейнольдса;
– экстраполяторы трения (14) и (15) полученные исходя из более детального анализа характеристик ПС на пластине хорошо согласуются с экспериментальными данными в области чисел Рейнольдса Re>1•107, где все экстраполяторы практически идентичны. В области более малых Re экстраполятор (15) завышает значения Cf0, а (14) приводит к занижению этих значений. Таким образом, область их применения ограничена Re>1•107 при большей точности (14).



