Современная экономика столкнулась с крупнейшим за последние 70 лет экономическим кризисом. Основная причина экономического кризиса - неспособность современных субъектов экономической деятельности предсказать динамику хозяйственных процессов на основе существующих экономических моделей [1].
В экономике Российской Федерации существенную роль играют предприятия горнодобывающего комплекса. Прогнозирование динамики предприятий горнодобывающего комплекса является важной задачей для обеспечения устойчивого развития значительного числа регионов РФ и Российской Федерации в целом.
В настоящей работе нами предложена имитационная модель динамики основных хозяйственных потоков горнодобывающего предприятия. Модель представлена в дифференциальной форме. Модель позволяет осуществить прогнозирование качественной динамики основных показателей горнодобывающего предприятия: запасов сырьевого товара и прибыли от его реализации.
Рассмотрим хозяйственную систему горнодобывающего предприятия при следующих ограничениях: предприятие производит один вид товара, весь объем произведенного товара реализуется на рынке по рыночным ценам, кредитные ресурсы являются недоступными.
Рассмотрим распределение прибыли от продаж. Прибыль предприятия распределяется на инвестиционные цели и цели потребления:
Y = I + C (1)
В структуре инвестиционных расходов выделим инвестиции в воспроизводство геологической информации:
I = Ig + Io
где Ig - инвестиции в воспроизводство геологической информации;
Io - прочие инвестиции.
Следовательно, равенство (1) преобразуется в
Y = Ig + Io + C
Разделим и умножим на общую величину прибыли, получим равенство:
Y = ig*Y + io*Y + c*Y,
где ig - норма инвестиций в воспроизводство геологической информации (Ig : Y);
io - норма прочих инвестиций (Io : Y);
с - норма потребления (с*Y).
Общее изменение объема балансовых запасов ΔZ обозначим как
ΔZ = ΔZ+ - ΔZ-,
где ΔZ+ - прирост геологической информации о балансовых запасах руды, содержащей сырьевой товар в результате инвестиций в воспроизводство геологической информации,
ΔZ-, - уменьшение геологической информации о балансовых запасах руды, содержащей сырьевой товар в результате процесса производства сырьевого товара.
Для построения модели введем два технологических коэффициента системы:
α1 - коэффициент эффективности инвестиций в воспроизводство геологической информации. Коэффициент характеризует скорость преобразования инвестиций в воспроизводство геологической информации в объем запасов. α1 = ΔZ+ : ΔIg. Величина коэффициента зависит от технологии получения геологической информации.
α2 - коэффициент содержания сырьевого товара. Коэффициент характеризует норму извлечения сырьевого товара из руды. α2 = Δq : ΔZ-. Где q - объем извлеченного сырьевого товара. Величина коэффициента зависит от технологии извлечения сырьевого товара из руды и качества руды.
Введем показатель нормы вовлеченности запасов в процесс производства iex Норма вовлеченности запасов iex = ΔZ- : Z соответствует доле запасов сырьевого товара, используемых в процессе производства.
Кроме того, исходя из анализа параметров безубыточности определим критическую цену на сырьевой товар, при котором предприятие не получает прибыль pкрит.
Таким образом, для характеристики системы «запасы - прибыль» нами может быть использована одна из модификаций логистической функции - модель «хищник - жертва» [2].
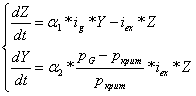(2)
где 
- прирост
геологической информации о балансовых запасах руды, содержащей сырьевой товар;
- прирост прибыли от
реализации добытого сырьевого товара,
pG - цена на сырьевой товар на мировом рынке.
Рост объема балансовых запасов руды, содержащей сырьевой товар в модели (2) определяется как частное функции инвестиций в воспроизводство геологической информации и функции потребления геологической информации в процессе производства сырьевого товара.
Величина дохода, полученного в процессе производства и реализации сырьевого товара, зависит от величины потребления геологической информации в процессе производства сырьевого товара.
В модели (2) присутствуют 2 параметра, прямо регулируемые руководящими органами хозяйствующего субъекта - ig и iex. Регулирование значения ig осуществляется путем распределения управляющими органами хозяйствующего субъекта потока прибыли на инвестиционные цели. Регулирование значения iex.осуществляется путем постановки плановых заданий в части объема производства сырьевого товара.
Технологические параметры α1 и α2 являются условно-постоянными вследствие медленного характера изменений в технологии получения геологической информации и технологии извлечения сырьевого товара. Параметр pкрит также является условно-постоянным в краткосрочном периоде.
Параметр pG - является быстроменяющейся величиной и управляющим параметром системы, в краткосрочном периоде. В среднесрочном и долгосрочном периоде управляющим параметром системы (2) является соотношение pG - pкрит. Именно от знака соотношения pG - pкрит зависит динамика объема запасов. При pG - pкрит > 0 в системе наблюдается экспоненциальный рост, а при pG - pкрит < 0 снижение запасов ресурса. Предельный случай pG - pкрит = 0 характеризует неустойчивое состояние консервативной системы.
Рассмотрим фазовый портрет модели более подробно.
Фазовая плоскость - координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы второго порядка [3].
Фазовый портрет - графическое отображение равновесного состояния системы при условиях, отвечающих координатам рассматриваемой точки на диаграмме.
Фазовый портрет системы (2) достаточно хорошо раскрыт в научной литературе вследствие того, что данная система является простейшей линейной системой дифференциальных уравнений, частным случаем линейной системы уравнений:
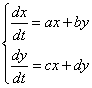(3)
Фазовый портрет системы зависит от значений параметров уравнения (3).
Решение системы (3) находится в форме [4]:
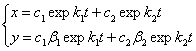
где β1, β2 - решения уравнения
(4)
k - решения уравнения
(5)
В случае модели вида (2) параметры соответственно равны
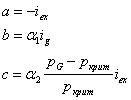
Для модели (2) и (3) качественные характеристики решения будут зависеть от типа собственных значений.
Исследуем динамику хозяйственной систему горнодобывающего предприятия при изменении соотношения управляемых параметров системы: нормы инвестиций в воспроизводство геологической информации (ig) и нормы вовлеченности запасов в процесс производства (iex).
Исследование предельных значений управляемых параметров имеет значение для прогнозирования границ возможной динамики хозяйственной системы горнодобывающего предприятия. Данный прогноз особенно важен в условиях экономического кризиса.
На основании определения норма инвестиций в воспроизводство геологической информации может изменяться от нуля, отсутствие инвестиций в воспроизводство геологической информации, до единицы, направление всей накопленной прибыли на инвестиции в воспроизводство геологической информации.
Пределы вариативности нормы вовлеченности запасов в процесс производства: от нуля, при отсутствии производства по добыче сырьевого товара до технически достижимого предела извлечения. В целях общности рассуждений рассмотрим максимально возможный верхний предел нормы вовлеченности запасов - единицу, другими словами, полное вовлечение запасов в процесс производства.
Таким образом, необходимо рассмотреть поведение системы (2) в крайних узлах квадранта iex, ig.
iex=0, ig=0. При данных условиях система (2) принимает вид:
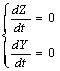(6)
Данная система соответствует состоянию множественного равновесия. Данное состояние является устойчивым. Характеристическое уравнение системы k2 = 0. Оба собственных значений системы (6) равны нулю. Любая точка на координатной плоскости ZY является точной равновесия. Все решения системы являются стационарными.
Экономическое условие равенства нулю показателей нормы вовлеченности запасов в процесс производства и нормы инвестиций в воспроизводство геологической информации - отсутствие хозяйственной деятельности горнодобывающим предприятием, что следует из начального предположения iex=0, ig=0.
iex=0, ig=1. При данных условиях система (2) принимает вид:
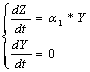(7)
Данная система соответствует состоянию множественного равновесия. Данное состояние является устойчивым. Характеристическое уравнение системы k2 = 0. Оба собственных значений системы (7) равны нулю. Любая точка на координатной плоскости ZY является точной равновесия. Все решения системы являются стационарными.
Система (7) описывает динамику предприятия, не имеющего производства. Экономически состояние отсутствия производства при наличии инвестиций в геологоразведку характерно для нового предприятия, которое ведет геологоразведочные работы, готовится к пуску основного производства.
iex=1, ig=0. При данных условиях система (2) принимает вид:
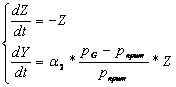(8)
Характеристическое уравнение системы
k2 + k =0. Собственные значения системы (8)
k1 = 0, k2 = -1
Система (2) в случае iex=1, ig=0 имеет множественные равновесия. Динамика системы (8) устойчива. Объем запасов стремится к нулю, объем доходов стремится к равновесному значению. Система (8) описывает затухающую динамику экономической активности.
Решением системы (8) является система уравнений:
При t→∞ система преобразуется к виду
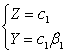
Найдем β1 из уравнения (4) 
. Таким образом, соотношение Z и Y позволит найти
стационарное решение системы (8). Стационарные решение системы (8) является
уравнение 
.
Экономически в случае максимальных объемов извлечения запасов и отсутствия инвестиций в геологоразведку хозяйственная система горнодобывающего предприятия сокращает хозяйственную деятельность. Система (8) характеризует динамику горнодобывающего предприятия на поздних стадиях жизненного цикла данного горнодобывающего предприятия.
iex=1, ig=1. При данных условиях система (2) принимает вид:
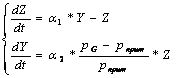(9)
Корни характеристического уравнения системы (9) зависят от знака соотношения pG - pкрит.
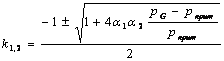
В отличие от динамики систем (6 - 8) система (9) не является вырожденной, и динамика данной системы зависит от динамики системы (2).
Таким образом, в модели (2) параметр iex представляет собой акселератор доходов. При
iex = 0 (случай остановки производства) в системе (2)
наблюдается стационарное равновесие, прекращается эволюция.
Параметр ig представляет собой акселератор запасов. При ig = 0 в системе (2) наблюдается затухающая эволюция к стационарному равновесному состоянию.
Модель (2) является достаточно грубым приближением реальной динамики хозяйственной системы горнодобывающего предприятия. В отдельных случаях необходимо учитывать виляние на хозяйственную систему горнодобывающего предприятия возможности привлечения заемного капитала.
Одним из наиболее важных частных случаев существенности учета потока заемного капитала для характеристики динамки системы горнодобывающего предприятия является процесс организации нового производства. Новое производство, как правило, организуется на заемный капитал. Другим важным случаем, при котором имеет значение учет влияния потока заемного капитала, является процесс инвестиций в геологическую информацию о новых месторождениях горнорудного сырья.
Модель (2) апробирована на примере хозяйственной системы ОАО «Покровский рудник». Модель (2) показала хорошее качество имитации динамики основных параметров ОАО «Покровский рудник» за 2004 - 2008 годы.
СПИСОК ЛИМТЕРАТУРЫ
1. Занг Вэй-Бин Синергетическая экономика: Время и перемены в нелинейной экономической теории: Пер. с англ.: М.: Мир, 1999.- C. 177
2. Пугачева Е.Г., Соловьенко К.Н. Самоорганизация социально - экономических систем - Иркутск: Изд-во БГУЭП, 2003. - C. 86
3. Андронов А.А. Теория колебаний / А.А.Андронов, А.А. Витт, С.Э. Хайкин - М.: Государственное издательство физико-математической литературы, 1959. - C. 38
4. Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 2 - М.: Наука, Главная редакция физико-математической литературы, 1985.- C. 116