Предлагаемый метод разложения фазового портрета [4] рассматриваемого временного ряда на квазициклы состоит из трех этапов: 1) выбор размерности p фазового пространства 
; 2) построение фазовой траектории (фазового портрета) путем соединения отрезками кривых соседних точек 
, 
; 
; 3) разложение этого портрета на квазициклы.
Для различных экономических временных рядов достаточным является построение фазового портрета в фазовом пространстве размерности 
. В качестве иллюстративного примера использования инструментария фазового анализа рассмотрен временной ряд помесячного количества заболевших ОРЗ детей за период февраль 1996 г. - ноябрь 2006 г.
Рассмотрим этот фазовый портрет в виде траектории (см. рис.1), т.е. последовательности точек, в которой каждая соседняя пара соединена звеном, т.е. отрезком или кривой. В этой траектории выделяем также ее части, которые называются термином «квазициклы». Определение квазицикла в определенном смысле близко к определению цикла. Различие между этими двумя понятиями состоит в том, что начальная и конечная точки квазицикла не обязательно должны совпадать. Конечная точка квазицикла определяется ее вхождением в окрестность начальной точки. При этом допускается самопересечение начального и конечного звеньев квазицикла.
Рис. 1. Фазовый портрет временного ряда помесячного количества заболевших ОРЗ детей
В целом фазовый портрет рассматриваемого временного ряда Z состоит из последовательности 16-ти непересекающихся квазициклов Qr, r = 1,2,...,16, размерность которых в типичном случае колеблется от 4 до 12. Эти квазициклы обозначаем через Qr, их длину - соответственно через nr, последовательно номеруя индексом r = 1,2,...,16; 
. Длины этих квазициклов получили значения 
, 
, 
, 
, 
, 
, 
, 
, 
. Для наглядности на рис. 2 представлена гистограмма частот в распределении этих длин.
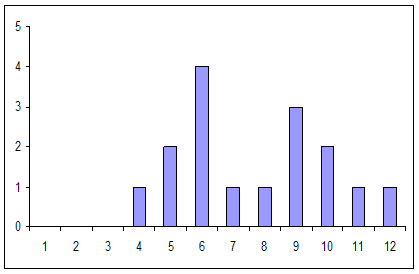
Рис. 2. Гистограмма частот длин квазициклов фазового портрета на рис. 1
С точки зрения обеспеченности лечебного заведения необходимыми ресурсами (медперсонал, диагностическая аппаратура и т.д.) представляет интерес вопрос о том, существует ли для рассматриваемого временного ряда вида сезонная цикличность. Результатом настоящего исследования является выявленная квазицикличность во временном ряде помесячного количества заболевших ОРЗ детей в г.Черкесске. Квазициклы имеют длину от 6 до 9 уровней, что соответствует календарно интервалу от 7 до 10 месяцев.
Работа выполнена при поддержке РФФИ, проект №06-01-00020а
СПИСОК ЛИТЕРАТУРЫ:
- Шустер Г. Детерминированный хаос: Введение. - М.: Мир, 1988. - 240 с.
- Сергеева Л.Н. Моделирование поведения экономических систем методами нелинейной динамики (теории хаоса). - Запорожье: ЗГУ, 2002. - 227 с.
- Gilmore C.G. A new test for chaos //Journal of economic behavior and organization, №22, 1993. - P. 209-237.
- Петерс Э. Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка,- М.: Мир, 2000. - 333 с.