Наличие возмущающих воздействий, обусловленных изменением нагрузки, взаимосвязанностью и взаимовлиянием контуров управления сложных многомерных систем, которые функционируют в различных эксплуатационных режимах, а также естественное изменение во времени характеристик объекта управления и параметров системы управления, приводят к тому, что задающие воздействия и управляемые величины носят случайный характер. Природа наблюдаемых процессов, происходящих в системах, является причиной того, что результаты измерений искажены помехами и содержат инструментальные и методические погрешности. В подобного типа системах требуется сложная обработка измерительной информации. Основной подход к решению этой задачи заключается в применении алгоритмов фильтрации.
В настоящее время наиболее полно решены проблемы синтеза алгоритмов фильтрации для линейных систем при аддитивных гауссовских помехах с помощью фильтров Калмана [1]. В практике научных и инженерных расчетов используются также субоптимальные алгоритмы оценивания нелинейных непрерывных марковских процессов. Применение этих методов в реальном масштабе времени ограничено. Уравнения, положенные в основу решения задач фильтрации, сложны для практической реализации и предъявляют повышенные требованиям к вычислительным ресурсам системы управления. Кроме того, ограниченность применения указанных подходов обусловлена нестационарностью процессов, имеющие место в условиях эксплуатации систем управления. Поэтому с целью улучшения показателей качества управления требуется разработка методов, алгоритмов и средств, обеспечивающих повышение достоверности оценки управляемой величины на фоне помех.
Цель работы
Случайный характер измерительных сигналов обуславливает применение процедуры статистической обработки результатов измерений, основой которой является операция усреднения, осуществляемая либо усреднением по времени, либо усреднением в пространстве реализаций. Это приводит к необходимости выделения таких составляющих погрешности как статистическая погрешность и погрешность, обусловленная неадекватностью алгоритма обработки реальному случайному процессу.
В соответствии со сложившейся практикой статистические погрешности обусловлены конечностью объема данных о мгновенных значениях наблюдаемых величин. Адекватность операторов обработки результатов измерений достигается рассмотрением эргодических стационарных случайных процессов.
В действительности практический интерес представляет обработка нестационарных случайных процессов по одной реализации, поскольку модель нестационарного процесса является наиболее адекватной широкому кругу явлений. При исследовании случайных процессов свойство эргодичности установлено лишь для некоторых видов нестационарных процессов, в остальных случаях оно постулируется, тем самым уже априори результаты обработки будут содержать ошибку.
Встречаемые в инженерной практике процессы часто можно представить в виде аддитивной, мультипликативной или аддитивно-мультипликативной модели. Если имеющиеся экспериментальные данные позволяют установить вид нестационарного процесса, то оценить его параметры можно по одной реализации. Во многих случаях операции центрирования и нормирования преобразуют исследуемый исходных процесс к стационарному, что позволяет далее эффективно использовать известные методы анализа стационарных процессов.
Один из возможных путей повышения точности выделения полезного сигнала является разработка алгоритмов обработки измерительной информации в соответствии с классом процесса (стационарный - нестационарный процесс), вида процесса (аддитивный, мультипликативный или аддитивно - мультипликативный) и типа детерминированной составляющей.
Предлагаемый метод решения проблемы
В настоящее время для определения класса случайного процесса предпочтение отдается непараметрическим критериям [2]. Авторами был проведен анализ чувствительности непараметрических критериев к различным видам моделей нестационарных процессов, типу и параметрам детерминированных составляющих [3, 4]. Для определения класса случайного процесса предлагается совместное использование критерия инверсий или критериев, основанных на ранговой корреляции, критерия рекордных точек, теста Бокса-Пирса.
Исследования показали, что при обработке коротких временных рядов не следует слишком доверять числовым характеристикам степени достоверности выводов по непараметрическим критериям. Статистические методы обработки измерительной информации необходимо дополнять другими методами анализа. В данном случае предлагается вычислять показатель Херста [5], по значению которого с определенной степенью достоверности можно судить о классе процесса и виде детерминированной составляющей.
В отличии от существующей практики предлагается процедура обработки случайных процессов, включающая пять этапов. Структура информационной системы анализа случайного процесса в соответствии с предлагаемой процедурой представлена на рис.1.
Целью первого этапа (блок 3) является определение класса случайного процесса. Задача второго этапа заключается в определении вида процесса (блок 4). На третьем этапе процедуры обработки выявляется тип детерминированной составляющей случайного процесса (блок 5).
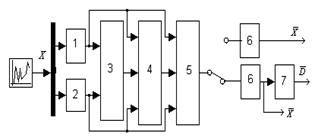
Рисунок 1. Структура информационной системы анализа случайного процесса:
![]() - оценка математического ожидания,
- оценка математического ожидания, ![]() - оценка дисперсии.
- оценка дисперсии.
В структуру информационной системы анализа включены блок расчета числовых характеристик непараметрических критериев (блок 1) и блок вычисления показателя Херста (блок 2).
Аддитивная модель характеризует процессы нестационарные по математическому ожиданию, которые при центрировании могут быть преобразованы к стационарным. Операция центрирования выполняется в шестом блоке. В данном блоке реализован алгоритм скользящего среднего, который одновременно с вычислением оценок математического ожидания допускает выполнение операции центрирования и не предъявляет никаких требований к закону изменения математического ожидания и дисперсии исследуемого процесса. Точность выполнения операции центрирования зависит от параметров наблюдаемого процесса, интервала дискретизации и окна сглаживания. На этом этапе выполняется адаптивная процедура по выбору окна сглаживания.
Последний этап обработки случайного процесса (блок 7) реализуется только для мультипликативной и аддитивно-мультипликативной моделей случайных процессов и заключается в выполнении процедуры нормирования.
Выводы
В инженерной практике случайные процессы занимают значительное место. В отличии от существующей практики предложен новый подход к решению задачи обработки информации, предусматривающий наличие процедур определения класса, вида процесса и типа детерминированной составляющей случайного процесса. Рассматриваемый подход позволяет повысить точностные характеристики подсистем измерения, контроля и управления, входящих в состав информационно-управляющих комплексов сложных систем.
СПИСОК ЛИТЕРАТУРЫ
- Казаков И.Е. Статистическая теория систем управления в пространстве состояний. - М.: Наука, 1975. - 432 с.
- Кендалл М. Дж., Стьюарт А. - Многомерный статистический анализ и временные ряды. Пер. с англ. - М.: Наука, 1976. - 736 с.
- Прохоренков А.М., Качала Н.М. Идентификация динамических характеристик случайных процессов// Труды II международной конференции «Идентификация систем и задачи управления» SICPRO´2000. Москва, 26-28 сентября 2000. - М.: Институт проблем управления им. В.А. Трапезникова РАН, 2000. С. 1251-1261.
- Prokhorenkov A.M. Methods for identification of random process characteristics in information processing systems// IEEE Transactions on Instrumentation and Measurement, 2002, vol. 51, no. 3, pp. 492-496.
- Федер Е. Фракталы. Пер. с англ. - М.: Мир, 1991. - 254 с.



