Проблема восстановления вычислительного процесса (задания) вследствие отказа программно-аппаратного обеспечения актуальна при решении больших фундаментальных и прикладных задач в разнородных распределенных вычислительных средах, в том числе в Grid различного назначения. Существуют различные подходы к решению данной проблемы [8].
В частности, широко применяемым на практике подходом к перезапуску заданий является механизм контрольных точек [7]. Однако формирование пользовательских контрольных точек в узле Grid, в котором выполняется вычислительный процесс, не позволяет произвести рестарт в случае отказа самого узла. Создание же системных контрольных точек на уровне операционной системы, обеспечивающих перенос задания в другие узлы, влечет существенные накладные расходы и поддерживается далеко не всеми системами управления Grid.
В статье рассматривается алгоритм восстановления вычислительного процесса после его отказа в Grid, где управление вычислениями реализуется мультиагентной системой [3]. В отличие от других подходов к управлению вычислениями и обеспечению их надежности [9, 10], наш подход базируется на реализации адаптивного мульти-сценарного алгоритма решения данной задачи, интегрирующего ряд эффективных и надежных алгоритмов взаимодействия агентов.
Иерархическая структура мультиагентной системы может включать два или более уровней функционирования агентов. На каждом уровне могут функционировать агенты, играющие различные роли и соответственно выполняющие различные функции. Роли агентов могут быть постоянными и временными, возникающими в дискретные моменты времени в связи с необходимостью организации коллективного взаимодействия. Уровни иерархии агентов отличаются объемом знаний агентов – агенты более высокого уровня иерархии обладают большим объемом знаний по сравнению с агентами более низкого уровня иерархии и, кроме того, могут обращаться к агентам любого ниже лежащего уровня с запросом на получение локальных знаний этих агентов. На каждом уровне иерархии агенты могут объединяться в виртуальные сообщества, кооперироваться и конкурировать в рамках этих сообществ.
Вычислительная модель
Пусть Z, F и M – это множество параметров, операций и программных модулей вычислительной модели предметной области. Операции из F определяют отношения вычислимости на множестве параметров Z. Каждая операция fi ∈ F реализуется модулем mj ∈ M, где 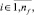
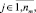 nf – число операций; nm – число модулей. Один модуль может реализовывать несколько операций. С каждой операцией fi связано два множества параметров
nf – число операций; nm – число модулей. Один модуль может реализовывать несколько операций. С каждой операцией fi связано два множества параметров 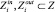 . Множество
. Множество 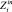 определяет параметры, значения которых необходимо задать, чтобы получить значения параметров, представленных множеством
определяет параметры, значения которых необходимо задать, чтобы получить значения параметров, представленных множеством 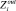 . Множества
. Множества 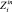 и
и 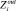 представляют соответственно множества входных и выходных параметров модуля mj, реализующего операцию fi.
представляют соответственно множества входных и выходных параметров модуля mj, реализующего операцию fi.
Постановки задач могут формулироваться в полной или сокращенной (процедурной или непроцедурной) форме. По сформулированной постановке задачи строится схема решения задачи на основе сочетания волновых и переборных методов планирования вычислений [4]. В общем случае в вычислительной модели предметной области может существовать множество S эквивалентных схем решения задачи. Схема s ∈ S определяет, какие операции и в какой последовательности должны быть выполнены для решения задачи.
Полная постановка задачи sf, совпадающая со схемой s, определяется структурой 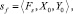 где Fs ⊂ F – множество операций, которые нужно выполнить для решения задачи; X0 ⊂ Z – множество исходных параметров, значения которых заданы; Y0 ⊂ Z – множество целевых параметров, значения которых нужно вычислить.
где Fs ⊂ F – множество операций, которые нужно выполнить для решения задачи; X0 ⊂ Z – множество исходных параметров, значения которых заданы; Y0 ⊂ Z – множество целевых параметров, значения которых нужно вычислить.
Остаточная схема решения задачи
Пусть c(P, X, Y) – вычислитель, выполняющий программы из множества P, где X – множество параметров программ из P, значения которых вычислены; Y – множество параметров программ из P, значения которых нужно вычислить. Тогда, согласно А.П. Ершову [6], программа px(Y) ∈ P называется остаточной программой (проекцией p на x) такой, что px(y) = p(x, y), x ⊂ X, y ⊂ Y.
Пусть s ∈ P и вычислителем выполнено множество Fr ⊂ Fs операций. Тогда, остаточной схемой sx(y) ∈ P решения задачи называется проекция s на x, где Z ⊆ X, 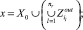
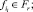
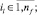
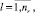 nr – число выполненных операций схемы s,
nr – число выполненных операций схемы s, 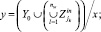
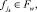 Fw – множество невыполненных операций схемы s,
Fw – множество невыполненных операций схемы s, 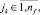
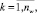 nw – число невыполненных операций схемы s.
nw – число невыполненных операций схемы s.
Сценарии обработки отказов
Виды, признаки и причины отказов объектов вычислительной среды с различной степенью их детализации описаны в [1]. Мы рассматриваем следующие объекты среды: узлы, агенты и модули.
Соответственно, мы учитываем следующие отказы: отказ узла (узел находится в нерабочем состоянии); отказ агента (агент не отвечает в течение установленного периода времени); отказ модуля (аварийное завершение выполнения модуля). Эти отказы обобщают различные причины и признаки неисправностей рассматриваемых объектов. Каждый отказ приводит к необходимости перезапуска модуля схемы решения задачи или выполнения другого модуля.
Рисунок иллюстрирует сценарии обработки перечисленных выше отказов.
Модуль может быть выполнен другим агентом в случае всех трех отказов. Кроме того, при отказе узла модуль может быть выполнен также в резервном узле. Дополнительно, при отказе модуля выполнявшейся схемы решения задачи может быть выполнен модуль эквивалентной схемы решения задачи.
Есть три возможных варианта назначения агента для выполнения модуля:
– централизованное (директивное) назначение модуля другому агенту, имеющему возможность выполнить данный модуль, координатором выполнения схемы решения задачи;
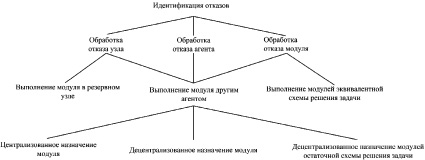
Сценарии обработки отказов
– децентрализованное назначение модуля путем проведения торгов между агентами, которые могут выполнить данный модуль;
– децентрализованное назначение модулей остаточной схемы решения задачи путем проведения торгов между агентами, которые могут принять участие в выполнении модулей остаточной схемы.
Состав виртуального сообщества агентов, выполняющих схему решения задачи, обновляется после назначения новых агентов для выполнения модулей. Выделение ресурсов агентами осуществляется с учетом различий вычислительных характеристик узлов Grid при реализации многоуровневого параллелизма алгоритма решения задачи.
Алгоритм
Пусть Z* – это множество простых и составных логических параметров, принимающих значения из множества {0, 1, θ}, Z* ⊂ Z. Составной параметр реализует логическое выражение, сформированное из простых параметров и логических операторов. Составной параметр не определен, если не определен хотя бы один из его простых параметров. Обозначим через A и PR множество действий по обработке отказов и множество продукций, определяющих правила выбора действий: 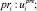 zj ⇒ ak;
zj ⇒ ak; 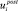 , где предусловие продукции определяется как
, где предусловие продукции определяется как
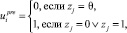
zj ⇒ ak - ядро продукции, интерпретируемое как выбор действия ak ∈ A по обработке отказа, zj ∈ Z*, 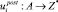 – постусловие продукции. Каждая продукция имеет приоритет.
– постусловие продукции. Каждая продукция имеет приоритет.
Связи между продукциями и логическими параметрами в левых частях их ядер представлены булевой матрицей B, размерности np×nz, где np – число продукций; nz – число логических параметров. Элемент матрицы b i,j = 1 означает, что продукция pri использует параметр zj. Связи между продукциями и действиями представлены булевой матрицей R, размерности np×na, где na – число действий. Элемент матрицы ri,k = 1 означает, что продукция pri описывает правило выполнения действия ak. Зависимости между действиями представим булевой матрицей D размерности na×na. Элемент матрицы 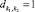 означает, что действие
означает, что действие 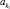 зависит от действия
зависит от действия 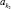 .
.
Адаптивный алгоритм восстановления вычислительного процесса включает следующие основные этапы.
1. Обработка предусловий 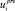 продукций pri,
продукций pri, 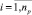 .
.
2. Если 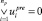 , то задача неразрешима. Переход на шаг 10.
, то задача неразрешима. Переход на шаг 10.
3. Формирование списка продукций 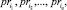 ядра которых могут быть выполнены:
ядра которых могут быть выполнены: 
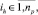
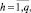
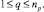
4. Вычисление левых частей 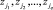 ядер продукций
ядер продукций 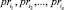 :
: 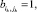
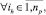
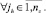
5. Если 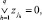 то задача неразрешима. Переход на шаг 10.
то задача неразрешима. Переход на шаг 10.
6. Выбор действия ak:rn,k = 1, где 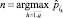 ,
, 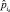 – приоритет продукции
– приоритет продукции 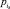 .
.
7. Выполнение действия ak и обработка постусловия продукции pn.
8. Если 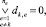 то задача решена. Переход на шаг 10.
то задача решена. Переход на шаг 10.
9. Конкретизация вычислительной модели: A = A\{ak}, PR = PR\{pn}. Переход на шаг 1.
10. Завершение работы алгоритма.
Обработка предусловий продукций обеспечивает адаптацию работы алгоритма к текущему состоянию Grid и выбор наиболее подходящего сценария действий по устранению отказа. Алгоритмы, применяемые при выполнении децентрализованного назначения модулей, идентификации отказов и резервирования узлов, рассмотрены в [3, 5, 7].
Модель функционирования агентов
Алгоритмы функционирования агентов разработаны на основе конечно-автоматной модели в соответствии со спецификой действий, выполняемых этими агентами в системе. Модель имеет следующий вид
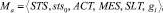
где STS – множество состояний агента; sts0 ∈ STS – начальное состояние агента; ACT – множество действий, совершаемых агентом, которое включает подмножество локальных действий ACTlocl ⊂ ACT, а также подмножества коммуникационных взаимодействий с другими агентами: отправки сообщений ACTsend ⊂ ACT и приема сообщений ACTrecv ⊂ ACT; MES – множество входных и выходных сообщений агента, SLT – система логического времени для датировки событий мультиагентной системы, gl – логическая функция переходов из одного состояния в другое в результате действий, совершаемых агентом.
Система логического времени SLT представлена следующей структурой:
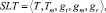
где T – область значений логического времени; Tm – область значений временных маркеров датировки сообщений, Tm ⊆ T; gt – функция логического времени; gm – функция датировки сообщений; gr – функция сравнения значений логического времени. Система логического времени использует векторные логические часы, в которых число компонент вектора времени равно числу агентов виртуального сообщества.
Реализация агентов осуществляется с помощью Java Agent DEvelopment framework (JADE) [2]. Сообщения создаются с помощью языка Agent Communication Language [2]. Очередь сообщений агента в JADE формируется в порядке поступления сообщений на физическом уровне. Этот порядок может не соответствовать логической обусловленности событий мультиагентной системы. Причинами такого несоответствия могут быть как рассинхронизация физических часов агентов, так и задержка передачи сообщений в коммуникационных каналах связи.
Система логического времени позволяет определить отношение частичного порядка на множестве событий мультиагентной системы с учетом их обусловленности. Использование функции датировки сообщений обеспечивает их обработку в установленной логической последовательности, а не в произвольном порядке поступления их в очередь.
Для обеспечения надежности системы передачи сообщений мы используем протокол с двумя сообщениями [8], который может приводить к дублированию, но не допускает потери информации, так как все сообщения содержат временные маркеры датировки сообщений и идентификаторы виртуальных сообществ агентов.
Заключение
В статье представлен адаптивный мультиагентный алгоритм, предназначенный для перераспределения вычислительных ресурсов Grid при возобновлении процесса решения задачи в рамках модульной системы программирования. Функционирование данного алгоритма базируется на методах конкретизирующего программирования для построения и выполнения остаточной схемы решения задачи. Предложена конечно-автоматная модель поведения агента, использующая систему логического времени и надежный протокол обмена сообщениями.
Исследование выполнено при финансовой поддержке РФФИ, проекты № 15-29-07955-офи_м и № 16-07-00931-а, а также при частичной финансовой поддержке Совета по грантам Президента Российской Федерации для государственной поддержки ведущих научных школ Российской Федерации (НШ-8081.2016.9).
Библиографическая ссылка
Феоктистов А.Г., Костромин Р.О. МУЛЬТИАГЕНТНЫЙ АЛГОРИТМ ПЕРЕРАСПРЕДЕЛЕНИЯ ВЫЧИСЛИТЕЛЬНЫХ РЕСУРСОВ ДЛЯ ОСТАТОЧНОЙ СХЕМЫ РЕШЕНИЯ ЗАДАЧИ В GRID // Современные наукоемкие технологии. 2016. № 9-2. С. 244-248;URL: https://top-technologies.ru/ru/article/view?id=36211 (дата обращения: 26.04.2025).



